State the principle of potentiometer. With the help of circuit diagram, describe a method to find the internal resistance of a primary cell.
Step-by-Step Solution
Step 1: State the Principle of Potentiometer
The principle of a potentiometer states that the potential drop across a segment of a wire of uniform cross-section carrying a constant current is directly proportional to the length of that segment. Mathematically, this can be expressed as:
\( V \propto L \)
where \( V \) is the potential drop and \( L \) is the length of the wire segment.
Step 2: Draw the Circuit Diagram
To find the internal resistance of a primary cell using a potentiometer, we need to set up a circuit. The circuit consists of:
- A primary cell (with EMF \( E \) and internal resistance \( r \))
- An external resistance \( R \)
- A rheostat
- A potentiometer wire (PQ)
- A galvanometer
- A jockey
The circuit diagram can be represented as follows:
±−−(E)−−−(R)−−−+|||∣||(G)(P−Q)|∣±−−−−−−−−−−−−−−+
Step 3: Set Up the Circuit
1. Connect the primary cell in series with the external resistance \( R \).
2. Connect the potentiometer wire (PQ) across the terminals of the cell.
3. Connect a galvanometer and a jockey to measure the potential difference across the wire.
Step 4: Measure Balancing Lengths
1. Close the switch and adjust the jockey along the potentiometer wire until the galvanometer shows zero deflection. This gives the balancing length \( L_1 \).
2. Open the switch to disconnect the cell and measure the balancing length again, which will be \( L_2 \).
Step 5: Apply the Formula
Using the relationship between EMF, potential difference, and the lengths measured:
- The EMF of the cell can be expressed as:
\( E = k \cdot L_1 \)
- The potential difference across the external resistance when the switch is open can be expressed as:
\( V = k \cdot L_2 \)
where \( k \) is the potential gradient along the wire.
Step 6: Calculate Internal Resistance
From Ohm's law, we know:
\( I = \frac{E}{R + r} \)
Rearranging gives:
\( I \cdot R = E - I \cdot r \)
Substituting \( I \) into the equation leads to:
\( r = R \cdot \frac{L_1 - L_2}{L_2} \)
Thus, the internal resistance \( r \) of the cell is given by:
\( r = R \cdot \frac{L_1 - L_2}{L_2} \)
The principle of a potentiometer states that the potential drop across a segment of a wire of uniform cross-section carrying a constant current is directly proportional to the length of that segment. Mathematically, this can be expressed as:
\( V \propto L \)
where \( V \) is the potential drop and \( L \) is the length of the wire segment.
To find the internal resistance of a primary cell using a potentiometer, we need to set up a circuit. The circuit consists of:
- A primary cell (with EMF \( E \) and internal resistance \( r \))
- An external resistance \( R \)
- A rheostat
- A potentiometer wire (PQ)
- A galvanometer
- A jockey
1. Connect the primary cell in series with the external resistance \( R \).
2. Connect the potentiometer wire (PQ) across the terminals of the cell.
3. Connect a galvanometer and a jockey to measure the potential difference across the wire.
1. Close the switch and adjust the jockey along the potentiometer wire until the galvanometer shows zero deflection. This gives the balancing length \( L_1 \).
2. Open the switch to disconnect the cell and measure the balancing length again, which will be \( L_2 \).
Using the relationship between EMF, potential difference, and the lengths measured:
- The EMF of the cell can be expressed as:
\( E = k \cdot L_1 \)
- The potential difference across the external resistance when the switch is open can be expressed as:
\( V = k \cdot L_2 \)
where \( k \) is the potential gradient along the wire.
From Ohm's law, we know:
\( I = \frac{E}{R + r} \)
Rearranging gives:
\( I \cdot R = E - I \cdot r \)
Substituting \( I \) into the equation leads to:
\( r = R \cdot \frac{L_1 - L_2}{L_2} \)
\( r = R \cdot \frac{L_1 - L_2}{L_2} \)
Topper's Solved these Questions
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set- II]4videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set-III]3videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET-III, DELHI BOARD4videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
Internal resistance of a cell depends on
View SolutionState the working principle of potentiometer. With the help of the circuit diagram, explain how a potentiometer is used to compare the emf's of two primay cells. Obtain the required expression used for comparing the emfs. Write two possible causes for one sided deflection in a potentiometer experiment.
View SolutionWrite the principle of working of a potentiometer. Describe briefly, with the help of a circuit diagram, how a potentiometer is used to determine the internal resistance of a given cell.
View SolutionWith the help of a suitable diagram, describe the structure and function of a neuron.
View SolutionState the underlying princeiple of mater bridge. Draw the circuit diagram and explain how the unknown resistance of a conductor can be determined by this method.
View SolutionWith the help of suitable diagrams, describe :
(a) Binary fission in plants (b) Budding in Yeast cellView SolutionUsing the principle of Wheatstone Bridge, describe the method to determine the specific resistance of a wire in the laboratory. Draw the circuit diagram and write the formula used. Write any two important precautions you would observe while performing the experiment.
View SolutionThe e.m.f. of a primary cell is 2V, when it is shorted then it gives a current of 4A. Calculate internal resistance of primary cell.
View SolutionA potentiometer circuit with potentiometer wire 10 m long, and an ideal main battery of e.m.f 8 V, has been set up for finding the internal resistance of a given cell. When the resistance R, connected across the given cell, has values of (i) infinity, (ii) 10 omega , the balancing lengths, on the potentiometer wire are found to be 2.4 m and x respectively. If the internal resistance of the cell is 2 ω, the value of x is
View SolutionFor the given circuit,
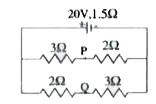
If internal resistance of cell is 1.5Ω, thenView Solution
