If χ stands for the magnetic susceptibility of a given material, identify the class of material for which
(i)−1≥χ<0
(ii) 0χ<∈(∈stands for a small positive number)
To solve the problem, we need to identify the classes of materials based on their magnetic susceptibility (χ).
1. Understanding Magnetic Susceptibility (χ):
- Magnetic susceptibility (χ) is a dimensionless quantity that indicates how much a material will become magnetized in an applied magnetic field.
- The value of χ can be negative, zero, or positive.
2. Analyzing the First Condition:
- The first condition given is:
−1≥χ<0
- This means that the magnetic susceptibility is less than zero and can be equal to -1 but cannot exceed it.
- Materials that have a negative susceptibility are known as diamagnetic materials. These materials are characterized by their tendency to be repelled by a magnetic field.
3. Conclusion for the First Condition:
- Therefore, for the condition −1≥χ<0, the class of material is diamagnetic.
4. Analyzing the Second Condition:
- The second condition given is:
0<χ<ϵ
- Here, ε stands for a small positive number, meaning that the susceptibility is positive but very small.
- Materials that have a small positive susceptibility are known as paramagnetic materials. These materials are weakly attracted by a magnetic field.
5. Conclusion for the Second Condition:
- Therefore, for the condition 0<χ<ϵ, the class of material is paramagnetic.
Final Answer:
(i) The class of material for −1≥χ<0 is diamagnetic.
(ii) The class of material for 0<χ<ϵ is paramagnetic.
---
- Magnetic susceptibility (χ) is a dimensionless quantity that indicates how much a material will become magnetized in an applied magnetic field.
- The value of χ can be negative, zero, or positive.
- The first condition given is:
−1≥χ<0
- This means that the magnetic susceptibility is less than zero and can be equal to -1 but cannot exceed it.
- Materials that have a negative susceptibility are known as diamagnetic materials. These materials are characterized by their tendency to be repelled by a magnetic field.
- Therefore, for the condition −1≥χ<0, the class of material is diamagnetic.
- The second condition given is:
0<χ<ϵ
- Here, ε stands for a small positive number, meaning that the susceptibility is positive but very small.
- Materials that have a small positive susceptibility are known as paramagnetic materials. These materials are weakly attracted by a magnetic field.
- Therefore, for the condition 0<χ<ϵ, the class of material is paramagnetic.
(i) The class of material for −1≥χ<0 is diamagnetic.
(ii) The class of material for 0<χ<ϵ is paramagnetic.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set- II]
4 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set-III]
3 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET-III, DELHI BOARD
4 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
The variation of magnetic susceptibility (χ) with absolute temperature T for a ferromagnetic material is
View SolutionThe susceptibility of a magnetic material is 0.9853. Identify the type of magnetic material. Draw the modification of the field pattern on keeping a piece of this material in a uniform magnetic field.
View Solution
Knowledge Check
If a magnetic material is having magnetic susceptibility (χ)=−1 then the relative magnetic permeability (μr) and type of mangnetic material is
A0, diamagneticB2,ferromagneticC1,paramagneticD−1,diamagneticPoint out the best representation of relation between magnetic susceptibility (Chi) and temperature (T) for a paramagnetic material
A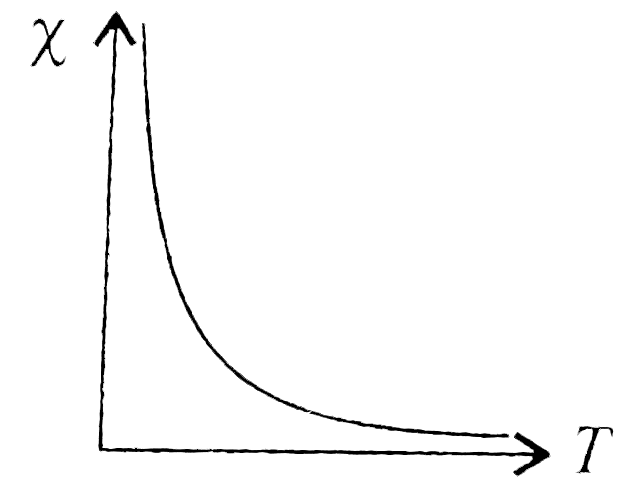 B
B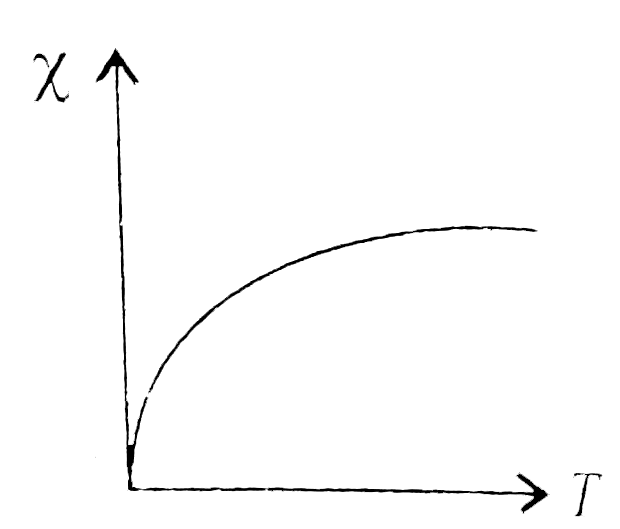 C
C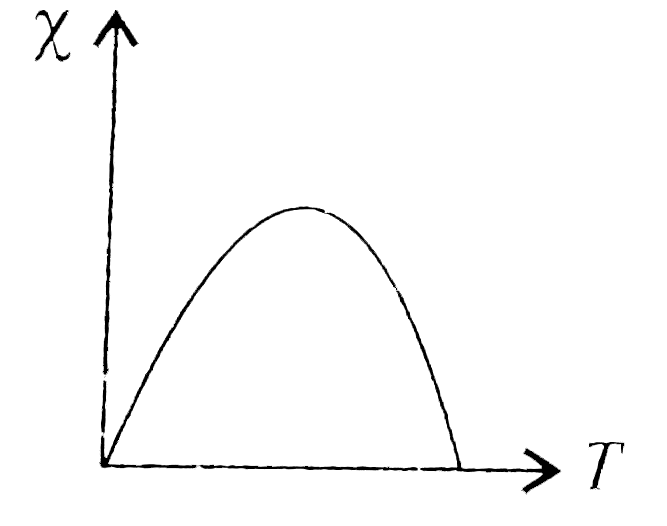 D
D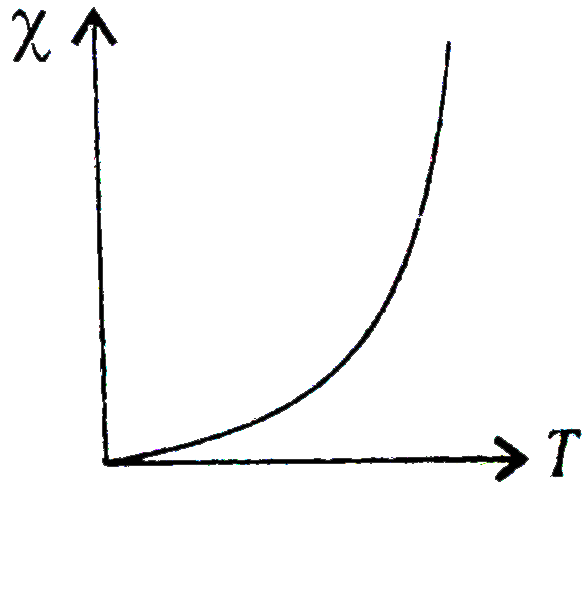
Use real number line to find the range of values of x for which :
x<0and−3≤x<1.
View SolutionFind the number of positive integral values of k for which kx2+(k−3)x+1<0 for atleast one positive x.
View SolutionWhat are the dimensions of χ, the magnetic susceptibility? Consider an H-atom. Guess an expression for χ upto a constant by constructing a quantity of dimensions of χ, out of parameters of the atom: e, m, v, R and μ0. Here, m is the electronic mass, v is electronic velocity, R is Bohr radius. Estimate the number so obtained and compare with the value of ∣∣χ⌈10−5 for any solid material.
View SolutionThe following figure shows the variation of intensity of magnetisation I versus the applied magnetic field intensity H, for two magnetic materials A and B
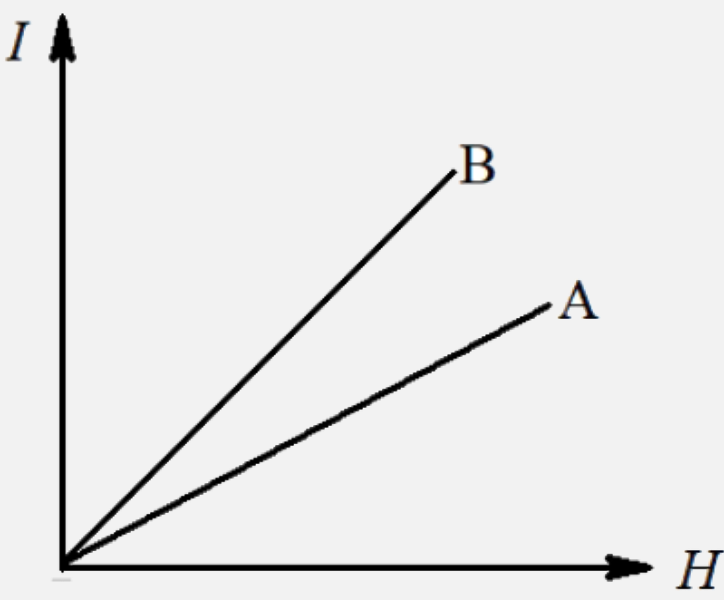
Which of the material have a larger susceptibility for a given field at constant temperature?
View SolutionIf the replacement set is the set of natural numbers, solve :
(i) x−5<0 (ii) x+1≤7
(iii) 3x−4>6 (iv) 4x+1≥17
View SolutionThe magnetic field B and the magnetic intensity H in a material are found to be 1.6Tand1000Am−1 respectively. Calculate the relative permeability μ, and the susceptibiliyt χ of the material.
View Solution
