A slab consists of two parallel layers of iron and brass 10 cm and 10.9 cm thick and of thermal conductivities 500Wm−1K−1and109Wm−1K−1 respectively. The area of opposite faces are 2m2 each and are at temperatures 373 K and 273 K. Find heat conducted per second across the slab and also the temperature of the interface.
The correct Answer is:356.33K,166700Js−1
To solve the problem step by step, we will first find the temperature at the interface between the two layers and then calculate the heat conducted per second across the slab.
Step 1: Identify the given data
- Thickness of iron layer, L1=10cm=0.1m
- Thickness of brass layer, L2=10.9cm=0.109m
- Thermal conductivity of iron, k1=500W/m⋅K
- Thermal conductivity of brass, k2=109W/m⋅K
- Area of the faces, A=2m2
- Temperature at one end (iron side), T1=373K
- Temperature at the other end (brass side), T2=273K
Step 2: Set up the equation for heat conduction
The heat conducted per second through both materials is equal, so we can write:
Qt=k1A(T1−T)L1=k2A(T−T2)L2
Where T is the temperature at the interface.
Step 3: Substitute the known values into the equation
Substituting the values into the equation gives:
500×2×(373−T)0.1=109×2×(T−273)0.109
Step 4: Simplify the equation
This simplifies to:
1000(373−T)=1090(T−273)
Step 5: Expand and rearrange the equation
Expanding both sides gives:
373000−1000T=1090T−297870
Rearranging the equation to isolate T:
373000+297870=1000T+1090T
670870=2090T
Step 6: Solve for T
Now, divide both sides by 2090 to find T:
T=6708702090≈321.33K
Step 7: Calculate the heat conducted per second
Now, we can calculate the heat conducted using the temperature at the interface:
Using the equation for heat conduction through iron:
Qt=k1A(T1−T)L1
Substituting the known values:
Qt=500×2×(373−321.33)0.1
Calculating the difference in temperature:
373−321.33=51.67
Now substituting this back into the equation:
Qt=500×2×51.670.1=500×2×51.670.1=516700W
Final Result
Thus, the heat conducted per second across the slab is approximately 516700J/s.
- Thickness of iron layer, L1=10cm=0.1m
- Thickness of brass layer, L2=10.9cm=0.109m
- Thermal conductivity of iron, k1=500W/m⋅K
- Thermal conductivity of brass, k2=109W/m⋅K
- Area of the faces, A=2m2
- Temperature at one end (iron side), T1=373K
- Temperature at the other end (brass side), T2=273K
The heat conducted per second through both materials is equal, so we can write:
Substituting the values into the equation gives:
This simplifies to:
Expanding both sides gives:
Now, divide both sides by 2090 to find T:
Now, we can calculate the heat conducted using the temperature at the interface:
Thus, the heat conducted per second across the slab is approximately 516700J/s.
Topper's Solved these Questions
- THERMAL CONDUCTIONBook:ICSEChapter:THERMAL CONDUCTIONExercise:SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM THE RATE OF INCREASE OF THICKNESS OF ICE ON A LAKE
Explore 3 Videos
- THERMAL CONDUCTIONBook:ICSEChapter:THERMAL CONDUCTIONExercise:SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM THERMAL RESISTANCE
Explore 7 Videos
- THERMAL CONDUCTIONBook:ICSEChapter:THERMAL CONDUCTIONExercise:SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM RATE OF HEAT FLOW
Explore 6 Videos
- SELF ASSESSMENT PAPER 5Book:ICSEChapter:SELF ASSESSMENT PAPER 5Exercise:Section-D
Explore 6 Videos
- THERMAL RADIATION Book:ICSEChapter:THERMAL RADIATION Exercise:SELECTED PROBLEMS (from WIEN.S DISPLACEMENT LAW)
Explore 14 Videos
Similar Questions
A slab consists of two layers of different materials of the same thickness and having thermal conductivities K1 and K2. The equivalent thermal conductivity of the slab is
View SolutionA slab consists of two parallel layers of copper and brass of the same thichness and having thermal conductivities in the ratio 1:4 If the free face of brass is at 100∘C anf that of copper at 0∘C the temperature of interface is .
View Solution
Knowledge Check
The slab shown in the figure consists of two parallel layers of cooper anb brass of same thickness and having thermal conductivites in the ratio 4:1. IF the free face of the brass is at 100∘C and that of copper is at 0∘C, then the temperature of the interface will be
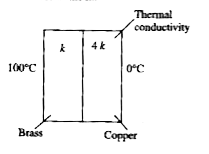 A20∘CB30∘CC40∘CD25∘C
A20∘CB30∘CC40∘CD25∘CConsider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
A23KB√2KC3KD43KA double pan window used for insulating a room thermally from outside consists of two glass sheets each of area 1 m2 and thickness 0.01m separated by 0.05 m thick stagnant air space. In the steady state, the room-glass interface and the glass-outdoor interface are at constant temperatures of 27∘C and 0∘C respectively. The thermal conductivity of glass is 0.8Wm−1K−1 and of air 0.08Wm−1K−1. Answer the following questions.
(a) Calculate the temperature of the inner glass-air interface.
(b) Calculate the temperature of the outer glass-air interface.
(c) Calculate the rate of flow of heat through the window pane.A41.5WB31.5WC21.5WD11.5W
Consider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
View SolutionTwo parallel plates A and B are joined together to form a compound plate . The thicknesses of the plate are 4.0cm and 2.5cm respectively and the area of cross section is 100cm2 for each plate. The thermal conductivities are KA=200Wm−1C−1 for plate A and KB=400Wm−1C−1 for the plate B. The outer surface of the plate A is maintained at100∘C and the outer surface of the plate B is maintained at 0∘C. Find (a) the rate of heat flow through any cross section, (b) the temperature at the interface and (c) the equivalent thermal conductivity of the compound plate.

View SolutionA composite slab is made of two parallel layers of two different materials of thermal conductivities K1andK2 are of same thickness. Show that the equivalent thermal conductivity of the slab is 2K1K2K1+K2
View SolutionFigure shows in cross section a wall consisting of four layers with thermal conductivities K1=0.06W/mK,K3=0.04W/mKandK4=0.10W/mK. The layer thickness are L1=1.5cm,L3=2.8cmandL4=3.5cm. The temperature of interfaces is as shown in figure. energy transfer through the wall is in steady state. the temperature of the interface between layer 3and4 is:

View SolutionFigure shows in cross section a wall consisting of four layers with thermal conductivities K1=0.06W/mK,K3=0.04W/mKandK4=0.10W/mK. The layer thickness are L1=1.5cm,L3=2.8cmandL4=3.5cm. The temperature of interfaces is as shown in figure. energy transfer through the wall is in steady state. the temperature of the interface between layer 3and4 is:

View Solution

