Two plates of equal area are placed in contact with each other. The thickness of the plates are 2.0 cm and 3.0 cm respectively. The outer face of first plate is at −25∘C and that of second plate is at +25∘C. The conductivities of the plates are in the ratio 2:3. Calculate the temperature of the common surface of the plates.
The correct Answer is:0∘C.
To solve the problem, we need to find the temperature of the common surface of two plates in contact, given their thicknesses, outer temperatures, and thermal conductivities. Here’s a step-by-step solution:
Step 1: Understand the Given Information
- Thickness of Plate 1, l1=2cm=0.02m
- Thickness of Plate 2, l2=3cm=0.03m
- Temperature of the outer face of Plate 1, θ1=−25∘C
- Temperature of the outer face of Plate 2, θ2=+25∘C
- Ratio of thermal conductivities, k1:k2=2:3
Step 2: Express the Thermal Conductivities
From the ratio of thermal conductivities, we can express:
k1=23k2
Step 3: Set Up the Heat Transfer Equation
For steady-state heat transfer, the heat flow through both plates must be equal:
k1A(θ1−θ)l1=k2A(θ−θ2)l2
Where A is the area of the plates and θ is the temperature at the common surface.
Step 4: Substitute Known Values
Substituting k1 in terms of k2 into the equation:
23k2A(−25−θ)0.02=k2A(θ−25)0.03
Step 5: Cancel Out Common Terms
Since A and k2 are common on both sides, we can cancel them out:
23(−25−θ)0.02=(θ−25)0.03
Step 6: Simplify the Equation
Cross-multiplying gives:
23(−25−θ)⋅0.03=(θ−25)⋅0.02
This simplifies to:
2⋅0.033(−25−θ)=0.02(θ−25)
Calculating 2⋅0.033=0.02:
0.02(−25−θ)=0.02(θ−25)
Step 7: Eliminate the Common Factor
Dividing both sides by 0.02:
−25−θ=θ−25
Step 8: Solve for θ
Rearranging gives:
−25+25=2θ
0=2θ
Thus,
θ=0∘C
Conclusion
The temperature of the common surface of the plates is 0∘C.
- Thickness of Plate 1, l1=2cm=0.02m
- Thickness of Plate 2, l2=3cm=0.03m
- Temperature of the outer face of Plate 1, θ1=−25∘C
- Temperature of the outer face of Plate 2, θ2=+25∘C
- Ratio of thermal conductivities, k1:k2=2:3
From the ratio of thermal conductivities, we can express:
k1=23k2
For steady-state heat transfer, the heat flow through both plates must be equal:
k1A(θ1−θ)l1=k2A(θ−θ2)l2
Where A is the area of the plates and θ is the temperature at the common surface.
Substituting k1 in terms of k2 into the equation:
23k2A(−25−θ)0.02=k2A(θ−25)0.03
Since A and k2 are common on both sides, we can cancel them out:
23(−25−θ)0.02=(θ−25)0.03
Cross-multiplying gives:
23(−25−θ)⋅0.03=(θ−25)⋅0.02
This simplifies to:
2⋅0.033(−25−θ)=0.02(θ−25)
Calculating 2⋅0.033=0.02:
0.02(−25−θ)=0.02(θ−25)
Dividing both sides by 0.02:
−25−θ=θ−25
Rearranging gives:
−25+25=2θ
0=2θ
Thus,
θ=0∘C
The temperature of the common surface of the plates is 0∘C.
Topper's Solved these Questions
- THERMAL CONDUCTIONBook:ICSEChapter:THERMAL CONDUCTIONExercise:SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM THE RATE OF INCREASE OF THICKNESS OF ICE ON A LAKE
Explore 3 Videos
- THERMAL CONDUCTIONBook:ICSEChapter:THERMAL CONDUCTIONExercise:SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM THERMAL RESISTANCE
Explore 7 Videos
- THERMAL CONDUCTIONBook:ICSEChapter:THERMAL CONDUCTIONExercise:SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM RATE OF HEAT FLOW
Explore 6 Videos
- SELF ASSESSMENT PAPER 5Book:ICSEChapter:SELF ASSESSMENT PAPER 5Exercise:Section-D
Explore 6 Videos
- THERMAL RADIATION Book:ICSEChapter:THERMAL RADIATION Exercise:SELECTED PROBLEMS (from WIEN.S DISPLACEMENT LAW)
Explore 14 Videos
Similar Questions
Two plates of equal areas are placed in contact wih each other. Their thickness are 2.0 cm and 5.0 cm respectively. The temperature of the external surface of the first plate is −20∘C and that of the external surface of the second plate is 20∘C. What will be the temperature of the current surface if the plates (i) are of the same material, (ii) have thermal conductivities in the ratio 2:5.
View SolutionThe length and breadth of a plate are (6±0.1)cmand(4±0.2)cm respectively. The area of the plate is
View SolutionTwo plates of equal area are placed in contact with each other. The thickness of the plates are 2.0 cm and 3.0 cm respectively. The outer face of first plate is at −25∘C and that of second plate is at +25∘C. The conductivities of the plates are in the ratio 2:3. Calculate the temperature of the common surface of the plates.
View SolutionTwo parallel plates A and B are joined together to form a compound plate . The thicknesses of the plate are 4.0cm and 2.5cm respectively and the area of cross section is 100cm2 for each plate. The thermal conductivities are KA=200Wm−1C−1 for plate A and KB=400Wm−1C−1 for the plate B. The outer surface of the plate A is maintained at100∘C and the outer surface of the plate B is maintained at 0∘C. Find (a) the rate of heat flow through any cross section, (b) the temperature at the interface and (c) the equivalent thermal conductivity of the compound plate.

View SolutionA plate has a length (5±0.1) cm and breadth (2±0.01) cm . Then the area of the plate is
View SolutionTwo capacitors of capacitance 2μF and 3μF are joined in series. Outer plate first capacitor is at 1000 volt and outer plate of second capacitor is earthed (grounded). Now the potential on inner plate of each capacitor will be
View SolutionThe plates of a parallel plate capacitance 1.0 F are separated by a distance d =1 cm. Find the plate area .
View SolutionTwo plates, each of area A, are placed parallel to each other at a distance d. One plate is connected to a battery of emf E and its negative is earthed. The other plate is also earthed. The charge drawn by plate is
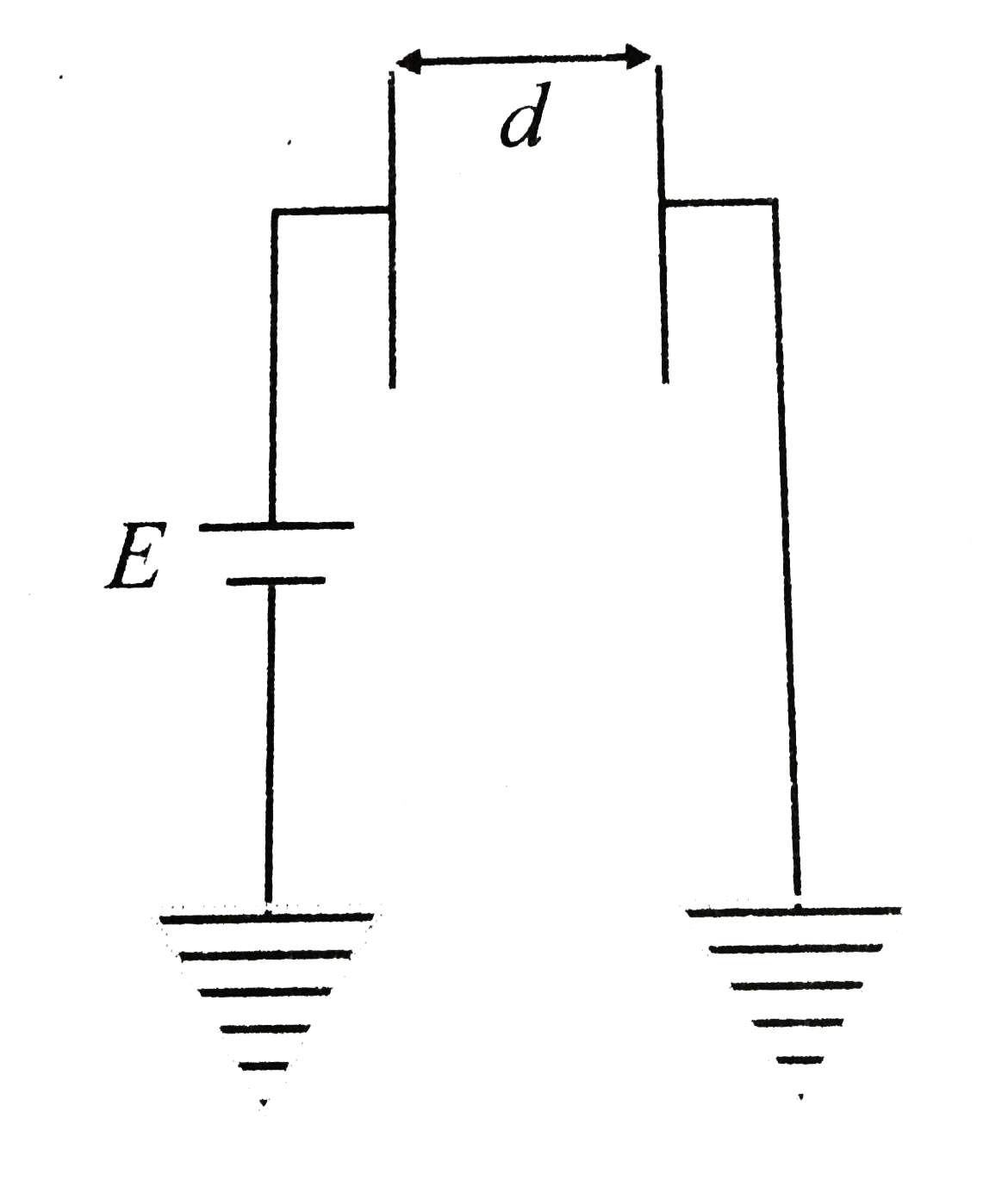
View SolutionThe length and width of a rectangular plate are (16.30±0.05) and (13.80±0.05) cm respectively. Calculate the area of the plate and also find the uncertainty in the area.
View SolutionTwo identical plates of different metals are joined to form a single plate whose thickness is double the thickness of each plate. If the coefficients of conductivity of each plate are 2 and 3 respectively, Then the conductivity of composite plate will be
View Solution