Two rods of same dimensions, but made of different materials are joined end to end to end with their free end being maintained at 100∘C and 0∘C respectively. The temperature of the junction is 70∘C. Then the temperature of the junction if the rods are inerchanged will be equal to T∘C Find T:
The correct Answer is:30
To solve the problem, we will use the concept of thermal resistance and the principle of heat transfer through the two rods.
1. Understanding the Setup:
We have two rods made of different materials, joined end to end. One end of the first rod is maintained at 100∘C and the other end of the second rod is maintained at 0∘C. The temperature at the junction of the two rods is given as 70∘C.
2. Define Thermal Resistances:
Let the thermal resistance of the first rod be R1 and the thermal resistance of the second rod be R2.
3. Heat Transfer Equations:
The rate of heat transfer through the first rod can be expressed as:
Q1=70−0R1=70R1
The rate of heat transfer through the second rod is:
Q2=100−70R2=30R2
4. Equating Heat Transfers:
Since the heat flow through both rods is equal at steady state, we can set Q1=Q2:
70R1=30R2
5. Finding the Ratio of Resistances:
Rearranging the equation gives:
R1R2=7030=73
6. Interchanging the Rods:
Now, when the rods are interchanged, the first rod is now at 0∘C and the second rod is at 100∘C. Let the new temperature at the junction be T∘C.
7. New Heat Transfer Equations:
The heat transfer through the first rod (now at 0∘C) is:
Q′1=T−0R2=TR2
The heat transfer through the second rod (now at 100∘C) is:
Q′2=100−TR1
8. Equating New Heat Transfers:
Again, since the heat flow through both rods is equal, we have:
TR2=100−TR1
9. Substituting the Resistance Ratio:
We know from the previous calculation that R1R2=73, which gives us R1=73R2. Substituting this into the equation:
TR2=100−T73R2
This simplifies to:
3T=7(100−T)1
10. Solving for T:
Expanding and rearranging gives:
3T=700−7T
10T=700
T=70∘C
11. Final Calculation:
Thus, the temperature of the junction when the rods are interchanged is:
T=30∘C
Final Answer:
The temperature T at the junction after interchanging the rods is 30∘C.
We have two rods made of different materials, joined end to end. One end of the first rod is maintained at 100∘C and the other end of the second rod is maintained at 0∘C. The temperature at the junction of the two rods is given as 70∘C.
Let the thermal resistance of the first rod be R1 and the thermal resistance of the second rod be R2.
The rate of heat transfer through the first rod can be expressed as:
Q1=70−0R1=70R1
The rate of heat transfer through the second rod is:
Q2=100−70R2=30R2
Since the heat flow through both rods is equal at steady state, we can set Q1=Q2:
70R1=30R2
Rearranging the equation gives:
R1R2=7030=73
Now, when the rods are interchanged, the first rod is now at 0∘C and the second rod is at 100∘C. Let the new temperature at the junction be T∘C.
The heat transfer through the first rod (now at 0∘C) is:
Q′1=T−0R2=TR2
The heat transfer through the second rod (now at 100∘C) is:
Q′2=100−TR1
Again, since the heat flow through both rods is equal, we have:
TR2=100−TR1
We know from the previous calculation that R1R2=73, which gives us R1=73R2. Substituting this into the equation:
TR2=100−T73R2
This simplifies to:
3T=7(100−T)1
Expanding and rearranging gives:
3T=700−7T
10T=700
T=70∘C
Thus, the temperature of the junction when the rods are interchanged is:
T=30∘C
The temperature T at the junction after interchanging the rods is 30∘C.
Topper's Solved these Questions
- HEAT TRANSFERBook:RESONANCE ENGLISHChapter:HEAT TRANSFERExercise:Exercise-2
Explore 1 Video
- HEAT TRANSFERBook:RESONANCE ENGLISHChapter:HEAT TRANSFERExercise:Exercise-3
Explore 1 Video
- HEAT TRANSFERBook:RESONANCE ENGLISHChapter:HEAT TRANSFERExercise:Exercise-1
Explore 1 Video
- GRAVITATIONBook:RESONANCE ENGLISHChapter:GRAVITATIONExercise:Exercise
Explore 21 Videos
- KINEMATICSBook:RESONANCE ENGLISHChapter:KINEMATICSExercise:Exercise
Explore 65 Videos
Similar Questions
The two rods show in figure have identical geometrical dimension.. They are in contact with two heat baths at temperature 100∘C . And 0∘C . The temperature of the junction is 70∘C . Find the temperature of the junction if the rods are interchanged.

View Solution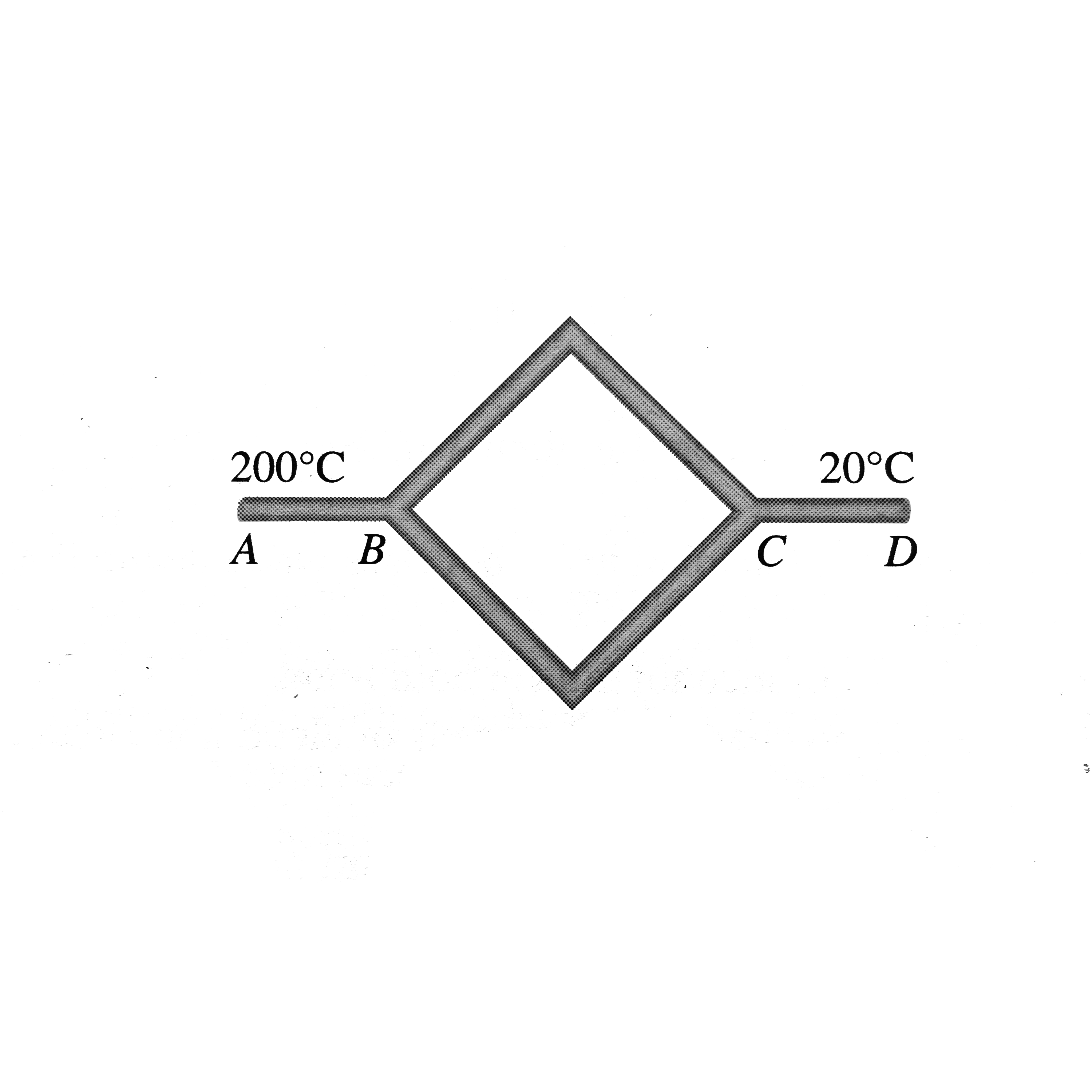
Six identical cunducting rods are joined as shown in Fig. Points A and D are maintained at temperatures 200∘C and 20∘C respectively. The temperature of junction B will be
View Solution
Six identical cunducting rods are joined as shown in Fig. Points A and D are maintained at temperatures 200∘C and 20∘C respectively. The temperature of junction B will be
View Solution
Six identical cunducting rods are joined as shown in Fig. Points A and D are maintained at temperatures 200∘C and 20∘C respectively. The temperature of junction B will be
View SolutionTwo ends of a conducting rod of varying cross-section are maintained at 200∘C and 0∘C respectively. In steady state:

View SolutionTwo rods of similar area of cross section and length are joined as shown in the figure. The ratio of their thermal conductivity is 2:3. The free ends are maintained at 100∘C and 0∘C respectivley. THE temperature at junction in steady state is

View SolutionTwelve conducting rods from the sides of a uniform cube of side l. If in steady state, B and H ends of the cube are at 100∘C and 0∘C respectively. Find the temperature of the junction 'A' :-
_E01_117_Q01.png)
View SolutionThree rods of the same dimensions have thermal conductivities 3k , 2k and k . They are arranged as shown, with their ends at 100∘C,50∘C and 0∘C. The temperature of their junction is :-
_E01_022_Q01.png)
View SolutionThe temperature gradient in a rod of 0.5m length is 80∘C/m. It the temperature of hotter end of the rod is 30∘C, then the temperature of the cooler end is
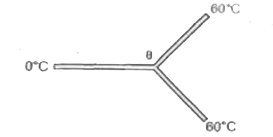
View SolutionThree identical rods have been joined at a junction to make it a Y shape structure .If two free ends are maintained at 60∘C and the thired end is at 0∘C then what is the juction temperature θ?
View Solution