Assume transmitivity t→0 for all the cases:
bad absrober is bad emitter
bad absorber is good reflector
bad reflector is good emitter
bad emitter is good absorbed
The correct Answer is:A, B, C
To solve the question regarding the relationship between emissivity, absorptivity, and reflectivity, we will analyze the given statements based on the principles of heat transfer and thermodynamics.
1. Understanding Emissivity and Absorptivity:
- Emissivity (E) is defined as the ratio of the radiation emitted by a surface to the radiation emitted by a black body at the same temperature. Mathematically, it can be expressed as:
E=QabsorbedQtotal
- Where Qabsorbed is the heat absorbed by the surface and Qtotal is the total incident heat.
2. Heat Absorption Calculation:
- If Q1 is the total heat incident on the surface and Q2 is the heat that is reflected, then the heat absorbed Qabsorbed can be calculated as:
Qabsorbed=Q1−Q2
3. Emissivity in Terms of Incident Heat:
- Substituting the expression for Qabsorbed into the emissivity formula gives:
E=Q1−Q2Q1=1−Q2Q1
4. Analyzing the Statements:
- Statement 1: "Bad absorber is a bad emitter."
- This is true because if a surface does not absorb heat well (bad absorber), it will also not emit heat well (bad emitter). Thus, this statement is correct.
- Statement 2: "Bad absorber is a good reflector."
- This is also true. If a surface does not absorb heat, it must reflect most of it, making it a good reflector. Thus, this statement is correct.
- Statement 3: "Bad reflector is a good emitter."
- This statement is true as well. A bad reflector means that it does not reflect heat effectively, implying that it absorbs heat well, which correlates with being a good emitter. Thus, this statement is correct.
- Statement 4: "Bad emitter is a good absorber."
- This statement is incorrect. A bad emitter indicates that the surface does not emit heat well, which also implies that it does not absorb heat well. Thus, this statement is incorrect.
5. Conclusion:
- From the analysis, we conclude that statements 1, 2, and 3 are correct, while statement 4 is incorrect.
Final Answer:
- Correct Statements: 1, 2, 3
- Incorrect Statement: 4
- Emissivity (E) is defined as the ratio of the radiation emitted by a surface to the radiation emitted by a black body at the same temperature. Mathematically, it can be expressed as:
E=QabsorbedQtotal
- Where Qabsorbed is the heat absorbed by the surface and Qtotal is the total incident heat.
- If Q1 is the total heat incident on the surface and Q2 is the heat that is reflected, then the heat absorbed Qabsorbed can be calculated as:
Qabsorbed=Q1−Q2
- Substituting the expression for Qabsorbed into the emissivity formula gives:
E=Q1−Q2Q1=1−Q2Q1
- Statement 1: "Bad absorber is a bad emitter."
- This is true because if a surface does not absorb heat well (bad absorber), it will also not emit heat well (bad emitter). Thus, this statement is correct.
- Statement 2: "Bad absorber is a good reflector."
- This is also true. If a surface does not absorb heat, it must reflect most of it, making it a good reflector. Thus, this statement is correct.
- Statement 3: "Bad reflector is a good emitter."
- This statement is true as well. A bad reflector means that it does not reflect heat effectively, implying that it absorbs heat well, which correlates with being a good emitter. Thus, this statement is correct.
- Statement 4: "Bad emitter is a good absorber."
- This statement is incorrect. A bad emitter indicates that the surface does not emit heat well, which also implies that it does not absorb heat well. Thus, this statement is incorrect.
- From the analysis, we conclude that statements 1, 2, and 3 are correct, while statement 4 is incorrect.
- Correct Statements: 1, 2, 3
- Incorrect Statement: 4
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - Exercise-21videos
HEAT TRANSFER
- BOOK - RESONANCE ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - Exercise-31videos
HEAT TRANSFER
- BOOK - RESONANCE ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - Exercise-11videos
HEAT TRANSFER
- BOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise21videos
GRAVITATION
- BOOK - RESONANCE ENGLISHCHAPTER - KINEMATICSEXERCISE - Exercise65videos
KINEMATICS
Similar Questions
Van't Hoff factors of aqueous solutions of X,Y,Z are 1.8,0.8and2.5. Hence, their (assume equal concentrations in all three cases)
View Solution(A) : Greater is the height of T.V. transmitting antenna, greater is its range.
(R) : The range of T.V. transmitting antenna is proportional to square root of its height.View SolutionA chain of mass m and length l is kept in three positions as shown below. Assuming (h=0) on the ground find potential energy of chain in all three cases.
(a)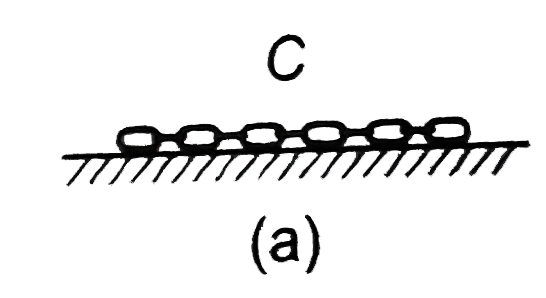
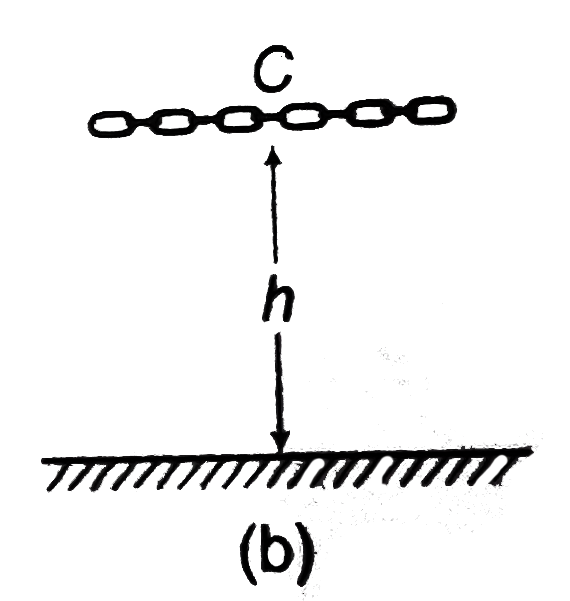
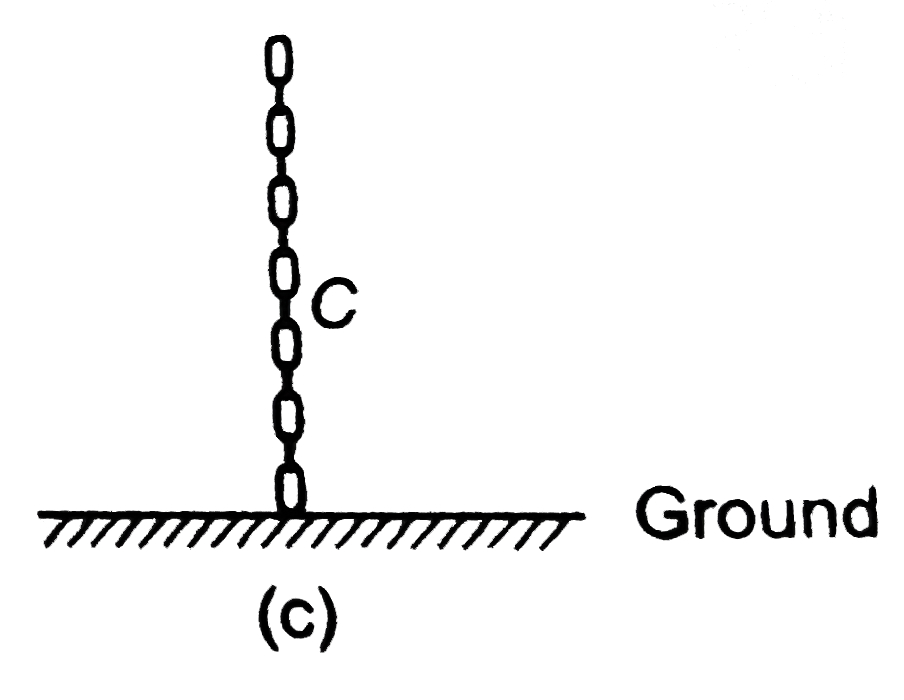 View Solution
View SolutionAssertion : Sexually transmitted diseases get transmitted from the infected to the normal person, only during sexual contact.
Reason : All sexually transmitted diseases can be cured by antibiotics.View SolutionMention whether the following statements are true (T) or false (F).
AIDS is not transmitted by contact with a patient's clothes. T/FView SolutionA coin is tossed thrice and all the eight outcomes are assumed equally likely. In which of the following cases are the following events A and B are independent?
View SolutionAssuming that about 20MeV of energy is released per fusion reaction .1H2+.1H3→.0n1+.2He4, the mass of .1H2 consumed per day in a future fusion reactor of powder 1MW would be approximately
View SolutionThe harmonic wave yi=(2.0×10−3)cosπ(2.0x−50t) travels along a string towards a boundary at x=0 with a second string. The wave speed on the second string is 50m/s. Write expressions for reflected and transmitted waves. Assume SI units.
View SolutionAcceleration of a particle is given by
a=3t2+2t+1
Where t is time . Find
(i) its velocity at time t assuming velocity to be 10 m/s at t = 0.
(ii) its position at time t assuming that the particle is at origin at t = 0.
(iii) What is the average speed of the particle in the duration t = 0 to t = 1s?
(iv) What is the average acceleration of the particle in the duration t = 0 to t = 1s?View SolutionIn YDSE set up (see fig.), the light sources executes SHM between P and Q according to the equation x=Asinωt, S being the mean position. Assume d→0 and A<<L. ω is small enough to neglect Doppler effect. If the sources were stationary at S, intenstiy at O would be I0
Read the paragraph carefully and answer the following questions.
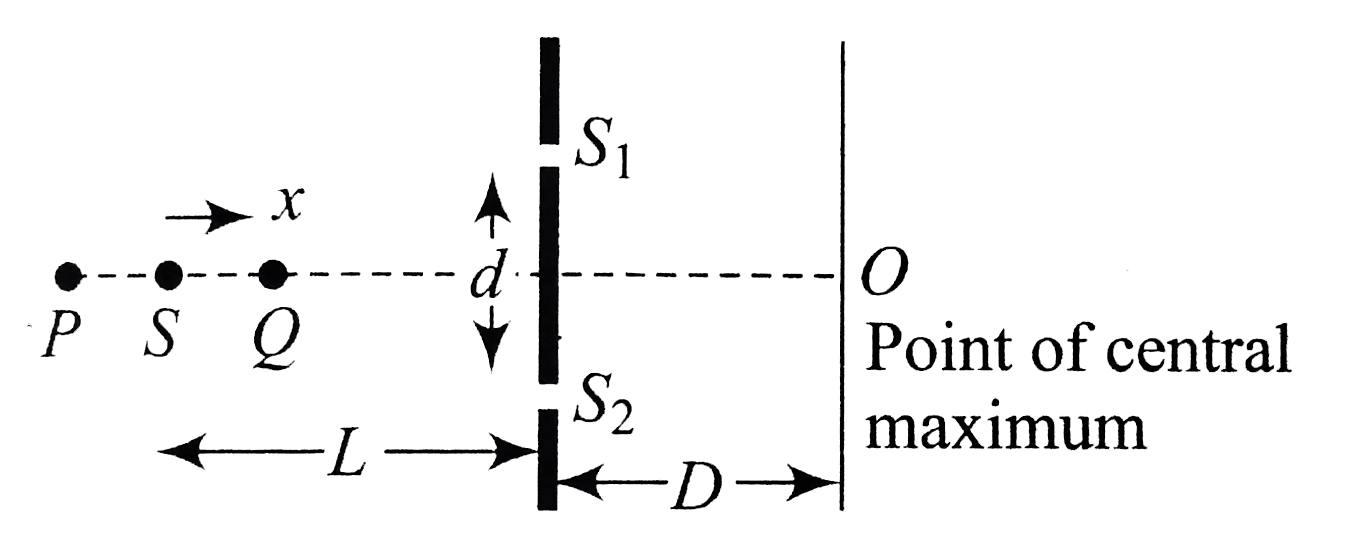
The fractional change in intensity of the central maximum as function of time isView Solution
