A block of mass 50kg is placed as a horizontal table. A spring balance is attached to it and is pulled by gradually increasing the force. When the body just moves, the reading of the spring balance is 50N. Find the coefficient of friction.
The correct Answer is:0.102
To find the coefficient of friction for the block on the horizontal table, we can follow these steps:
1. Identify the Given Values:
- Mass of the block (m) = 50 kg
- Force at which the block starts moving (F) = 50 N
2. Calculate the Weight of the Block:
- The weight (W) of the block can be calculated using the formula:
W=m⋅g
- Where g (acceleration due to gravity) is approximately 9.8m/s2.
- Substituting the values:
W=50kg⋅9.8m/s2=490N
3. Understanding the Forces Involved:
- When the block is just about to move, the force applied (F) is equal to the maximum static friction (f_max).
- The maximum static friction can be expressed as:
fmax=μs⋅N
- Where μs is the coefficient of static friction and N is the normal force. On a horizontal surface, the normal force N is equal to the weight of the block W.
4. Setting Up the Equation:
- Since N=W, we can rewrite the equation for maximum static friction:
fmax=μs⋅W
- Substituting the values we have:
50N=μs⋅490N
5. Solving for the Coefficient of Friction:
- Rearranging the equation to solve for μs:
μs=50N490N≈0.102
6. Final Result:
- Therefore, the coefficient of friction μs is approximately 0.102.
Summary:
The coefficient of friction between the block and the table is approximately 0.102.
- Mass of the block (m) = 50 kg
- Force at which the block starts moving (F) = 50 N
- The weight (W) of the block can be calculated using the formula:
W=m⋅g
- Where g (acceleration due to gravity) is approximately 9.8m/s2.
- Substituting the values:
W=50kg⋅9.8m/s2=490N
- When the block is just about to move, the force applied (F) is equal to the maximum static friction (f_max).
- The maximum static friction can be expressed as:
fmax=μs⋅N
- Where μs is the coefficient of static friction and N is the normal force. On a horizontal surface, the normal force N is equal to the weight of the block W.
- Since N=W, we can rewrite the equation for maximum static friction:
fmax=μs⋅W
- Substituting the values we have:
50N=μs⋅490N
- Rearranging the equation to solve for μs:
μs=50N490N≈0.102
- Therefore, the coefficient of friction μs is approximately 0.102.
The coefficient of friction between the block and the table is approximately 0.102.
Topper's Solved these Questions
Similar Questions
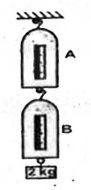
A block of mass 2kg is suspended through two light spring balances A and B. Then A and B will read respectively
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA block of mass 4 kg is suspended through two light spring balances A and B is series. Then A and B will read respectively.
View SolutionA body of mass 50 kg is suspended using a spring balance inside a lift at rest. If the lift startts falling freely, the reading of the spring balance is
View SolutionA block of mass 20kg is placed on a rough horizontal plane and a horizontal force of 12N is applied. If coefficient of friction is 0.1 the frictional force acting on it is,
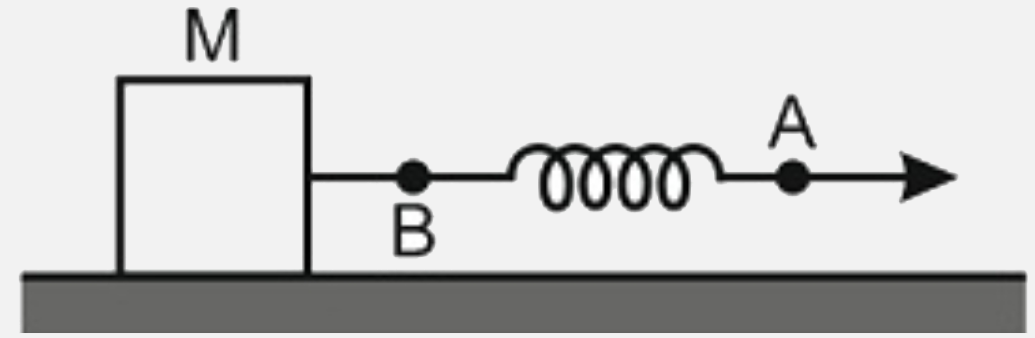
View SolutionA block of mass M is placed on a smooth horizontal surface and it is pulled by a light spring as shown in the diagram. If the ends A and B of the spring are moving with 4ms−2and2ms−1 respectively and the rate at which spring energy is increasing is 20Js−1. then what is the value of spring force (in N)?
View SolutionA block of mass 5kg is placed on a rough horizontal plane whose coefficient of friction is 0.3. Find the least horizontal force needed to move the block along the plane and the resultant of normal reaction and the force applied.
View SolutionA block of mass 5kg rests on a rough horizontal surface. It is found that a force of 10N is required to make the block just move However , once the motion begains, a force of only 8N is enough to maintain the motion find the coefficient of kinetic and static friction between the block and the horizontal surface

View SolutionA block of mass 5kg rests on a rough horizontal surface. It is found that a force of 10N is required to make the block just move However , once the motion begains, a force of only 8N is enough to maintain the motion find the coefficient of kinetic and static friction between the block and the horizontal surface

View SolutionA block of mass m is placed on a smooth horizontal floor is attached to one end of spring. The other end of the spring is attached to fixed support. When spring is vertical it is relaxed. Now the block is pulled to wards right by a force F, which is being increased gradually. When the speing makes angle 53∘ with the vertical, block leaves the floor.

When blocks leaves the table, the normal force on it from table is
View Solution
