A block of mass 4 kg is suspended through two light spring balances A and B is series. Then A and B will read respectively.
4kg and zero kg
4kg and 4kg
zero kg and 4 kg
2kg and 2kg
The correct Answer is:B
To solve the problem of determining the readings of the two spring balances A and B when a block of mass 4 kg is suspended through them in series, we can follow these steps:
1. Identify the Mass and Weight:
- The mass of the block is given as 4 kg.
- The weight (force due to gravity) can be calculated using the formula:
Weight=mass×g
- Here, g (acceleration due to gravity) is approximately 9.8m/s2.
- Therefore, the weight of the block is:
Weight=4kg×9.8m/s2=39.2N
2. Understanding the System:
- The block is suspended, meaning it is in equilibrium. The tension in the spring balances must equal the weight of the block.
- Since the spring balances A and B are in series, the tension in both balances will be the same.
3. Calculate the Tension:
- The tension in the system (which is the same for both spring balances) is equal to the weight of the block:
T=39.2N
4. Convert Tension to Mass Reading:
- The spring balances will read the equivalent mass that corresponds to the tension. To find the mass reading, we can use the formula:
Reading (kg)=Tension (N)g
- Substituting the values:
Reading=39.2N9.8m/s2=4kg
5. Conclusion:
- Therefore, both spring balances A and B will read 4 kg each.
Final Answer:
- The readings of spring balances A and B are both 4 kg.
---
- The mass of the block is given as 4 kg.
- The weight (force due to gravity) can be calculated using the formula:
Weight=mass×g
- Here, g (acceleration due to gravity) is approximately 9.8m/s2.
- Therefore, the weight of the block is:
Weight=4kg×9.8m/s2=39.2N
- The block is suspended, meaning it is in equilibrium. The tension in the spring balances must equal the weight of the block.
- Since the spring balances A and B are in series, the tension in both balances will be the same.
- The tension in the system (which is the same for both spring balances) is equal to the weight of the block:
T=39.2N
- The spring balances will read the equivalent mass that corresponds to the tension. To find the mass reading, we can use the formula:
Reading (kg)=Tension (N)g
- Substituting the values:
Reading=39.2N9.8m/s2=4kg
- Therefore, both spring balances A and B will read 4 kg each.
- The readings of spring balances A and B are both 4 kg.
Topper's Solved these Questions
Similar Questions
A block of mass 2kg is suspended through two light spring balances A and B. Then A and B will read respectively
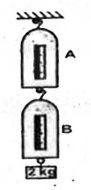
View SolutionA block of mass 10 kg is suspended throug two light spring balances as shown in figure

View SolutionA block of mass 20 kg is suspended through two light spring balances as shown in fig. Calculate the:

(a) reading of spring balance (1),
(b) reading of spring balance (2).
View SolutionA body of mass 8 kg is suspended through two light springs X and Y connected in series as shown in figure. The readings is X and Y respectively are :
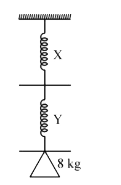
View SolutionA body of mass 8 kg is suspended through two light springs X and Y connected in series as shown in figure. The readings is X and Y respectively are :

View SolutionA block of mass m is suspended by different springs of force constant shown in figure.

View SolutionA block of mass m is suspended through a spring of spring constant k and is in equilibrium. A sharp blow gives the block an initial downward velocity v. How far below the equilibrium position, the block comes to an instantaneous rest?
View SolutionA body of mass 50 kg is suspended using a spring balance inside a lift at rest. If the lift startts falling freely, the reading of the spring balance is
View SolutionA body of mass 5 kg is suspended by a spring balance on an inclined plane as shown in figure. The spring balance measure

View SolutionA block of mass 0.2 kg is suspended from the ceiling by a light string. A second block of mass 0.3 kg is suspended from the first block through another string. Find the tensions in the two strings. Take g=10ms2.
View Solution
