A lift of mass 1000 kg is going up. The variation in the speed of lift is shown in figure. Then the minimum tension in the rope will be (g=10m/s2)
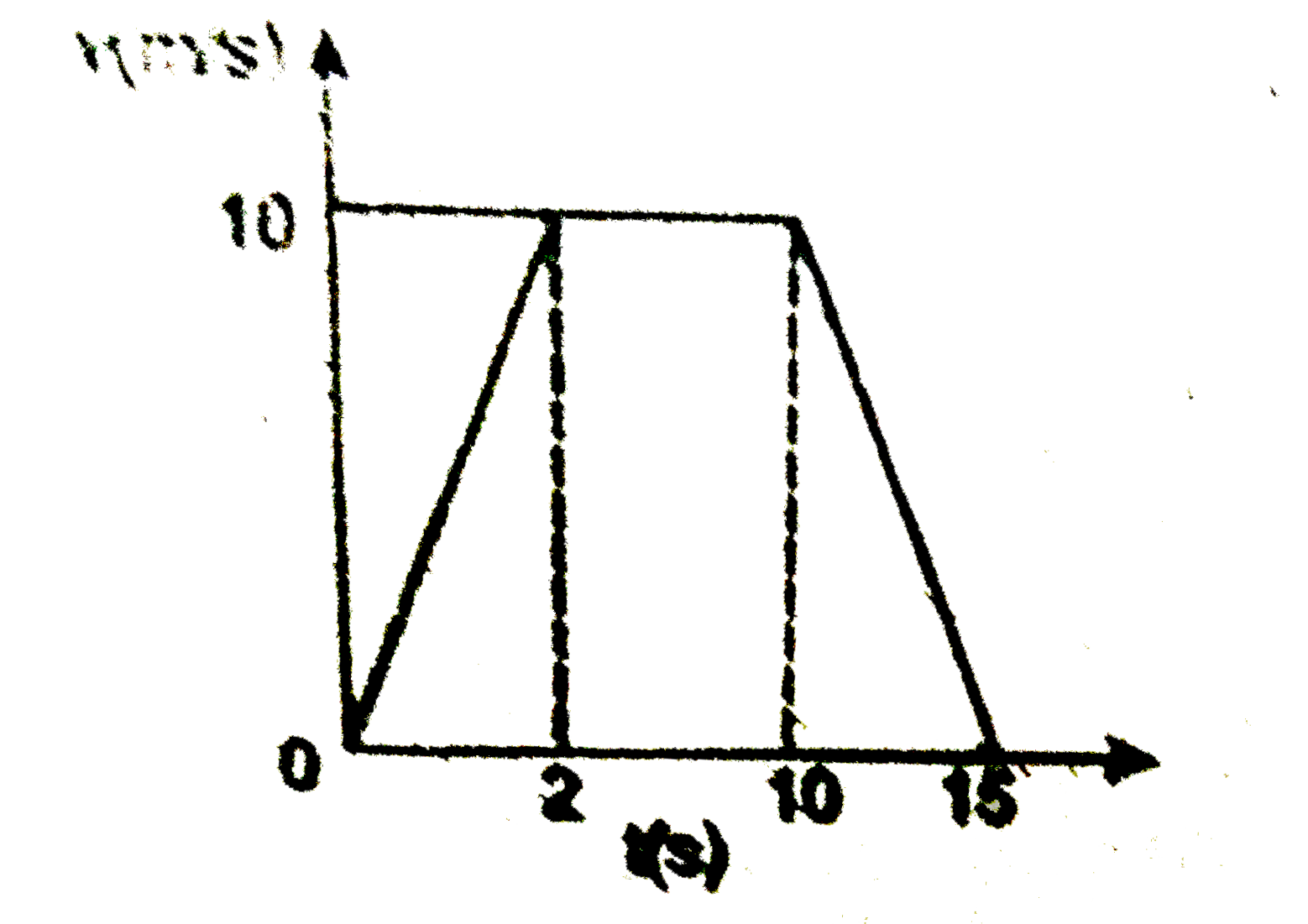
Zero
10000N
12000M
8000 N
The correct Answer is:D
1000g−T=1000×2
T=8000N.
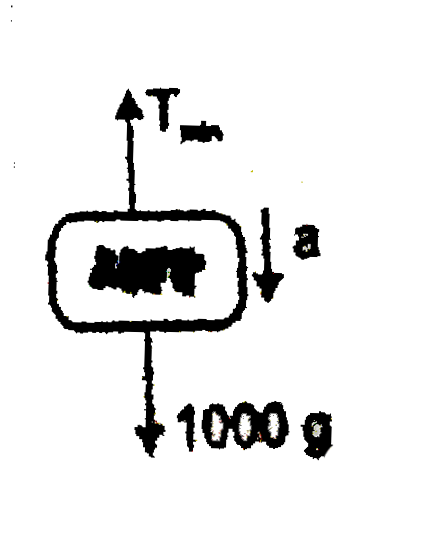
Topper's Solved these Questions
Similar Questions
A lift is going up, the total mass of the lift and the passengers is 1500kg. The variation in the speed of lift is shown in fig. Then the tension in the rope at t = 1 s will be:

View SolutionA lift is going up. The total mass of the lift and the passenger is 1500 kg. The variation in the speed of the lift is as shown in the figure. Find the tension in the rope pulling the lift at t = 11 th second.
View SolutionA lift is going up. The total mass of the lift and the passenger is 1500 kg. The variation in the speed of the lift is as shown in the figure. In the above problem, find the height to which the lift takes the passenger.
View SolutionA lift is going up. The total mass of the lift and the passengers is 1500kg. The variation in the speed of the lift is given by the graph.

(a) What will be the tension in the rope pulling the lift at time t equal to
(i) 1a, (ii) 6s, (iii)11s ?
(b) What will be the average velocity and the average acceleration during the course of the entire motion?
View SolutionThe tension in the cord connected to motor is 15000 N and mass of the lift is 1400 kg. f mass m= 100 kg is inside the connected with a massless string as shown in tigure, then tension in the string connected with m is (g=10ms2)
View SolutionTension in the rope at the rigid support is (g=10m/s2)
View SolutionA lift is going up. The variation in the speed of the lift is as given in the graph in the graph. What is the height to which the lift takes the passengers ?

View SolutionA lift is going up with variable velocity as shown in figure if mass of the lift is 2000 kg Then tension in the rope of lift at t = 5 second is

View SolutionA lift of mass 200 kg is moving upward with an acceleration of 3m/s2 . If g=10m/s2 then the tension of string of the lift will be :
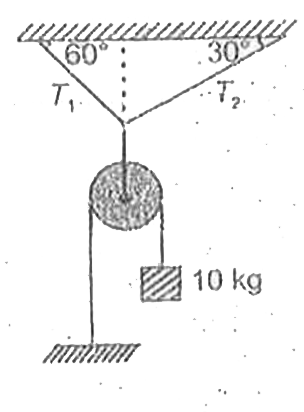
View SolutionIn the arrangement as shown, tension T2 is (g=10m/s2)
View Solution
