A lift is going up. The total mass of the lift and the passenger is 1500 kg. The variation in the speed of the lift is as shown in the figure. In the above problem, find the height to which the lift takes the passenger.
To find the height to which the lift takes the passenger, we can use the concept of the area under the speed-time graph. The area under the graph represents the distance traveled by the lift. In this case, the speed-time graph forms a trapezium.
1. Identify the Parameters:
- The final speed of the lift is 0 m/s (it comes to a stop).
- The initial speed is given as 12 m/s.
- The speed decreases to 8 m/s over a certain time interval.
- The time interval during which the speed changes is 3.6 seconds.
2. Draw the Speed-Time Graph:
- On the x-axis, plot time (0 to 3.6 seconds).
- On the y-axis, plot speed (from 12 m/s to 8 m/s).
- The graph will show a trapezium shape with the top side at 12 m/s, the bottom side at 8 m/s, and the height (time interval) of 3.6 seconds.
3. Calculate the Area of the Trapezium:
- The formula for the area of a trapezium is:
Area=12×(a+b)×h
where a and b are the lengths of the parallel sides, and h is the height (time interval).
- Here, a=12m/s, b=8m/s, and h=3.6s.
4. Substitute the Values:
Area=12×(12+8)×3.6
=12×20×3.6
=10×3.6=36meters
5. Conclusion:
- The height to which the lift takes the passenger is 36 meters.
- The final speed of the lift is 0 m/s (it comes to a stop).
- The initial speed is given as 12 m/s.
- The speed decreases to 8 m/s over a certain time interval.
- The time interval during which the speed changes is 3.6 seconds.
- On the x-axis, plot time (0 to 3.6 seconds).
- On the y-axis, plot speed (from 12 m/s to 8 m/s).
- The graph will show a trapezium shape with the top side at 12 m/s, the bottom side at 8 m/s, and the height (time interval) of 3.6 seconds.
- The formula for the area of a trapezium is:
Area=12×(a+b)×h
where a and b are the lengths of the parallel sides, and h is the height (time interval).
- Here, a=12m/s, b=8m/s, and h=3.6s.
Area=12×(12+8)×3.6
=12×20×3.6
=10×3.6=36meters
- The height to which the lift takes the passenger is 36 meters.
Similar Questions
A lift is going up. The total mass of the lift and the passenger is 1500 kg. The variation in the speed of the lift is as shown in the figure. Find the tension in the rope pulling the lift at t = 11 th second.
View SolutionA lift is going up, the total mass of the lift and the passengers is 1500kg. The variation in the speed of lift is shown in fig. Then the tension in the rope at t = 1 s will be:

View SolutionA lift is going up. The variation in the speed of the lift is as given in the graph in the graph. What is the height to which the lift takes the passengers ?

View SolutionA lift is going up. The total mass of the lift and the passengers is 1500kg. The variation in the speed of the lift is given by the graph.

(a) What will be the tension in the rope pulling the lift at time t equal to
(i) 1a, (ii) 6s, (iii)11s ?
(b) What will be the average velocity and the average acceleration during the course of the entire motion?
View Solution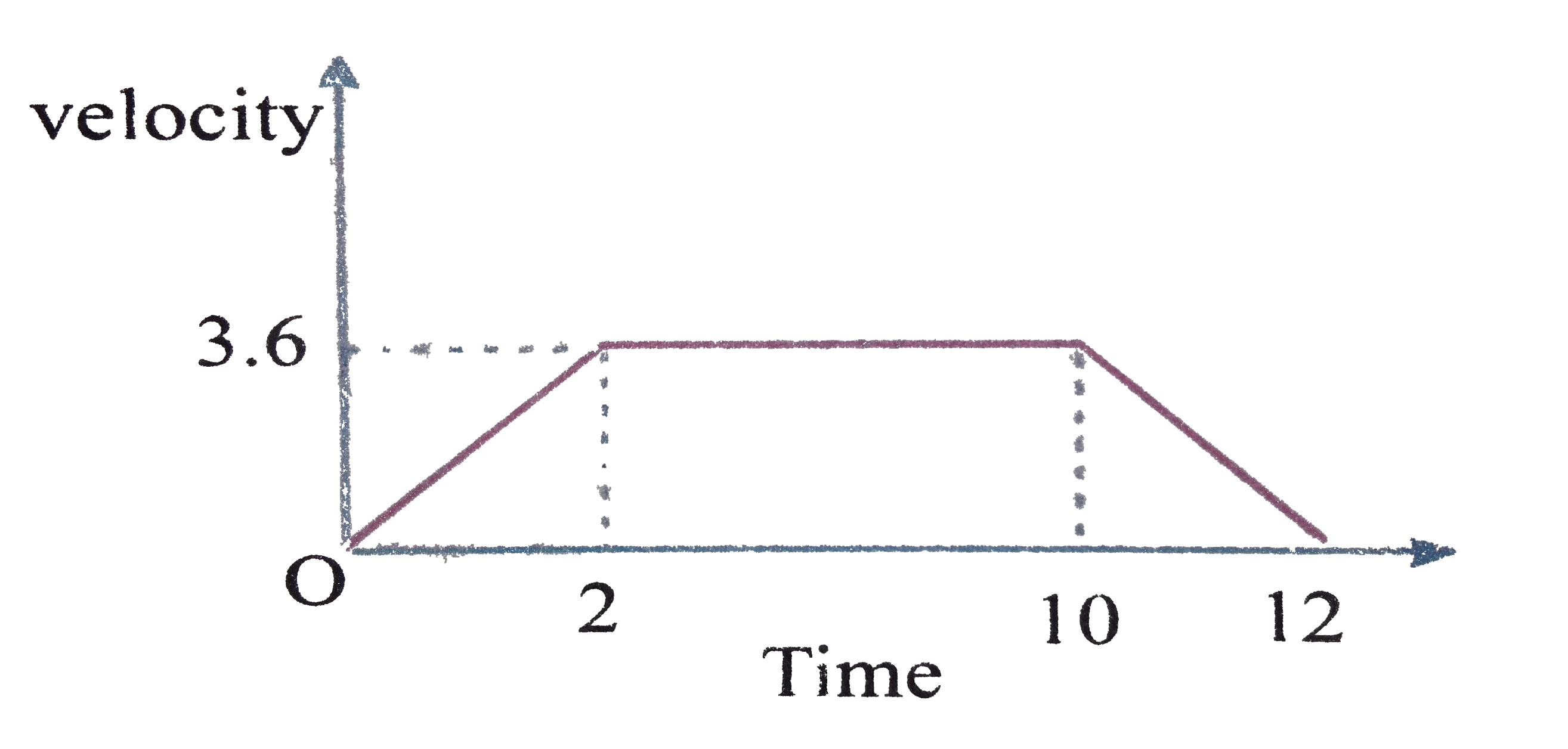
An elevator is going up. The variation in the velocity of the elevator is as given in the graph. What is the height to which the elevator takes the passenger?
View SolutionA lift of mass 1000 kg is going up. The variation in the speed of lift is shown in figure. Then the minimum tension in the rope will be (g=10m/s2)
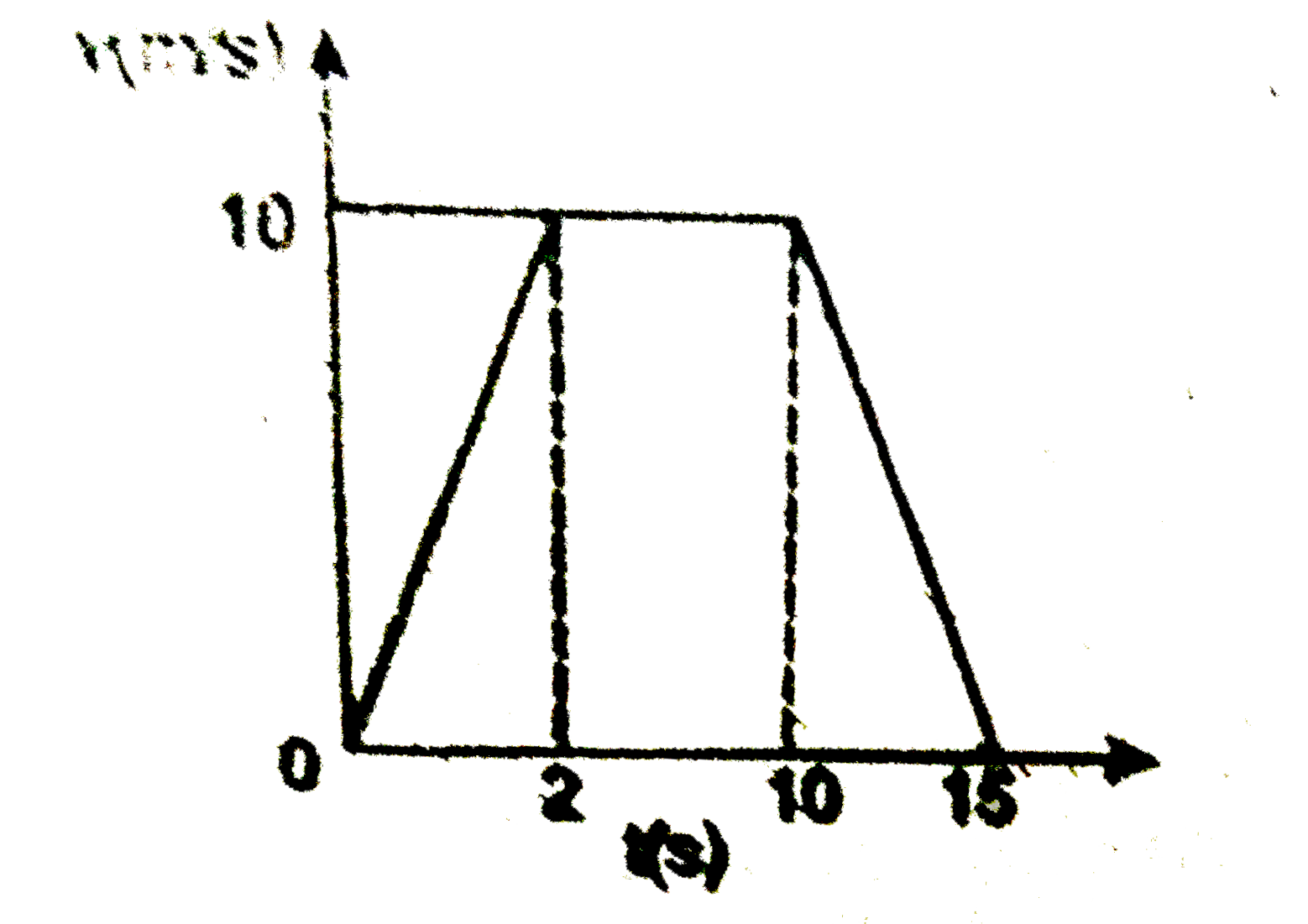
View SolutionA lift is going up with variable velocity as shown in figure if mass of the lift is 2000 kg Then tension in the rope of lift at t = 5 second is

View SolutionThe mass of a lift is 2000kg . When the tensioon in the supporting cable is 28000N , then its acceleration is.
View SolutionBlock A has no relative motion with respect to wedge fixed to the lift as shown in figure during motion-1 or motion-2 Then,

View SolutionA lift is ascending with a constnat speed V. A passenger in the lift drops a coin. The acceleration of the coin towards the floor will be
View Solution

