A block slides on ice with a velocity of 5m/s comes to rest after moving through a distance of 13.5m . Find the coefficient of friction ?
The correct Answer is:0.094
To solve the problem of finding the coefficient of friction for a block sliding on ice, we can use the work-energy theorem. Here’s a step-by-step solution:
Step 1: Understand the Given Information
- Initial velocity of the block, v=5m/s
- Distance traveled before coming to rest, d=13.5m
Step 2: Apply the Work-Energy Theorem
According to the work-energy theorem, the change in kinetic energy of the block is equal to the work done by the friction force.
The initial kinetic energy KEi when the block is moving is given by:
KEi=12mv2
Since the block comes to rest, the final kinetic energy KEf=0.
Step 3: Set Up the Equation
The work done by friction Wf can be expressed as:
Wf=Fr⋅d
where Fr is the friction force.
The friction force can be expressed as:
Fr=μR
where μ is the coefficient of friction and R is the normal force. On a horizontal surface, the normal force R is equal to the weight of the block, mg.
Thus, we can rewrite the work done by friction as:
Wf=μmg⋅d
Step 4: Equate Kinetic Energy to Work Done
From the work-energy theorem, we have:
12mv2=μmg⋅d
We can cancel the mass m from both sides (assuming m≠0):
12v2=μg⋅d
Step 5: Solve for the Coefficient of Friction μ
Rearranging the equation gives:
μ=v22gd
Step 6: Substitute the Known Values
Substituting the values into the equation:
- v=5m/s
- g=10m/s2 (approximate value of acceleration due to gravity)
- d=13.5m
We get:
μ=522⋅10⋅13.5=25270≈0.0926
Final Answer
The coefficient of friction μ is approximately 0.092.
---
- Initial velocity of the block, v=5m/s
- Distance traveled before coming to rest, d=13.5m
According to the work-energy theorem, the change in kinetic energy of the block is equal to the work done by the friction force.
KEi=12mv2
Since the block comes to rest, the final kinetic energy KEf=0.
The work done by friction Wf can be expressed as:
Wf=Fr⋅d
where Fr is the friction force.
Fr=μR
where μ is the coefficient of friction and R is the normal force. On a horizontal surface, the normal force R is equal to the weight of the block, mg.
Wf=μmg⋅d
From the work-energy theorem, we have:
12mv2=μmg⋅d
We can cancel the mass m from both sides (assuming m≠0):
12v2=μg⋅d
Rearranging the equation gives:
μ=v22gd
Substituting the values into the equation:
- v=5m/s
- g=10m/s2 (approximate value of acceleration due to gravity)
- d=13.5m
μ=522⋅10⋅13.5=25270≈0.0926
The coefficient of friction μ is approximately 0.092.
Topper's Solved these Questions
Similar Questions
A ball rolled on ice with a velocity of 14 ms−1 comes to rest after travelling 40 m . Find the coefficient of friction . (Given g=9.8m/s2
View SolutionA ball rolled on ice with a velocity of 14ms−1 comes to rest after travelling 20 m. Find the coefficient of friction. (Given g=9.8m/s2)
View SolutionIn the arrangement shown in figure mA=4.kg and mB=1.0kg. The system is released from rest and block B is found to have a speed 0.3m/s after it has descended through a distance of 1.m find the coefficient of friction between the block and the table. Neglect friction elsewhere. (Take g=10m/s2).
 .
.
View SolutionIn the arrangement shown in figure mA=4.kg and mB=1.0kg. The system is released from rest and block B is found to have a speed 0.3m/s after it has descended through a distance of 1.m find the coefficient of friction between the block and the table. Neglect friction elsewhere. (Take g=10m/s2).
 .
.
View SolutionA body is moving along a rough horizontal surface with an initial velocity 6m/s m If the body comes to rest after travelling 9 m , then the coefficient of sliding friction will be
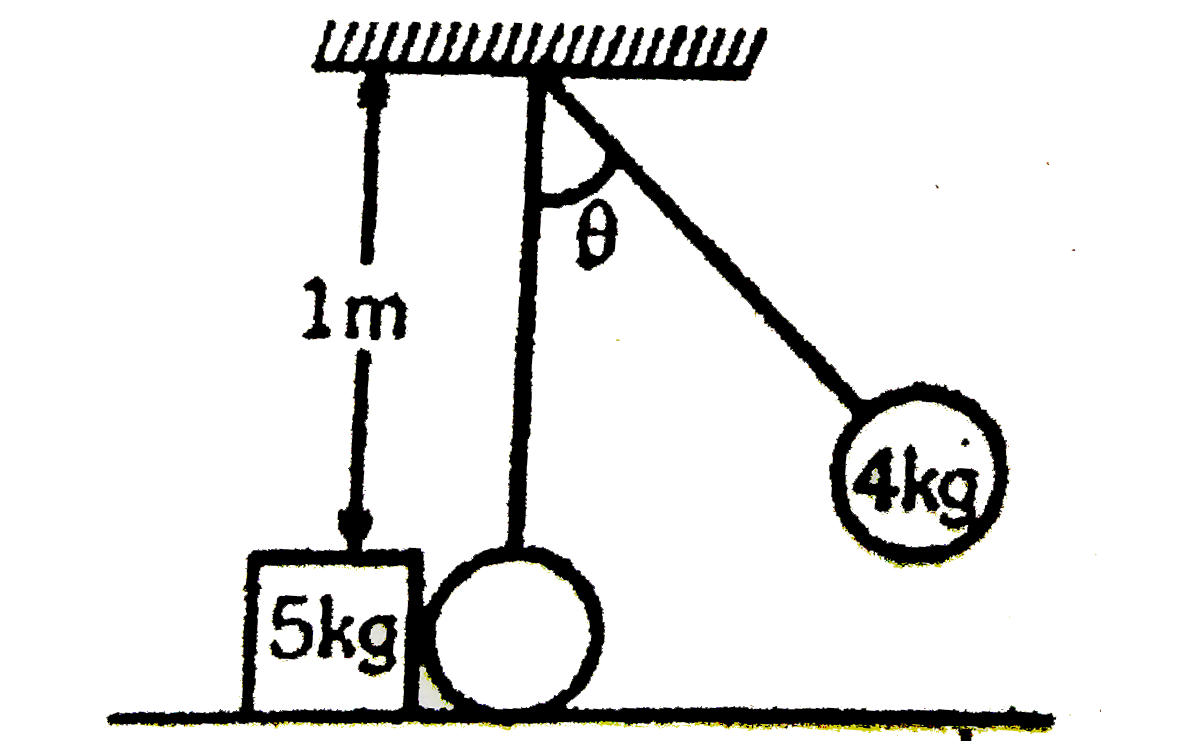
View SolutionThe 4kg sphere form rest when θ=60∘ strikes a block mass of 5kg placed on a rough horizontal plane and comes to rest after collision. The 5kg block comes to rest after moving a distance of 0.8m. Find μ of ground & block & coefficient of restituation e.
View SolutionA marble block of mass 2 kg lying on ice when given a velocity of 6m/s is stopped by friction in 10s. Then the coefficient of friction is
View SolutionA marble block of mass 2 kg lying on ice when given a velocity of 6m/s is stopped by friction in 10s. Then the coefficient of friction is
View SolutionA bullet of mass 0.02 kg travelling horizontally with velocity 250ms−1 strikes a block of wood of mass 0.23 kg which rests on a rough horizontal surface. After the impact, the block and bullet move together and come to rest after travelling a distance of 40m. The coefficient of sliding friction of the rough surface is (g=9.8ms_2)
View SolutionA block of mass m moving at speed υ collides with another block of mass 2 m at rest. The lighter block comes to rest after the collision. Find the coefficient of restitution.
View Solution
