A heavy uniform metal chain is kept on the surface of a horizontal table. The coefficient of friction between the chain and the table surface is . Find the maximum fraction of length of the chain that could hung over on one edge of the table ?
To solve the problem of finding the maximum fraction of the length of the chain that could hang over the edge of the table, we can follow these steps:
Step 1: Understand the Problem
We have a heavy uniform metal chain on a horizontal table. The coefficient of friction between the chain and the table is given as μ=0.22. We need to find the maximum length of the chain that can hang over the edge of the table without slipping.
Step 2: Define Variables
Let:
- L = Total length of the chain
- l = Length of the chain hanging over the edge
- m = Mass per unit length of the chain
- g = Acceleration due to gravity (approximately 9.81m/s2)
Step 3: Calculate Forces
The weight of the hanging portion of the chain is given by:
W=m⋅l⋅g
The frictional force that can act on the chain to prevent it from slipping is given by:
Ffriction=μ⋅N
where N is the normal force acting on the chain on the table. The normal force is equal to the weight of the portion of the chain that is on the table, which is:
N=m⋅(L−l)⋅g
Thus, the frictional force can be expressed as:
Ffriction=μ⋅m⋅(L−l)⋅g
Step 4: Set Up the Equation
For the chain to remain in equilibrium, the weight of the hanging portion must be equal to the maximum frictional force:
m⋅l⋅g=μ⋅m⋅(L−l)⋅g
We can cancel m and g from both sides (assuming m and g are not zero):
l=μ⋅(L−l)
Step 5: Solve for l
Rearranging the equation gives:
l+μ⋅l=μ⋅L
l(1+μ)=μ⋅L
l=μ⋅L1+μ
Step 6: Calculate the Maximum Fraction
The maximum fraction of the length of the chain that can hang over the edge is given by:
Fraction=lL=μ1+μ
Substituting μ=0.22:
Fraction=0.221+0.22=0.221.22≈0.1803
Step 7: Final Answer
Thus, the maximum fraction of the length of the chain that could hang over the edge of the table is approximately 0.1803 or 18.03%.
---
We have a heavy uniform metal chain on a horizontal table. The coefficient of friction between the chain and the table is given as μ=0.22. We need to find the maximum length of the chain that can hang over the edge of the table without slipping.
Let:
- L = Total length of the chain
- l = Length of the chain hanging over the edge
- m = Mass per unit length of the chain
- g = Acceleration due to gravity (approximately 9.81m/s2)
The weight of the hanging portion of the chain is given by:
W=m⋅l⋅g
The frictional force that can act on the chain to prevent it from slipping is given by:
Ffriction=μ⋅N
where N is the normal force acting on the chain on the table. The normal force is equal to the weight of the portion of the chain that is on the table, which is:
N=m⋅(L−l)⋅g
Thus, the frictional force can be expressed as:
Ffriction=μ⋅m⋅(L−l)⋅g
For the chain to remain in equilibrium, the weight of the hanging portion must be equal to the maximum frictional force:
m⋅l⋅g=μ⋅m⋅(L−l)⋅g
We can cancel m and g from both sides (assuming m and g are not zero):
l=μ⋅(L−l)
Rearranging the equation gives:
l+μ⋅l=μ⋅L
l(1+μ)=μ⋅L
l=μ⋅L1+μ
The maximum fraction of the length of the chain that can hang over the edge is given by:
Fraction=lL=μ1+μ
Substituting μ=0.22:
Fraction=0.221+0.22=0.221.22≈0.1803
Thus, the maximum fraction of the length of the chain that could hang over the edge of the table is approximately 0.1803 or 18.03%.
Topper's Solved these Questions
- FRICTIONBook:ICSEChapter:FRICTIONExercise:Conceptual short answer questions with answer
Explore 9 Videos
- FRICTIONBook:ICSEChapter:FRICTIONExercise:Long answer questions
Explore 2 Videos
- FRICTIONBook:ICSEChapter:FRICTIONExercise:Selected problems
Explore 30 Videos
- DYNAMICSBook:ICSEChapter:DYNAMICSExercise:SHORT ANSWER QUESTIONS WITH ANSWERS
Explore 12 Videos
- GRAVITATIONBook:ICSEChapter:GRAVITATIONExercise:FROM THE HUBBLE TELESCOP
Explore 2 Videos
Similar Questions
A heavy uniform chain lies on horizontal table top. If the co-efficient of friction between the chain and the table surface is 0.5, the maximum percentage of the length of the chain that can hang over one edge of the table is
View SolutionA heavy uniform chain lies on horizontal table top. If the coefficient of friction 0.25, then the maximum fraction of length of the chain that can hang over on one edge of the table is
View Solution
Knowledge Check
A heavy uniform chain lies on horizontal table top. If the coefficient of friction between the chain and the table surface is 0.25, then the maximum fraction of the length of the chain that can hang over one edge of the table is
A0.2B0.25C0.35D0.15A 20 N block is being pushed across a horizontal table by an 18 N force. If the coefficient of kinetic friction between the block and the table is 0.4, find the acceleration of the block.
A0.5m/s2B1m/s2C5m/s2D7.5m/s2
A homogoneous chain of length L lies on a table. The coefficient of friction between the chain and the table is μ. The maximum length which can hang over the table in equilibrium is
View SolutionA block is kept on a horizontal table. The table is undergoing simple farmonic motion of frequency 3Hz in a horizontal plane. The coefficient of static friction between the block and the table surface is 0.72. find the maximum amplitude of the table at which the block does not slip on the surface g=10ms−1
View SolutionA uniform chain of mass m and length I is kept on the table with a part of it overhanging (see figure). If the coefficient of friction between the table and the chain is 1/3 then find the maximum length of the chain that can overhang such that the chain remain in equilibrium.
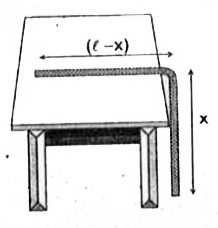
View SolutionA homogeneous chain lies in limiting equilibrium on a horizontal table of coefficient of friction 0.5 with part of it hanging over the edge of the table. The fractional length of the chain hanging down the edge of the table is
View SolutionA block is kept on a horizontal table. The stable is undergoing simple harmonic motion of frequency 3Hz in a horizontal plane. The coefficient of static friciton between block and the table surface is 0.72. find the maximum amplitude of the table at which the block does not slip on the surface.
View SolutionA chain is placed on a rough table, partially hanging, as shown in the figure. The coefficient of static friction between the chain and the table is μ = 0.4. If the maximum possible length of the hanging part is x and the length of the chain is L, then what is the value of Lx?
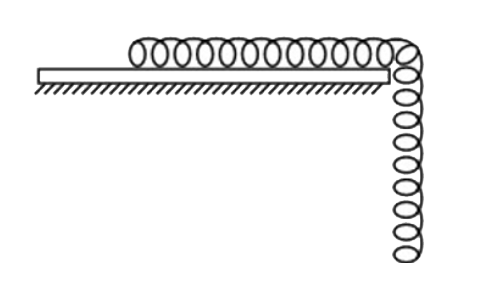
View Solution

