A block of mass 5kg is put on the top of a 6kg block placed on a frictionless table. A horizontal force of 15N must be applied to stop the top block to cause it to slip on the bottom block as shown in Fig.. Find the maximum horizontal force F that must be applied to the lower block so that the blocks will move together and the resulting acceleration of the blocks.

The force of friction between the top and bottom block is
fs=μsm1g
μs=fsm1g=155×9.8=0.306
Let the acceleration of the system be a. When a≤μsg the top block will not slip. The corresponding acceleration a=μsg=0.306×9.8=3ms−2.
Maximum force that can be applied on the bottom block =F=(m1+m2)a
=(5+6)×3=33N
Topper's Solved these Questions
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Conceptual short answer questions with answer
9 Videos
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Long answer questions
2 Videos
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Selected problems
30 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS
12 Videos
- GRAVITATIONBOOK - ICSECHAPTER - GRAVITATIONEXERCISE - FROM THE HUBBLE TELESCOP
2 Videos
Similar Questions
A 4.0 kg block is put on top of a 5.0kg block. In order to cause the top block to slip on the bottom one, a horizontal force of 12N must be applied to the top block. Assuming a friction less table the maximum horizontal force F which can be applied to the lower block so that the blocks, will move together should be

View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View Solution
Knowledge Check
The coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?
 A0.15mgB0.05mgC0.1mgD0.45mg
A0.15mgB0.05mgC0.1mgD0.45mgA block A of mass 4 kg is placed on another block B of mass 5 kg and the block rests on a smooth horizontal table. For sliding the block A on B, a horizontal force of 12 N is required to be applied on it. The maximum horizontal force that can be applied on B so that both A and B move together and the acceleration produced by this force is
 A25 N, 5 m/s2B27 N, 3 m/s2C30 N, 8 m/s2Dcannot be calculated from the given data.
A25 N, 5 m/s2B27 N, 3 m/s2C30 N, 8 m/s2Dcannot be calculated from the given data.
Blocks are in contact on a frictionless table. A horizontal force F=3N is applied to one block as shown. The force exerted by the smaller block m2 on block m1 is :
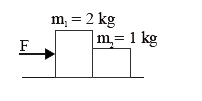
View SolutionFor the two blocks shown in the adjacent figure, an external force of 18N is applied on the lower block. Find the acceleratiion of the upper block.
View SolutionA block of mass m is placed on another block of mass M lying on a smooth horizontal surface as shown in the figure. The co-efficient of friction between the blocks is μ. Find the maximum horizontal force F (in Newton) that can be applied to the block M so that the blocks together with same acceleration? (M=3kg,m=2kg,μ=0.1,g=10m/s2)

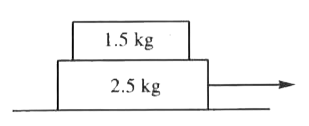
View SolutionOn a smooth table two blocks of masses 2.5kg and 1.5kg are placed one over the other as shown in figure. If the coefficient of static friction between two blocks is 0.2, the maximum horizontal force to be applied on the lower block so that the two blocks move together is (g = ms−2)
View SolutionTwo blocks of masses 2 kg and 1 kg are in contact with each other on a frictionless table. When a horizontal force of 3.0 N is applied to the block of mass 2 kg the value of the force of contact between the two blocks is:
View SolutionTwo blocks of masses 2 kg and 1 kg are in contact with each other on a frictionless table. When a horizontal force of 3.0 N is applied to the block of mass 2 kg the value of the force of contact between the two blocks is:
View Solution
