A small object loops a vertical loop in which a symmetrical section of angle 2α has been removed (Fig.) Find the maximum and the minimum heights from which the object, after loosing contact with the loop at point A and flying through the air, will reach point B. Find the corresponding angles of the section removed for which this is possible.
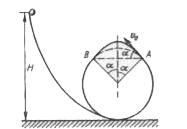
The correct Answer is:(1+√2)R≤H≤2.5R;45∘,60∘
The object thrown at an initial speed v0 at an angle α to the horizontal must fly through the air a distance AB = L = 2R sin α. We know (see ) that
L=2v20sinαcosαg
So v20=gRcosα
To find the speed v0 apply the law of conservation of energy
mgH=mgH(1+cosα)+12mv20
for which k=HR=1+cosα+12cosα.
For the computation of cosα
we obtain an equation
2cos2α−2(k−1)cosα+1=0
cosα=12(k−1±√(k−1)2−2)
Since the number under the root sign must be non - negative , we obtain k−1≥√2 i.e. k≥1+√2.
On the other hand 0<cosα≤1, i.e. k−1+√(k−1)2−2≤≤2andk≤2.5. Thus
1+√2≤k≤2.5, i.e. (1+√2)R≤H≤2.5R
For the limiting values of the cosines we have
cosα=√22,e.α1=45∘
cosα=(1.5±0.5)/2,cosα2=0.5,cosα3=1
Obviously the solution cosα3=1 does not satisfy the condition of the problem since for α3=0 there will be no cut. So the remaining solution is cosα2=0.5,α2=60∘
Accordingly for the heights in the range (1+√2)R≤H≤≤2.5R corresponding suitable cuts are those with angles of 45∘≤≤α≤60∘ chosen so as to satisfy the condition
cosα=12(k−1−√k2−2k−1)
Similar Questions
A small object slides without friction from the height 5R/2 and then loops of the verticle loop of radius R from which a symmetrical section of angle 2α has been removed. Find angle α such that after losing contact at A and flying through the air, the object will reach point B.
 View Solution
View SolutionFind the centre of mass of a uniform disc of radius a from which a circualr section of radius b has been removed. The centre of hole is at a distance c from the centre of the disc.
View SolutionFind the centre of mass of a unifrom disc of radius a from which a circulr section of radius b has been removed. The centre of hole is at a distance c from the centre of the disc.
View SolutionA ball is thrown with the velocity u at an angle of α to the horizon. Find (i) the height of which the ball will rise to (ii) the distance x from the point of projection to the point where it reaches to the ground and (iii) the time during which the ball will be in motion (neglect the air resistance ).
View SolutionA conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.

(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.View SolutionA conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.

(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.View SolutionFigure shows a an incline which ends into a circular track of radius R. What should be the minimum value of height (h), so that the small object shown after release, is able to complete the loop. Neglect friction.
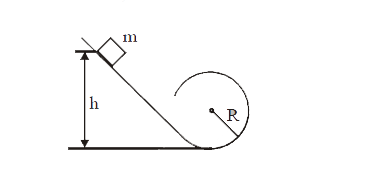 View Solution
View SolutionA parachutist is descending vertically and makes angles of elevation of 45∘ and 60∘ at two observing points 100m apart from each other on the left side of himself. Find the maximum height from which he falls and the distance of the point where he falls on the ground from the just observation point.
View SolutionA parachutist is descending vertically and makes angles of elevation of 45o and 60o at two observing points 100m apart from each other on the left side of himself. Find the maximum height from which he falls and the distance of the point where he falls on the ground from the just observation point.
View SolutionA tower stands vertically on the ground. From a point on the ground, which is 15m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 60∘ . Find the height of the tower.
View Solution

