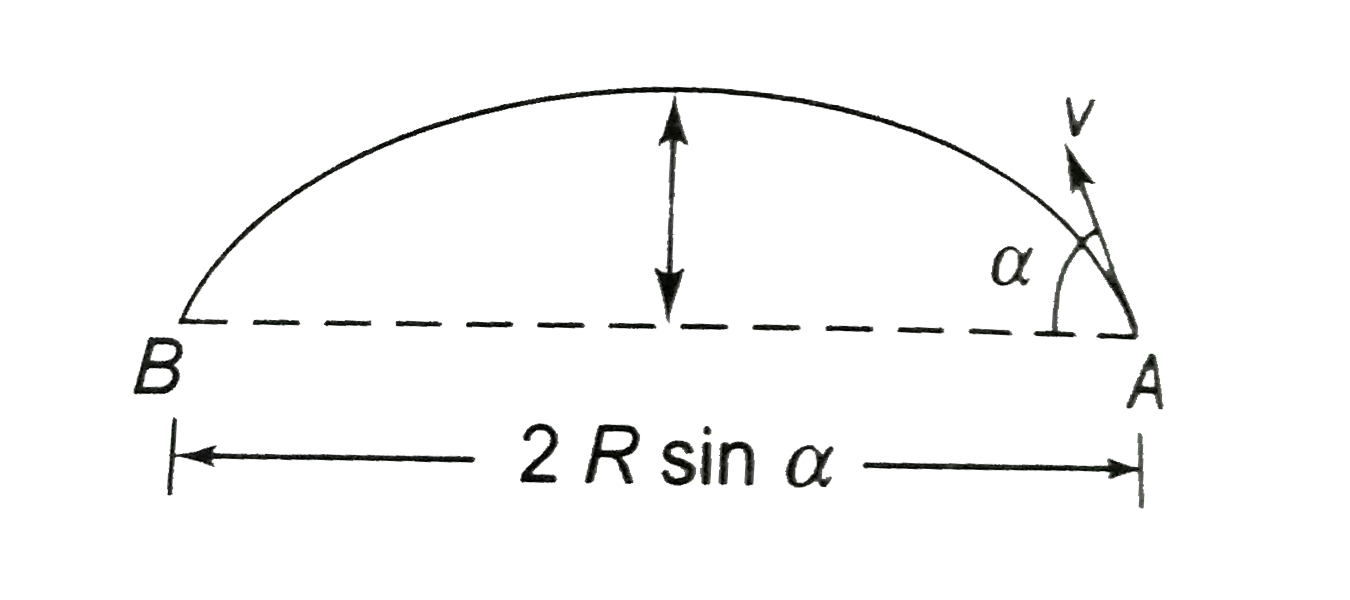
A small object slides without friction from the height 5R/2 and then loops of the verticle loop of radius R from which a symmetrical section of angle 2α has been removed. Find angle α such that after losing contact at A and flying through the air, the object will reach point B.

When the block reaches at P, its velocity
u=√2gh=√2g×5R2=√5gR
Velocity at the lowest point ≥√5gR, hence the block will complete vertical circle. But at A, there is cut, hence it will leave vertical circle due to the cut at A.
Let the velocity at A be v.
V2=u2+2gh=0+2g[5R2−R(1+cosα)]
=2g(3R2−Rcosα)
A toB (projectile motion)
Range=v2sin2αg
2Rsinα=2g[3R2−Rcosα]sin2αg
sinα=(32−cosα)(2sinαcosα)
1=(3−2cosα)(cosα)
2cos2α−3cosα+1=0
cosα=3±√9−84=3±14
cosα=1⇒α=0∘, not possible
cosα=12⇒α=60∘
Topper's Solved these Questions
Similar Questions
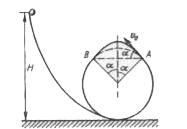
A small object loops a vertical loop in which a symmetrical section of angle 2α has been removed (Fig.) Find the maximum and the minimum heights from which the object, after loosing contact with the loop at point A and flying through the air, will reach point B. Find the corresponding angles of the section removed for which this is possible.
View SolutionA body slides without friction from a height H=60cm and then loops the loop of radius R=20cm at the bottom of an incline. Find the ratio of forces exerted on the body by the track at the positions A,B and C(g=10ms−2).
 .
.
View Solution
Knowledge Check
A small object of mass m starts from rest at the position shown and slides along the fricationless loop-the -loop track of radius R. What is the smallest value of y such that the object will slide without losing contact with the track?
 AR/4BR/2CRD2R
AR/4BR/2CRD2RA small of mass m starts from rest at the position shown and slides along the frictionless loop the loop track of radius R. What is the smallest value of y such that the object will slide without losing contact with the track?
 AR/2BRCR/4D3R/4
AR/2BRCR/4D3R/4A body slides without friction from a height H=60cm and then loops the loop of radius R=20cm at the bottom of an incline. Find the ratio of forces exerted on the body by the track at the positions A,B and C(g=10ms−2).
 .A7:3:1B5:3:1C7:4:1D1:4:7
.A7:3:1B5:3:1C7:4:1D1:4:7
The block on the loop shown slides without friction. At what height from A it starts so that it passes against the track at B with a net upward force equal to its own weight? The radius of the loop is R.
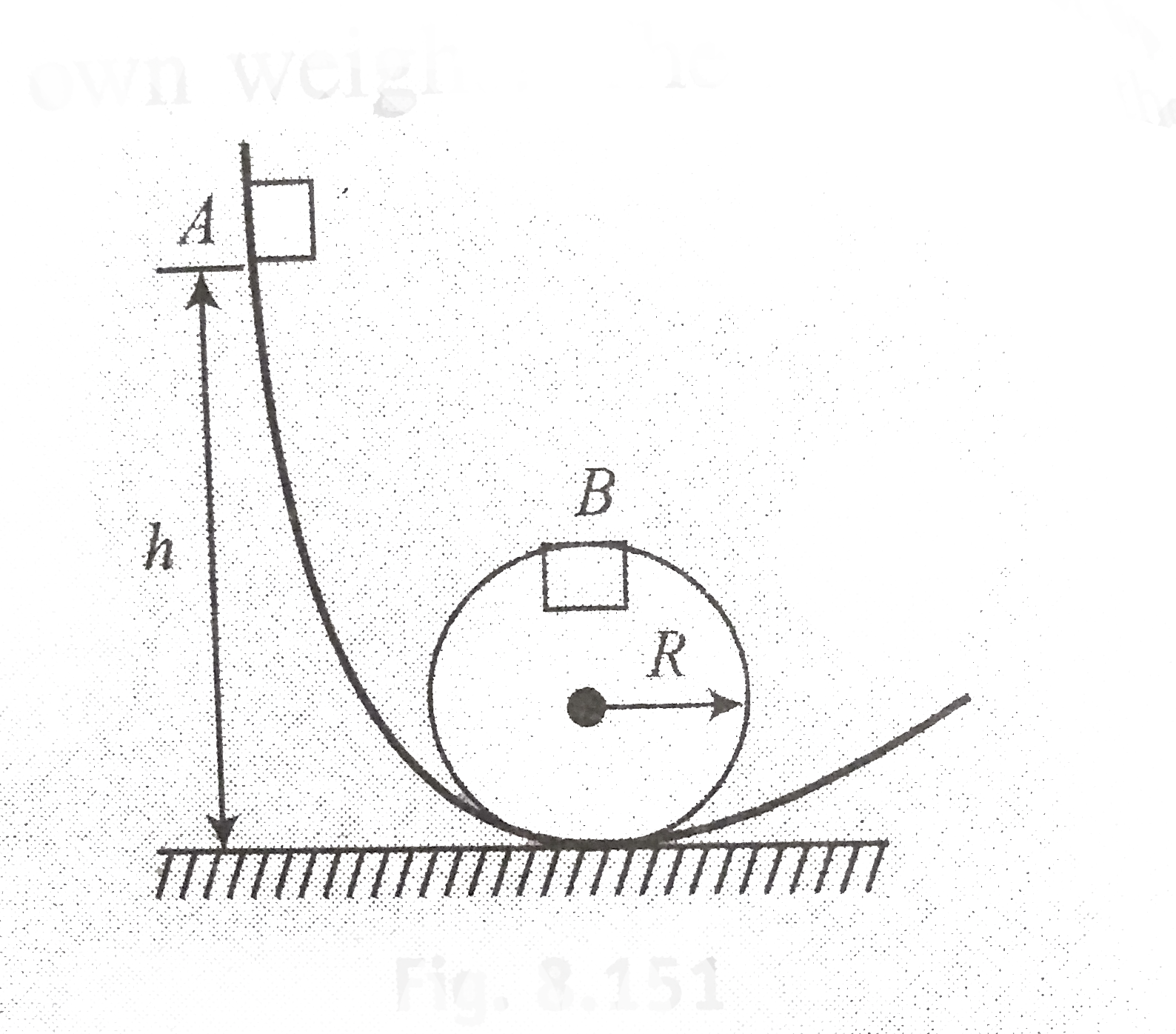
View SolutionA circular loop has a small bead which can slide on it without friction. The radius of the loop is r. Keeping the loop vertically it is rotated about a vertical diameter at a constant angular speed ω. What is the value of angle θ, when the bead is in dynamic equilibrium ?
View SolutionThe angle of elevation of the top of the tower observed from each of three points A,B , C on the ground, forming a triangle is the same angle α. If R is the circum-radius of the triangle ABC, then find the height of the tower
View SolutionA balloon of radius r subtends an angleα at the eyes of an observer and the center of balloon from the eye is β . Find the height of the center of the balloon from the eye of observer .
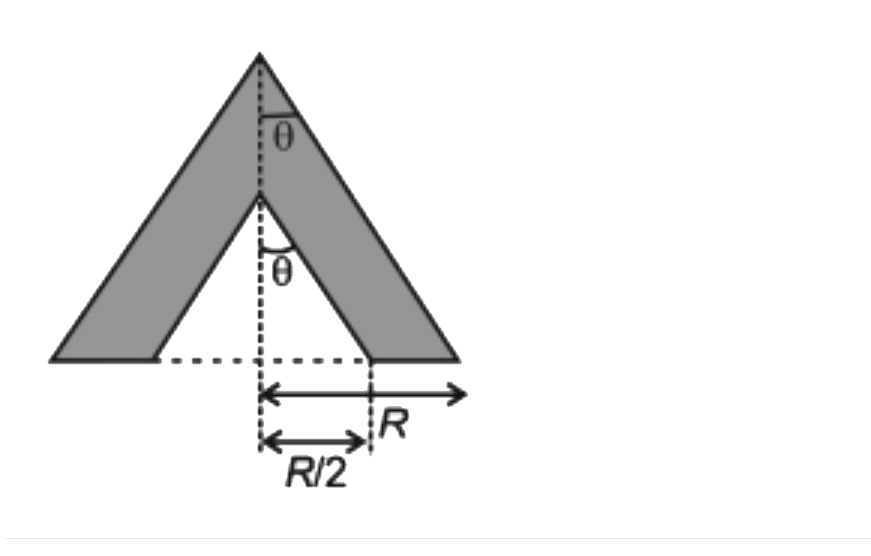
View SolutionFrom a uniform solid cone of base radius R and height H, a symmetric cone of the base radius R2 is removed as shown. Then the centre of mass is shifted by H/n. Find the value of of n.
View Solution

