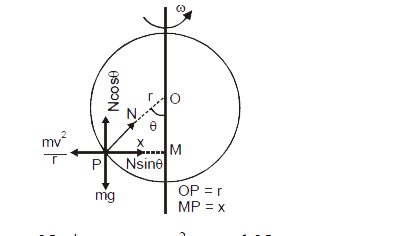
A circular loop has a small bead which can slide on it without friction. The radius of the loop is r. Keeping the loop vertically it is rotated about a vertical diameter at a constant angular speed ω. What is the value of angle θ, when the bead is in dynamic equilibrium ?
Centripetal force is provided by the horizontal component of the normal reaction N. The vertical component balances the weight. Thus
N sin θ=mω2x and N cosθ=mg
Also x = r sin θ⇒ N =mω2r
cos θ=gω2r or θ=cos−1(grω2)
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE -141videos
CIRCULAR MOTION
- BOOK - MOTIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE - 216videos
CIRCULAR MOTION
- BOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 4 Level-II20videos
CENTRE OF MASS
- BOOK - MOTIONCHAPTER - COMMUNICATION SYSTEMEXERCISE - EXERCISE - 36videos
COMMUNICATION SYSTEM
Similar Questions
A conducting circular loop of radius r is rotated about its diameter at a constant angular velocity ω in a magnetic field B perpendicular to the axis of rotation. In what position of the loop is the induced emf zero?
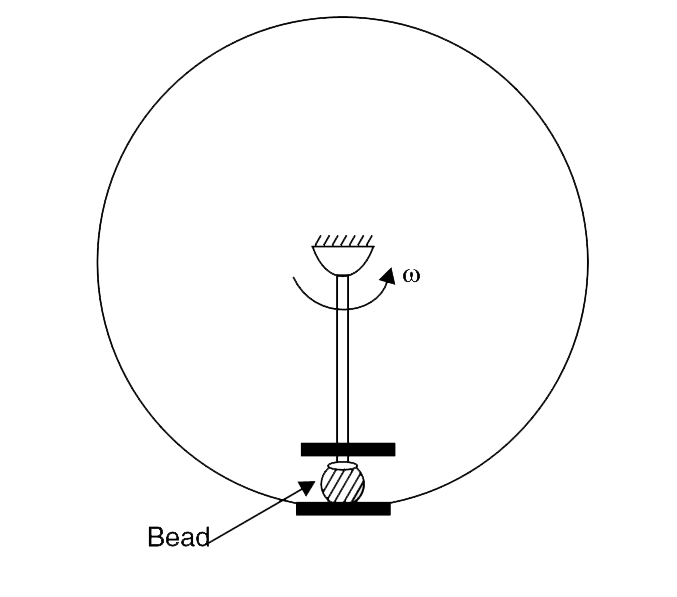
View SolutionA rigid mass less rod of length L is rotating in a vertical plane about a horizontal axis passing through one of its ends. At the other end of the rod there is a mass less metal plate welded to the rod. This plate supports a heavy small bead that can slide on the rod without friction. Just above the bead there is another identical metal plate welded to the rod. The bead remains confined between the plates. The gap between the plates is negligible compared to L. The angular speed of the rod when the bead is at lowest position of the circle is ω=2√gL. How many times a clink of the bead hitting a metal plate is heard during one full rotation of the rod ?
View Solution
Knowledge Check
- Question 1 - Select One or More
A circular loop is kept perpendicular to a uniform magnetic field. Loop is rotated about its diameter with constant angular velocity.
AMagnitude of emf induced will be minimum when magnitude of flux is maximumBMagnitude of emf is maximum when magnitude of flux is minimumCPhase difference between emf and flux is π2DNone of these - Question 2 - Select One
A very small circular loop of radius a is initially (at t = 0) coplanar and concentric with a much larger fixed circular loop of radius b. A constant current I flows in the larger loop. The smaller loop is rotated with a constant angular speed ω about the common diameter. The emf induced in the smaller loop as a function of time t is
Aπa2μ0I2bωcos(ωt)Bπa2μ0I2bωsin(ω2t2)Cπa2μ0I2bωsin(ωt)Dπa2μ0I2bωsin2(ωt) - Question 3 - Select One
A very small circular loop of radius a is initially (at t = 0) coplanar and concentric with a much larger fixed circular loop of radius b. A constant current I flows in the larger loop. The smaller loop is rotated with a constant angular speed ω about the common diameter. The emf induced in the smaller loop as a function of time t is
Aπa2μ0I2bωcosωtBπa2μ0I2bωsinω2t2Cπa2μ0I2bωsinωtDπa2μ0I2bωsin2ωt
A circular loop of metal wire of radius r is placed perpendicular to uniform magnetic field B. Half of the loop is folded about the diameter with constant angular velocity ω. If resistance of the loop is R then current in the loop is
View SolutionA ring of radius r is rotating about a vertical axis along its diameter with constant angular velocity ω.A read of mass m remains at rest w.r.t. ring at the position shown in figure. Then w2 is:
_2019_CBT8_E01_015_Q01.png)
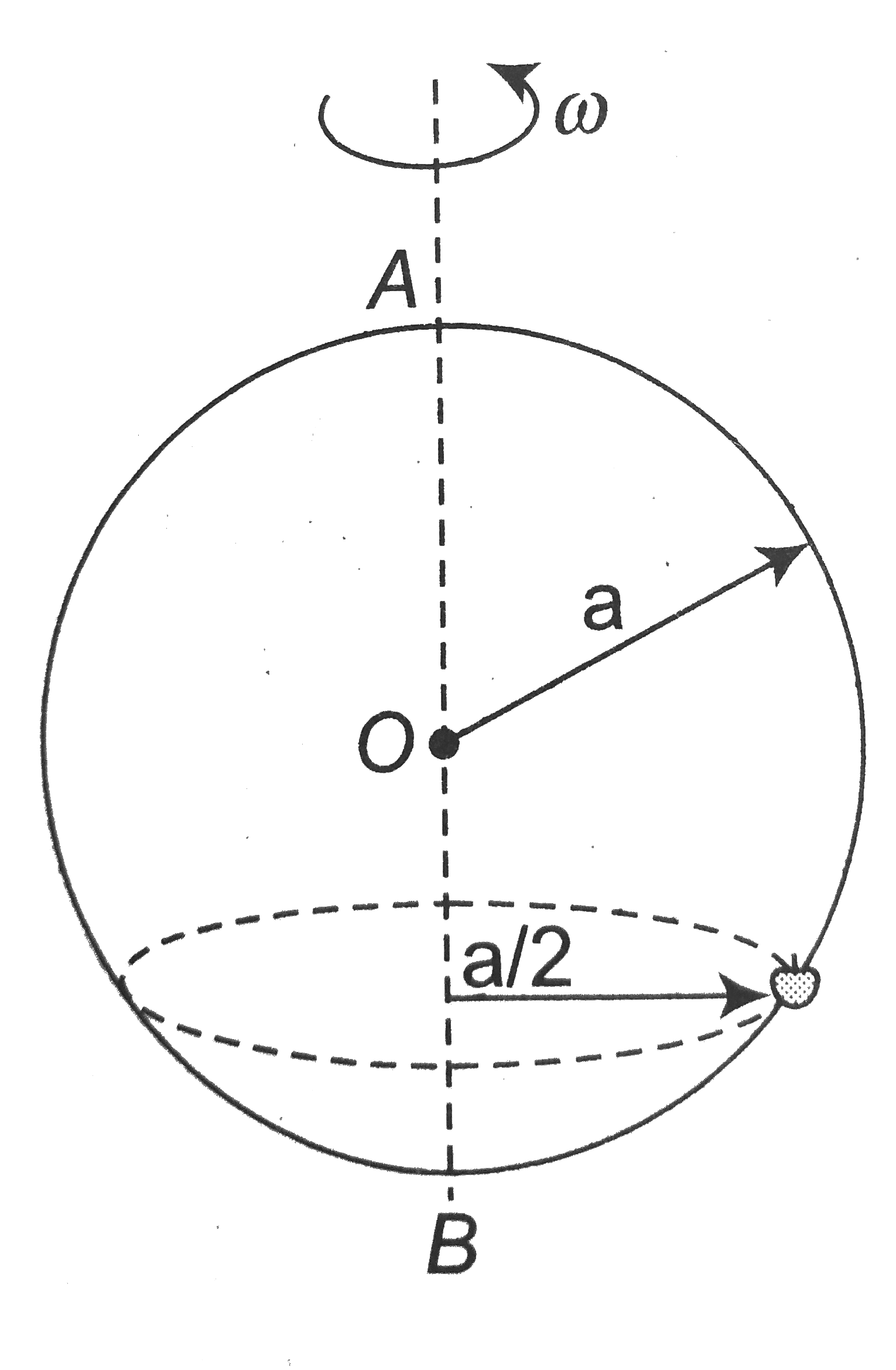
View SolutionA smooth wire is bent into a vertical circle of radius a. A bead P can slide smoothly on the wire. The circle is rotated about vertical diameter AB as axis with a speed omega as shown in figure. The bead P is at rest w.r.t. the circular ring in the position shown. then ω2 is equal to:
View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is
View SolutionA small bead of mass 'm' is threaded on a frictionless circulat wire of radius 'a' . The circule wire frame is rotated about its vertical diameter as shown. (assume acceleration due to grasvity is g) The angular speed required if the bead is to be made to move in a horizontal circle of radius a√32 is :
View Solution