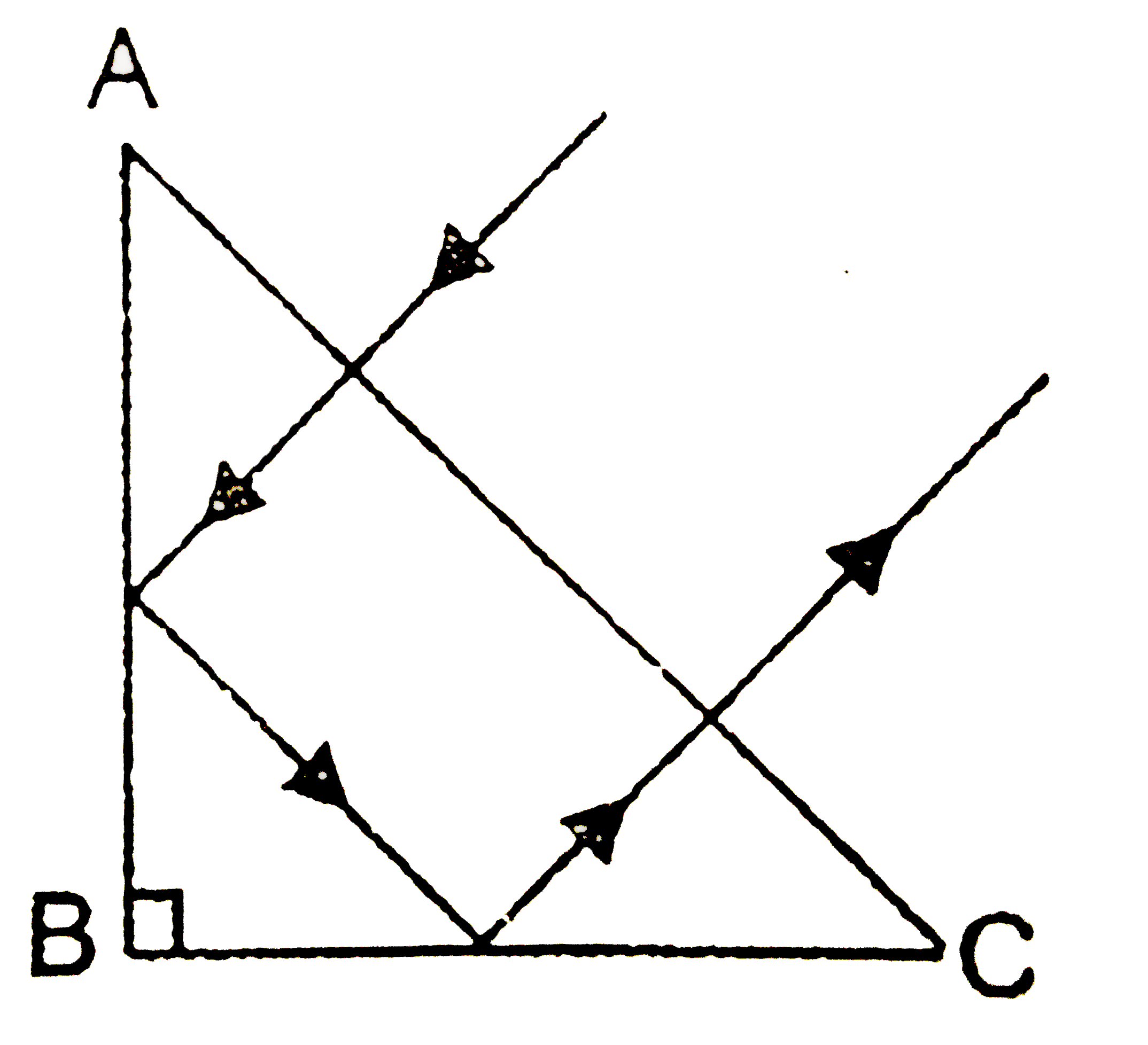
A ray falls on a prism ABC(AB=BC) and travels as shown in adjoining figure.The minimum refraction index of the prism material should be -
43558
√2
1.5
√3
The correct Answer is:B
To find the minimum refractive index of the prism material given that the ray falls on the prism ABC (where AB = BC), we can follow these steps:
1. Understanding the Geometry of the Prism:
- The prism ABC has equal sides AB and BC, which implies that it is an isosceles prism.
- The angles at A and C are equal, and we denote the angle at B as ∠ABC=θ.
2. Identifying the Angles:
- Since AB = BC, the angles at A and C are equal, and we can denote them as ∠A=∠C=180∘−θ2.
- For the minimum refractive index condition, we consider the critical angle for total internal reflection at point D.
3. Applying Snell's Law:
- At point D, where the ray undergoes total internal reflection, we can use Snell's law:
n1sin(θi)=n2sin(θr)
- Here, n1 is the refractive index of the prism, n2 is the refractive index of air (approximately 1), θi is the angle of incidence, and θr is the angle of refraction.
4. Critical Angle:
- The critical angle θc for total internal reflection is given by:
θc=sin−1(n2n1)
- For total internal reflection to occur, the angle of incidence must be greater than the critical angle.
5. Finding the Minimum Refractive Index:
- For the minimum refractive index, we set the critical angle θc=45∘:
sin(45∘)=1√2
- Substituting into the critical angle equation:
1√2=1n1
- Rearranging gives us:
n1=√2
6. Conclusion:
- Therefore, the minimum refractive index of the prism material should be √2.
Final Answer:
The minimum refractive index of the prism material should be √2.
- The prism ABC has equal sides AB and BC, which implies that it is an isosceles prism.
- The angles at A and C are equal, and we denote the angle at B as ∠ABC=θ.
- Since AB = BC, the angles at A and C are equal, and we can denote them as ∠A=∠C=180∘−θ2.
- For the minimum refractive index condition, we consider the critical angle for total internal reflection at point D.
- At point D, where the ray undergoes total internal reflection, we can use Snell's law:
n1sin(θi)=n2sin(θr)
- Here, n1 is the refractive index of the prism, n2 is the refractive index of air (approximately 1), θi is the angle of incidence, and θr is the angle of refraction.
- The critical angle θc for total internal reflection is given by:
θc=sin−1(n2n1)
- For total internal reflection to occur, the angle of incidence must be greater than the critical angle.
- For the minimum refractive index, we set the critical angle θc=45∘:
sin(45∘)=1√2
- Substituting into the critical angle equation:
1√2=1n1
- Rearranging gives us:
n1=√2
- Therefore, the minimum refractive index of the prism material should be √2.
The minimum refractive index of the prism material should be √2.
Topper's Solved these Questions
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:medical entrance special format question
Explore 23 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Medical entrance gallary
Explore 76 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Checkpoint 9.7
Explore 10 Videos
- NUCLEIBook:DC PANDEY ENGLISHChapter:NUCLEIExercise:C MADICAL ENTRANCES GALLERY
Explore 46 Videos
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
Similar Questions
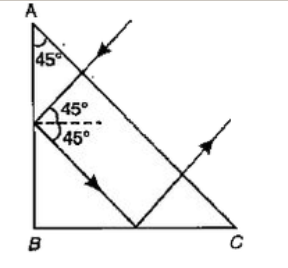
A ray of light falls on a right angled prism ABC (AB=BC) and travels as shown in figure. What is the refractive index of material of the prism ?
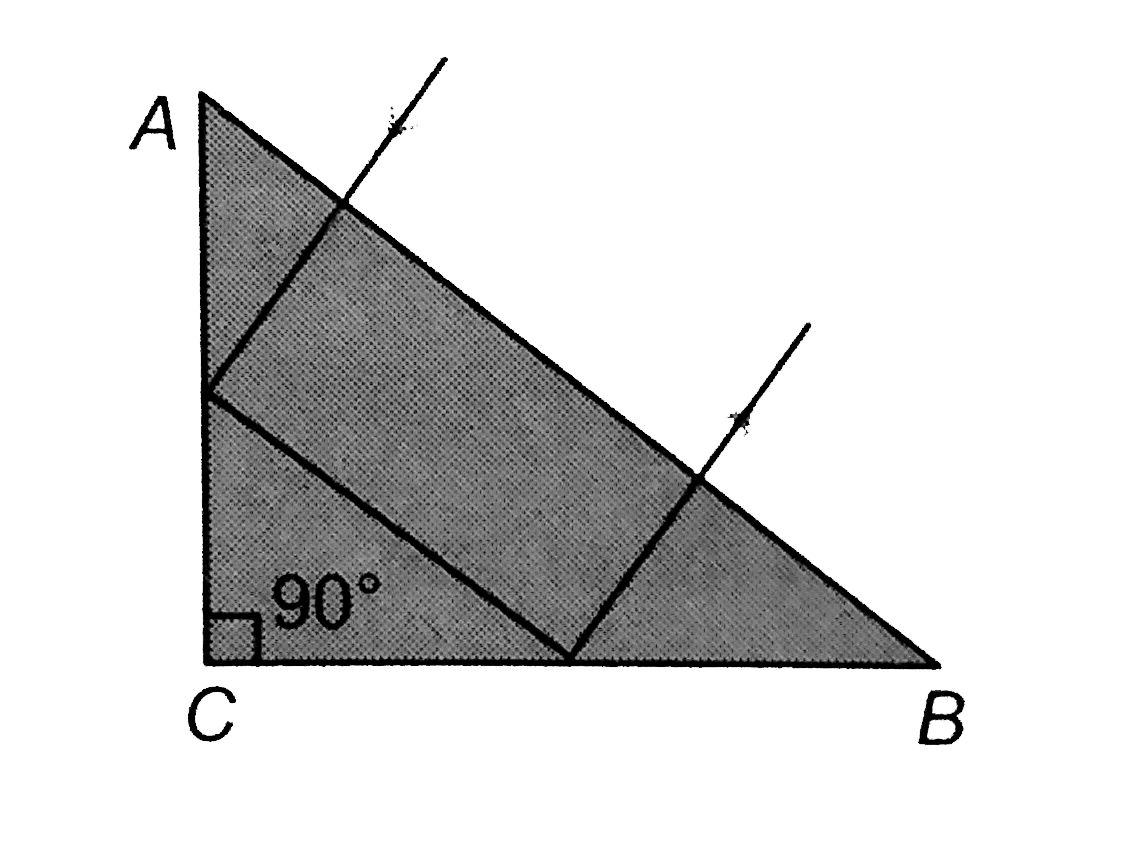
View SolutionA ray of light incident normally on an isosceles right angled prism travels as shown in the figure. The least value of the refractive index of the prism must be
View SolutionFind the angle of deviation suffered by the light ray shown in figure. The refractive index μ=2.0 for the prism material.
View Solution
A ray of light is incident normally on one face of a prism as shown in figure. The refractive index of the material of the prism is 53 and the prism is immersed in water of refractive index 43, then
View SolutionA ray LM of monochromatic light incident normally on one refracting surface AB of a regular glass prism ABC emerges in air from the adjacent surface C as shown in figure. Calculate the refractive index of the material of the prism.
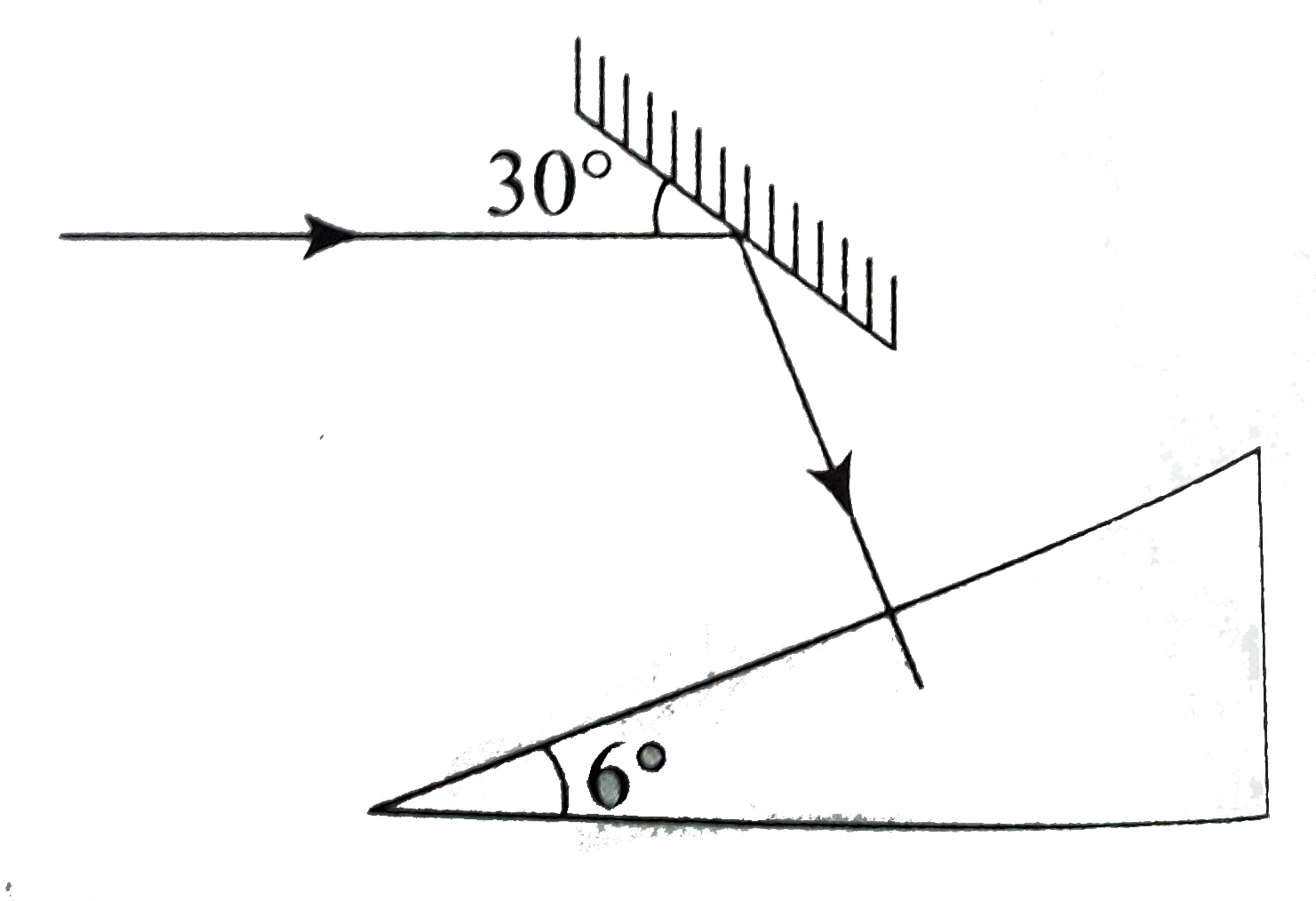
View SolutionFind the net deviation produced in the incident ray for the optical instrument shown in figure. (Take refractive index of the prism material as 2.)
View SolutionA ray of light LM incident normally on the surface AC of an isosceles right angled prism ABC (where AB = BC) emerges along PQ, parallel to LM, as shown in given figure.
What can you say about refractive index fe of the material of the prism?
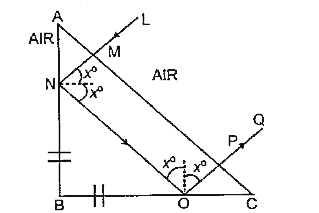
View SolutionA ray of light LM incident normally on the surface AC of an isosceles right angled prism ABC (where AB=BC) emerges along PQ, parallel to LM, as shown in given figure. What can you say about refractive index μ of the material of the prism ?
View SolutionAt what values fo the refractive index of a recantangular prism can a ray travel as shwon in figure. The section of the prism is an isoseless triangle and the ray in normally incident onto the face AC.
View SolutionA ray of light falls on an equilateral prism ABC as shown. Face AC of the prism is polished.

What is the refractive index μ of the material of the prims so that when the ray falls on face BC (after reflecting from AC) it makes an angle 60∘ with it.?
View Solution

