The dispersive powers of glasses of lenses used in an achromatic pair are in the ratio 5 : 3. If the focal length of the concave lens is 15 cm , then the nature and focal length of the other lens would be
convex, 9 cm
concave, 9 cm
convex, 25 cm
concave, 25 cm
The correct Answer is:A
To solve the problem step by step, we will follow the concepts of dispersive power and the formula for an achromatic lens pair.
Step 1: Understand the Given Information
We have two lenses in an achromatic pair. The dispersive powers of the lenses are in the ratio of 5:3. We denote the dispersive power of the first lens (concave lens) as ω1=5x and the second lens (unknown) as ω2=3x. The focal length of the concave lens is given as f1=−15cm.
Step 2: Use the Formula for Achromatic Pair
The formula for an achromatic pair of lenses is given by:
ω1f1+ω2f2=0
Substituting the values we have:
5x−15+3xf2=0
Step 3: Simplify the Equation
Rearranging the equation gives:
3xf2=5x15
We can simplify 5x15 to x3:
3xf2=x3
Step 4: Solve for f2
Now, we can cross-multiply to solve for f2:
3x⋅3=x⋅f2
This simplifies to:
9x=x⋅f2
Assuming x≠0, we can divide both sides by x:
f2=9cm
Step 5: Determine the Nature of the Lens
Since f2 is positive, the lens is a convex lens.
Final Answer
The nature of the other lens is convex, and its focal length is 9cm.
We have two lenses in an achromatic pair. The dispersive powers of the lenses are in the ratio of 5:3. We denote the dispersive power of the first lens (concave lens) as ω1=5x and the second lens (unknown) as ω2=3x. The focal length of the concave lens is given as f1=−15cm.
The formula for an achromatic pair of lenses is given by:
ω1f1+ω2f2=0
Substituting the values we have:
5x−15+3xf2=0
Rearranging the equation gives:
3xf2=5x15
We can simplify 5x15 to x3:
3xf2=x3
Now, we can cross-multiply to solve for f2:
3x⋅3=x⋅f2
This simplifies to:
9x=x⋅f2
Assuming x≠0, we can divide both sides by x:
f2=9cm
Since f2 is positive, the lens is a convex lens.
The nature of the other lens is convex, and its focal length is 9cm.
Topper's Solved these Questions
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:medical entrance special format question
Explore 23 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Medical entrance gallary
Explore 76 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Checkpoint 9.7
Explore 10 Videos
- NUCLEIBook:DC PANDEY ENGLISHChapter:NUCLEIExercise:C MADICAL ENTRANCES GALLERY
Explore 46 Videos
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
Similar Questions
Find the focal length of the lens used.
View SolutionThe focal length of a plano-concave lens is -10 cm , then its focal length when its palne surface is polished is
View SolutionIf the focal length of the objective lens is increased then Magnifying power
View SolutionIf the focal length of objective lens is increased then magnifying power of
View SolutionTwo lenses are placed in contact with each other and the focal length of combination is 80cm. If the focal length of one is 20cm, then the power of the other will be
View SolutionThe dispersive power of the material of a lens is 0.04 and the focal length of the lens is 10cm. Find the difference in the focal length (in mm) of the lens for violet and red colour.
View SolutionThe figure below shows the positions of a point object 0, two lenses, a plane mirror and the final image I which coincides with the object. The focal length of the convex lens is 20 cm. Calculate the focal length of the concave lens.
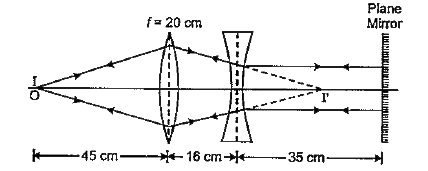
View SolutionThe length of the compound microscope is 14cm. The magnifying power for relaxed eye is 25. If the focal length of eye lens is 5cm, then the object distance for objective lens will be
View SolutionA convex lens of focal length A and a concave lens of focal length B are placed in contact. The focal length of the combination is
View SolutionAn achromatic lens-doublet is formed by placing in contact a convex lens of focal length 20cm and a concave lens of focal length 30cm. The dispersive power of the material of the convex lens is 0.8. Determine the dispersive power of the material of the concave lens. Calculate the focal length of the lens-doublet.
View Solution

