In a uniform magnetic field, a shaped metal frame is located perpendicular to the plane of the conductor and varying with time at the rate . A conducting connector starts moving with an acceleration along the parallel bars of the frame. The length of the connector is equal to l = 44 cm. Find the emf induced in the loop t = 1 s after the beginning of the motion, if at the moment t = 0, the loop area and the magnetic induction are equal to zero.
To find the induced EMF in the loop at t=1 second, we will follow these steps:
Step 1: Determine the displacement of the connector
The connector starts from rest and moves with a constant acceleration a=30cm/s2=0.3m/s2. The displacement x after time t can be calculated using the equation of motion:
x=ut+12at2
Since the initial velocity u=0:
x=12at2=12×0.3m/s2×(1s)2=0.15m
Step 2: Calculate the area of the loop
The area A of the loop formed by the connector can be calculated as:
A=x⋅l
where l=0.44m (length of the connector):
A=0.15m×0.44m=0.066m2
Step 3: Calculate the change in magnetic flux
The magnetic flux Φ through the loop is given by:
Φ=B⋅A
The magnetic field B is varying with time at the rate of dBdt=0.20T/s. The change in magnetic field B after t=1 second is:
B=dBdt⋅t=0.20T/s⋅1s=0.20T
Thus, the magnetic flux at t=1 second is:
Φ=B⋅A=0.20T⋅0.066m2=0.0132Wb
Step 4: Calculate the induced EMF
The induced EMF E can be calculated using Faraday's law of electromagnetic induction:
E=−dΦdt
To find dΦdt, we note that both B and A are functions of time:
dΦdt=AdBdt+BdAdt
Since A=x⋅l and x=12at2, we have:
dAdt=l⋅dxdt=l⋅(at)=0.44m⋅(0.3m/s2⋅1s)=0.044m2/s
Now substituting the values:
dΦdt=A⋅dBdt+B⋅dAdt=0.066m2⋅0.20T/s+0.20T⋅0.044m2/s
Calculating each term:
=0.0132+0.0088=0.022Wb/s
Thus, the induced EMF is:
E=−dΦdt=−0.022V=0.022V (taking the magnitude)
Final Answer
The induced EMF in the loop at t=1 second is approximately 0.022V or 22mV.
---
The connector starts from rest and moves with a constant acceleration a=30cm/s2=0.3m/s2. The displacement x after time t can be calculated using the equation of motion:
x=ut+12at2
Since the initial velocity u=0:
x=12at2=12×0.3m/s2×(1s)2=0.15m
The area A of the loop formed by the connector can be calculated as:
A=x⋅l
where l=0.44m (length of the connector):
A=0.15m×0.44m=0.066m2
The magnetic flux Φ through the loop is given by:
Φ=B⋅A
The magnetic field B is varying with time at the rate of dBdt=0.20T/s. The change in magnetic field B after t=1 second is:
B=dBdt⋅t=0.20T/s⋅1s=0.20T
Thus, the magnetic flux at t=1 second is:
Φ=B⋅A=0.20T⋅0.066m2=0.0132Wb
The induced EMF E can be calculated using Faraday's law of electromagnetic induction:
E=−dΦdt
To find dΦdt, we note that both B and A are functions of time:
dΦdt=AdBdt+BdAdt
Since A=x⋅l and x=12at2, we have:
dAdt=l⋅dxdt=l⋅(at)=0.44m⋅(0.3m/s2⋅1s)=0.044m2/s
Now substituting the values:
dΦdt=A⋅dBdt+B⋅dAdt=0.066m2⋅0.20T/s+0.20T⋅0.044m2/s
Calculating each term:
=0.0132+0.0088=0.022Wb/s
Thus, the induced EMF is:
E=−dΦdt=−0.022V=0.022V (taking the magnitude)
The induced EMF in the loop at t=1 second is approximately 0.022V or 22mV.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point
60 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Taking it together
119 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 Subjective
20 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
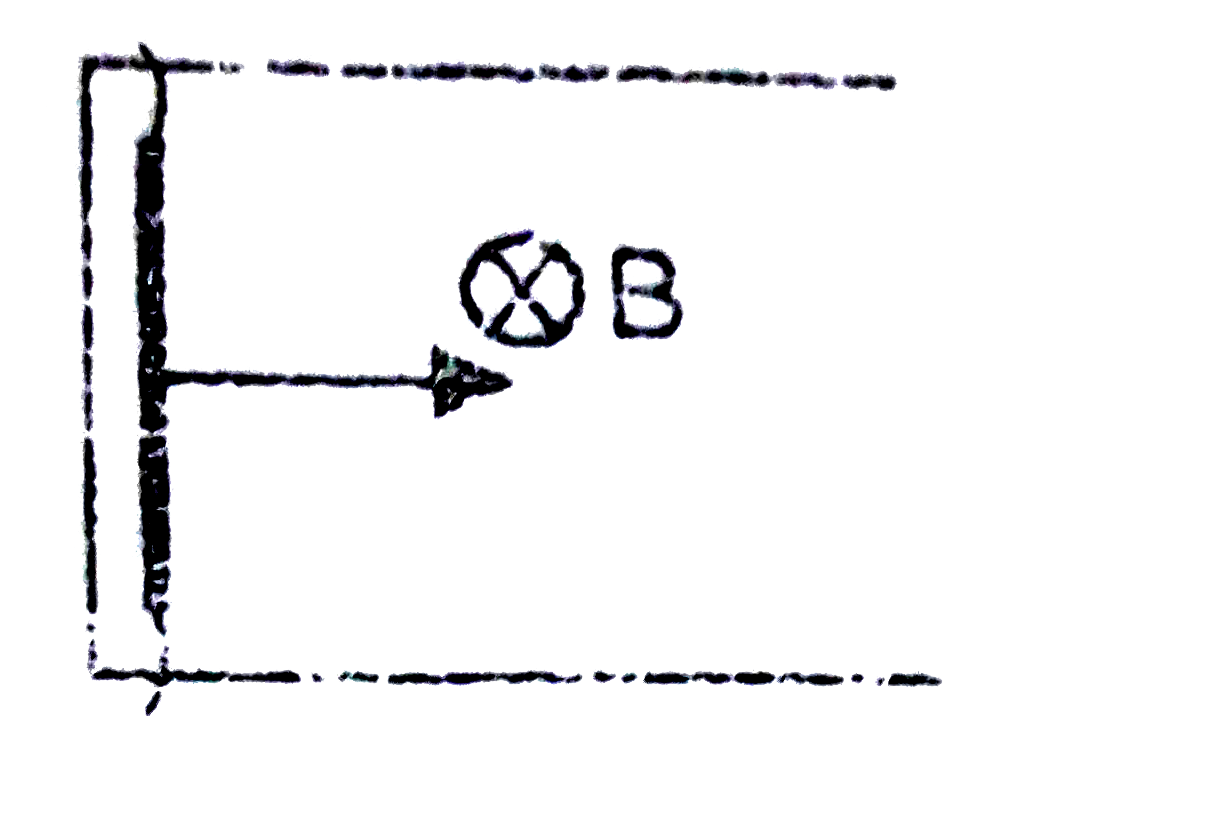
A II-shaped conductor is located in a uniform magnetic field perpendicular to the plane of the conductor and varying with time at the rate dBdt=0.10T/s.A conducting connectors starts moving with a constant acceleration w=10cm/s2 along the parallel bars of the conductor.The length of the connector is equal to l=20cm.Find the emf induced (in mV) in the loop t=2.0s after the beginning of the motion.If at the moment t=0 the loop area and the magnetic induction (B) are equal to zero.The self inductance of the loop is to be neglected.
View SolutionA rectangular conductor LMNO is place in a uniform magnetic field of 0.5 T Fig. The field is directed perpendicular to the plane to the conductor. When the arm MN of length 20 cm is moved with a velocity of 10 m/s calculate the emf induced in the arm. Find the value of induced current if resistance of arm MN is 5 Ohm

View Solution
Knowledge Check
The magnetic flux through a coil perpendicluar to its plane and directed into paper is varying according to the relation ϕ=(2t2+4t+6)mWb. The emf induced in the loop at t=4 s is
A0.12 VB2.4 VC0.02 VD1.2 V
A conducting rod of unit length moves with a velocity of 5m/s in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.4T. Find the emf induced between the ends of the stick.
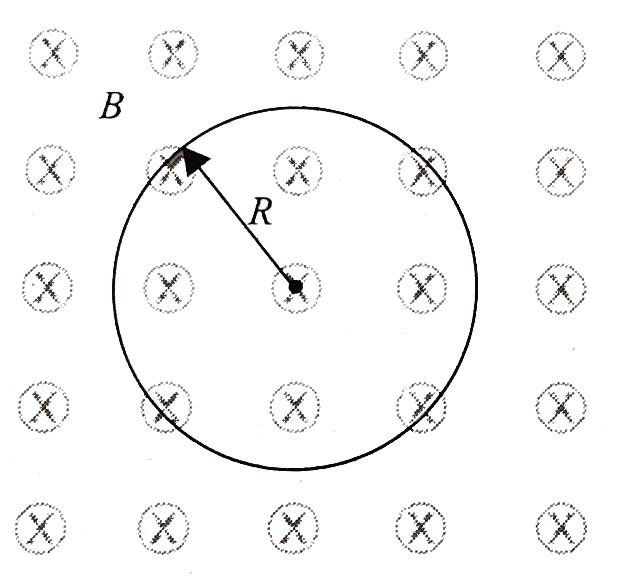
View SolutionA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is
View SolutionA rectangular loop with a sliding conductor of length l is located in a uniform magnetic field perpendicular to the plane of loop. The magnetic induction perpendicular to the plane of loop Is equal to B. The part ad and be has electric resistance R1 and R2, respectively. The conductor starts moving with constant acceleration a0, at time t=0. Neglecting the self-inductance of the loop and resistance of conductor. Find
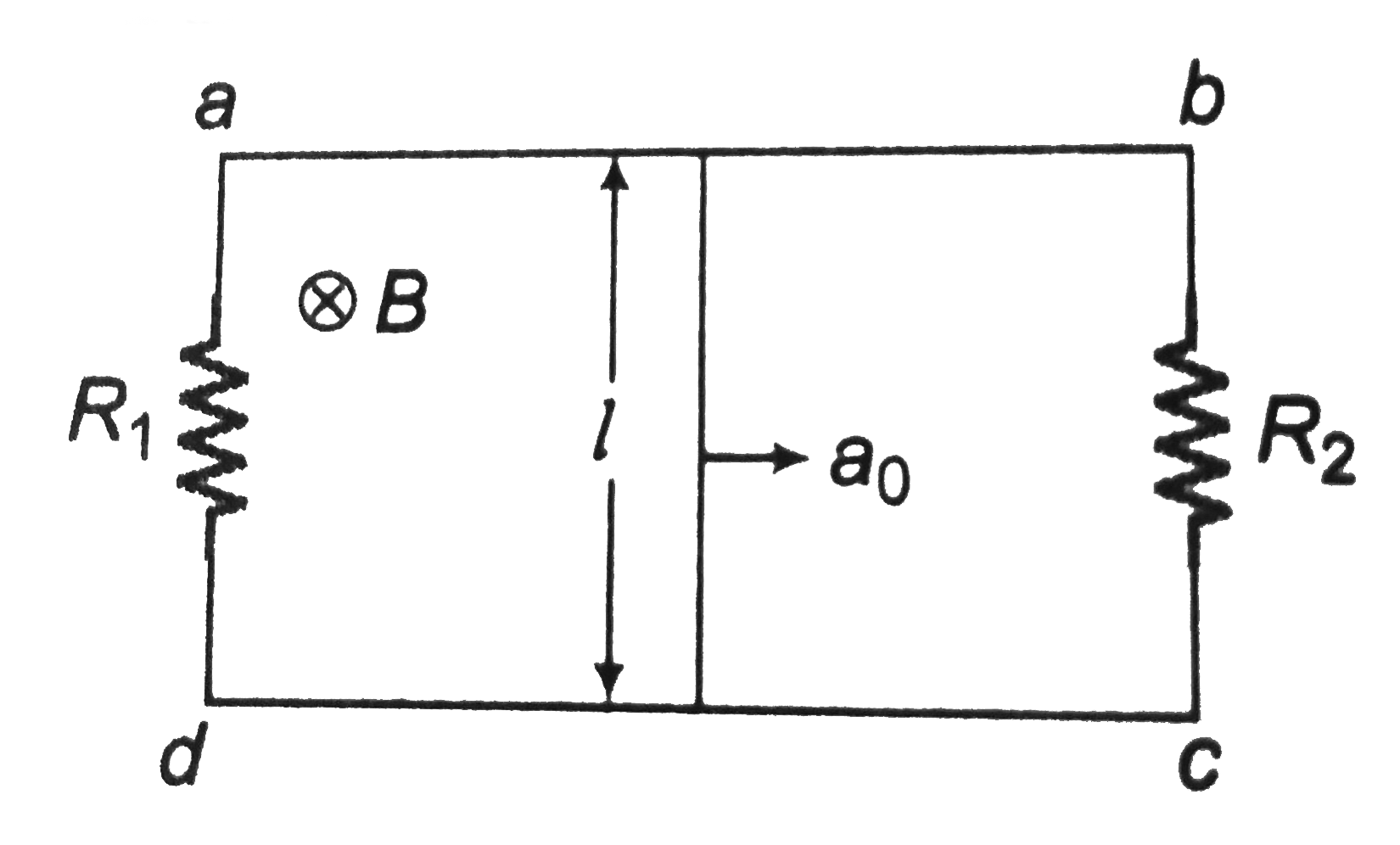
(a) the current through the conductor during its motion.
(b) the polarity of abcd terminal.
(c) external force required to move the conductor with the given acceleration.
View SolutionA conducting circular loop is in a perpendicular magnetic field of induction 10−2T If the radius of the loop starts shrinking at a uniform rate of 1 mm/s, then the e.m.f. induced in the loop at the instant when its radius is 10 cm will be
View SolutionA conducintg circular loop having a redius of 5.0cm, is placed perpendicular to a magnetic field of 0.50 T. It is removed from the field in 0.50 s. Find the average emf produced In the loop during this time.
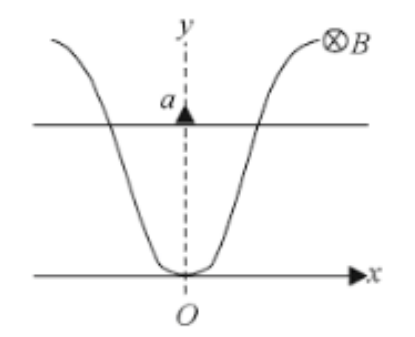
View SolutionA wire bent as a parabola y=kx2 is located in a uniform magnetic field of induction B, the vector B being perpendicular to the plane xy. At t=0, the sliding wire starts sliding from the vertex O with a constant acceleration a linearly as shown in Fig. Find the emf induced in the loop -
View SolutionA conducting square loop is placed in a magnetic field B with its plane perpendicular to the field. Now the sides of the loop start shrinking at a constant rate α. the induced emf in the loop at an instant when its side is a is
View Solution
