A ring of radius 2m translates in its plane with a constant velocity 5m/s. A uniform magnetic field 0.1 T exists in the space in a direction perpendicular to the plane of the ring. Consider different pairs of diametrically opposite points on the ring.
(i) Between which pair of points is emf maximum? What is the value of this maximum emf?
(ii) Between which pair of points is the emf minimum? What is the value of this minimum emf?
To solve the problem, we will analyze the situation step by step.
Given Data:
- Radius of the ring, R=2m
- Velocity of the ring, V=5m/s
- Magnetic field, B=0.1T
Step 1: Understanding the EMF in the Ring
The electromotive force (EMF) induced in a moving conductor in a magnetic field can be calculated using the formula:
EMF=VBLsin(θ)
where:
- V is the velocity of the conductor,
- B is the magnetic field strength,
- L is the length of the conductor within the magnetic field,
- θ is the angle between the velocity vector and the magnetic field vector.
Step 2: Maximum EMF Calculation
To find the maximum EMF, we need to identify the pair of diametrically opposite points where the angle θ is 90∘ (i.e., sin(90∘)=1).
1. Choosing Points for Maximum EMF:
- Let’s consider points M and N that are diametrically opposite on the ring.
- The length L between these points is equal to the diameter of the ring, which is 2R=2×2=4m.
2. Calculating Maximum EMF:
EMFmax=V⋅B⋅L
Substituting the values:
EMFmax=5m/s⋅0.1T⋅4m=2V
Step 3: Minimum EMF Calculation
To find the minimum EMF, we need to identify the pair of diametrically opposite points where the angle θ is 0∘ or 180∘ (i.e., sin(0∘)=0 or sin(180∘)=0).
1. Choosing Points for Minimum EMF:
- Let’s consider points P and Q that are also diametrically opposite on the ring but aligned with the direction of motion of the ring.
2. Calculating Minimum EMF:
EMFmin=V⋅B⋅L⋅sin(0∘)=0
Since the direction of L (the line connecting P and Q) is parallel to the velocity V, the EMF is zero.
Final Answers:
(i) The maximum EMF is between points M and N and its value is 2V.
(ii) The minimum EMF is between points P and Q and its value is 0V.
- Radius of the ring, R=2m
- Velocity of the ring, V=5m/s
- Magnetic field, B=0.1T
The electromotive force (EMF) induced in a moving conductor in a magnetic field can be calculated using the formula:
EMF=VBLsin(θ)
where:
- V is the velocity of the conductor,
- B is the magnetic field strength,
- L is the length of the conductor within the magnetic field,
- θ is the angle between the velocity vector and the magnetic field vector.
To find the maximum EMF, we need to identify the pair of diametrically opposite points where the angle θ is 90∘ (i.e., sin(90∘)=1).
- Let’s consider points M and N that are diametrically opposite on the ring.
- The length L between these points is equal to the diameter of the ring, which is 2R=2×2=4m.
EMFmax=V⋅B⋅L
Substituting the values:
EMFmax=5m/s⋅0.1T⋅4m=2V
To find the minimum EMF, we need to identify the pair of diametrically opposite points where the angle θ is 0∘ or 180∘ (i.e., sin(0∘)=0 or sin(180∘)=0).
- Let’s consider points P and Q that are also diametrically opposite on the ring but aligned with the direction of motion of the ring.
EMFmin=V⋅B⋅L⋅sin(0∘)=0
Since the direction of L (the line connecting P and Q) is parallel to the velocity V, the EMF is zero.
(i) The maximum EMF is between points M and N and its value is 2V.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point
60 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Taking it together
119 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 Subjective
20 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A circular copper ring of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the space in a direction perpendicular of the plane o the ring. Consider different pairs of diametrically opposite points on the ring. (a) Between which pair of points is the emf? (b) Between which pair of points is the emf minimum? What is the value of this minimum emf?
View SolutionA ring of radius R is rolling on a horizontal plane with constant velocity v. There is a constant and uniform magnetic field B which is perpendicular to the plane of the ring. Emf across the lowest point A and right-most point C as shown in the figure will

View Solution
Knowledge Check
A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
Ait is rotated about its axis.Bit is rotated about its diameter.Cit is not moved.Dit is given translational motion in the field.
A copper wire bent in the shape of a semicircle of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the direction perpendicular to the plane of the wire. Find the emf induced between the ends of the wire if (a) the velocity is perpendicular ot the diameter joining free ends, (b) the velocity is parallel to this diameter.
View SolutionA 20 cm long conducting rod is set into pure translation with a uniform velocity of 10cm s ^(-1) perpendicular to its length. A uniform magnetic field of magnitude 0.10 T exists in a direction perpendicular to the plane of motion. Find emf developed in the rod.
View SolutionA copper disc of radius 0.1 m is rotated about its natural axis with 10 rps in a uniform magnetic field of 0.1 T with its plane perpendicular to the field, The emf induced across the radius of the disc is
View SolutionA vertical conducting ring of radius R falls vertically with a speed V in a horizontal uniform magnetic field B which is perpendicular to the plane of the ring. Which of the following statements is correct?
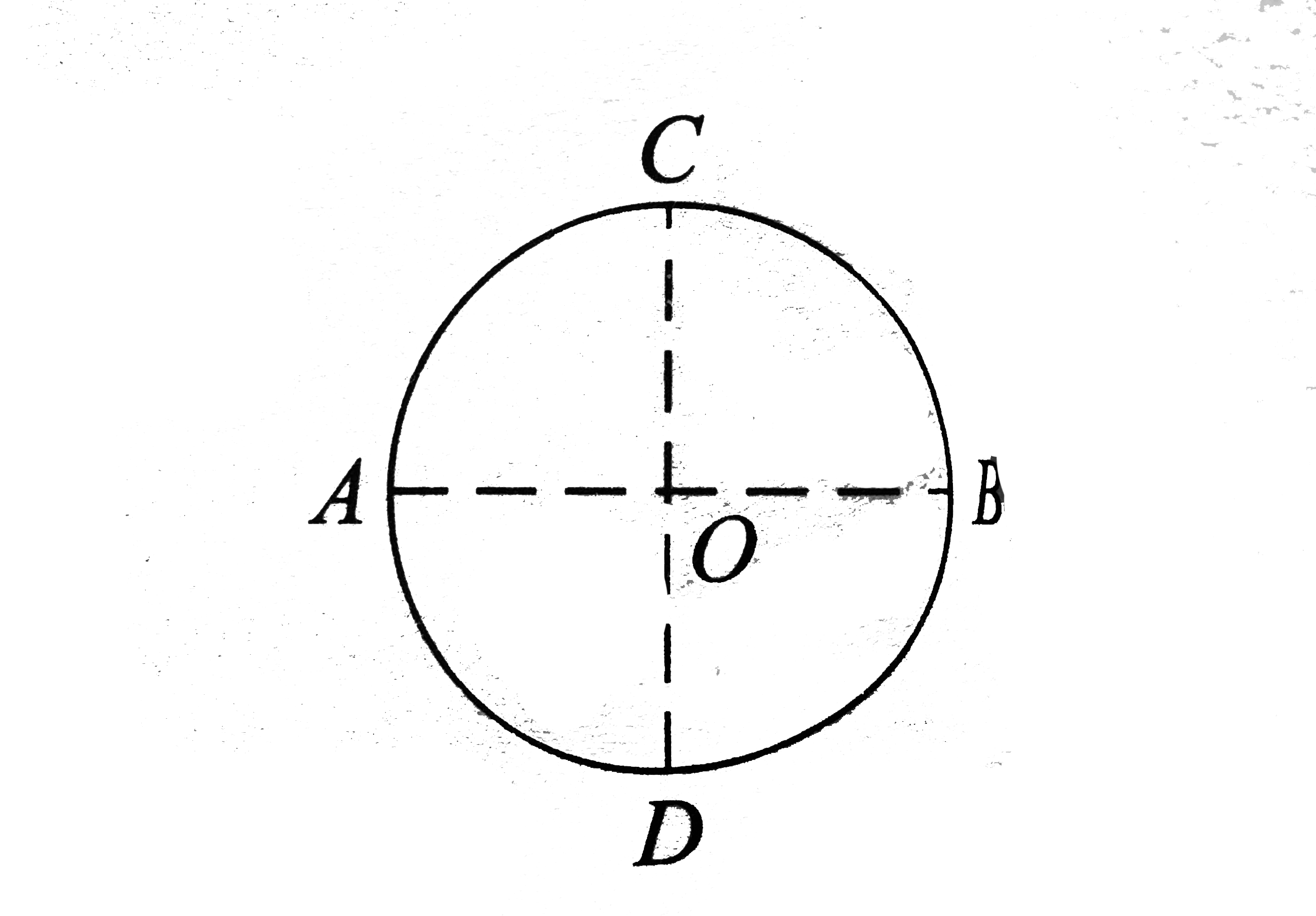
View Solution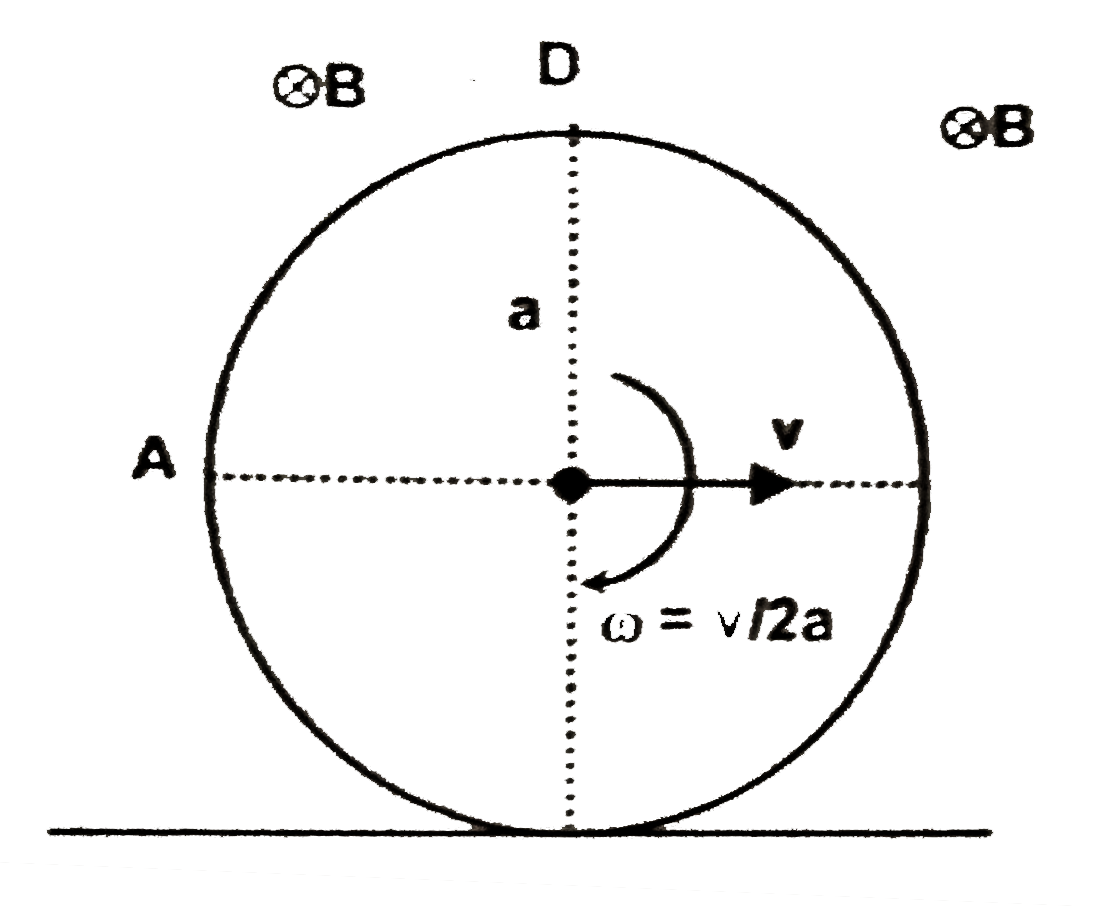
A circular conducting ring of radius 'a' is rolling with slipping on a horizontal surface as shown. A uniform magnetic field B is existing perpendicular to the plane of motion of the ring. The emf iniduced between the points A and D of the ring is
View SolutionA ring of radius R moves with a velocity v in a uniform static magnetic field B as shown in diagram. The emf between P and Q is
View SolutionA semicircle conducting ring of radius R is placed in the xy plane, as shown in Fig. A uniform magnetic field is set up along the x-axis. No emf, will be induced in the ring if

View Solution
