The current in an ideal, long solenoid is varied at a uniform rate of 0.02A/s. The solenoid has 1000 turns/m and its radius is 8 cm.
(i) Consider a circle of radius 2 cm inside the solenoid with its axis coinciding with the axis of the solenoid. Write the change in the magnetic flux through this circle in 4 s.
(ii) Find the electric field induced at a point on the circumference of the circle.
(iii) Find the electric field induced at a point outside the solenoid at a distance 9 cm from its axis.
To solve the problem step by step, we will break it down into three parts as per the question.
Given Data:
- Rate of change of current, dIdt=0.02A/s
- Number of turns per unit length of the solenoid, n=1000turns/m
- Radius of the solenoid, R=8cm=0.08m
- Radius of the circle inside the solenoid, r=2cm=0.02m
- Time interval, t=4s
(i) Change in Magnetic Flux through the Circle in 4 s
1. Calculate the change in current (dI):
dI=dIdt×t=0.02A/s×4s=0.08A
2. Calculate the magnetic field (B) inside the solenoid:
The magnetic field inside a solenoid is given by:
B=μ0nI
where μ0=4π×10−7T m/A.
3. Calculate the change in magnetic field (dB):
dB=μ0ndI=(4π×10−7)×1000×0.08
4. Calculate the area (A) of the circle:
A=πr2=π(0.02)2=π×0.0004=0.0004πm2
5. Calculate the change in magnetic flux (dΦ):
dΦ=dB×A=(4π×10−7×1000×0.08)×(0.0004π)
dΦ=1.263×10−7Wb
(ii) Electric Field Induced at a Point on the Circumference of the Circle
1. Use Faraday's law of electromagnetic induction:
The induced EMF (ε) is given by:
ϵ=−dΦdt
Since we are looking for the average electric field (E) around the circumference, we can write:
E⋅2πr=ϵ
2. Calculate the induced EMF:
ϵ=dΦdt=1.263×10−74=3.1575×10−8V
3. Calculate the electric field (E):
E⋅2π(0.02)=3.1575×10−8
E=3.1575×10−82π(0.02)=2.5×10−7V/m
(iii) Electric Field Induced at a Point Outside the Solenoid at a Distance of 9 cm
1. Use Faraday's law again:
The electric field at a distance r=0.09m (9 cm) from the axis of the solenoid:
E⋅2π(0.09)=dΦdt
2. Calculate the area of the solenoid:
The area is given by:
A=πR2=π(0.08)2=π×0.0064=0.0064πm2
3. Calculate the electric field (E):
E⋅2π(0.09)=μ0ndIdt⋅A
E⋅2π(0.09)=(4π×10−7)⋅1000⋅0.02⋅(0.0064π)
E=(4π×10−7)⋅1000⋅0.02⋅(0.0064π)2π(0.09)
E=8.9×10−7V/m
Final Answers:
- (i) Change in magnetic flux through the circle in 4 s: 1.263×10−7Wb
- (ii) Electric field induced at a point on the circumference of the circle: 2.5×10−7V/m
- (iii) Electric field induced at a point outside the solenoid at a distance of 9 cm: 8.9×10−7V/m
- Rate of change of current, dIdt=0.02A/s
- Number of turns per unit length of the solenoid, n=1000turns/m
- Radius of the solenoid, R=8cm=0.08m
- Radius of the circle inside the solenoid, r=2cm=0.02m
- Time interval, t=4s
dI=dIdt×t=0.02A/s×4s=0.08A
The magnetic field inside a solenoid is given by:
B=μ0nI
where μ0=4π×10−7T m/A.
dB=μ0ndI=(4π×10−7)×1000×0.08
A=πr2=π(0.02)2=π×0.0004=0.0004πm2
dΦ=dB×A=(4π×10−7×1000×0.08)×(0.0004π)
dΦ=1.263×10−7Wb
The induced EMF (ε) is given by:
ϵ=−dΦdt
Since we are looking for the average electric field (E) around the circumference, we can write:
E⋅2πr=ϵ
ϵ=dΦdt=1.263×10−74=3.1575×10−8V
E⋅2π(0.02)=3.1575×10−8
E=3.1575×10−82π(0.02)=2.5×10−7V/m
The electric field at a distance r=0.09m (9 cm) from the axis of the solenoid:
E⋅2π(0.09)=dΦdt
The area is given by:
A=πR2=π(0.08)2=π×0.0064=0.0064πm2
E⋅2π(0.09)=μ0ndIdt⋅A
E⋅2π(0.09)=(4π×10−7)⋅1000⋅0.02⋅(0.0064π)
E=(4π×10−7)⋅1000⋅0.02⋅(0.0064π)2π(0.09)
E=8.9×10−7V/m
- (i) Change in magnetic flux through the circle in 4 s: 1.263×10−7Wb
- (ii) Electric field induced at a point on the circumference of the circle: 2.5×10−7V/m
- (iii) Electric field induced at a point outside the solenoid at a distance of 9 cm: 8.9×10−7V/m
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point
60 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Taking it together
119 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 Subjective
20 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
The magnetic flux linked with a vector area →A in a uniform magnetic field →B is
View SolutionL, C and R represent the physical quantities, inductance, capacitance and resistance respectively. The combination(s) which have the dimensions of frequency are
View SolutionA rectangular loop with a sliding connector of length l is located in a uniform magnetic field perpendicular to the loop plane. The magnetic induction is equal to B. The connector has an electric resistance R, the sides ab and cd have resistances R1 and R2. Neglecting the self-inductance of the loop, find the current flowing in the connector during its motion with a constant velocity v.
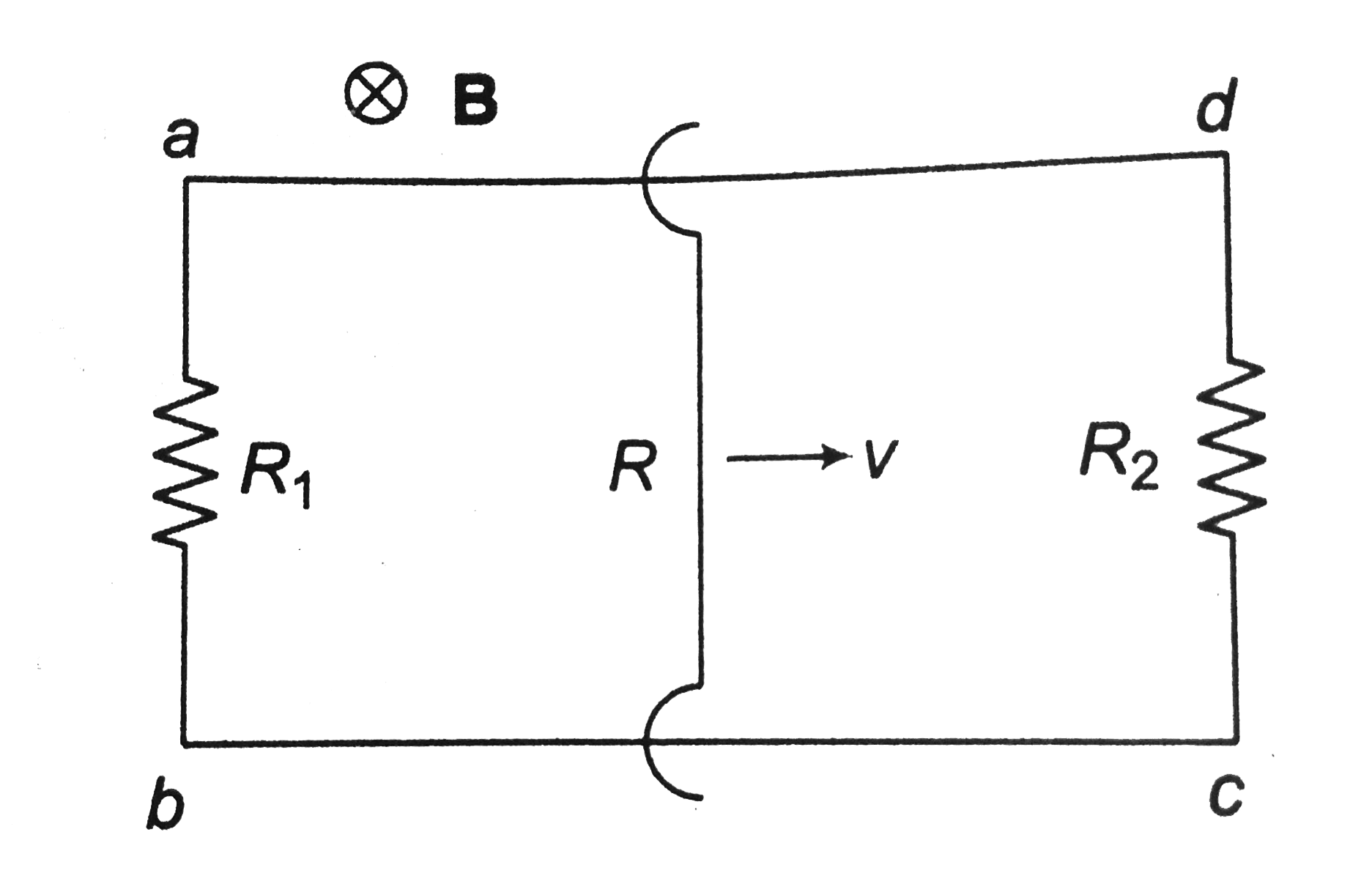
View SolutionA potentiometer wire is 100cm long hand a constant potential difference is maintained across it. Two cells are connected in series first to support one another and then in opposite direction. The balance points are obatined at 50cm and 10cm from the positive end of the wire in the two cases. The ratio of emfs is:
View SolutionOut of the following options which one one can be used to produce a propaagating electromagnetic wave?
View SolutionThe current in an ideal, long solenoid is varied at a uniform rate of 0.01As−1. The solenoid has 2000 turns/m and its radius 6.0 cm. (a) Consider a circle of radius 1.0 cm inside the solenoid with its axis coinciding with the axis of the solenoid. write the change in the magnetic flux through this circle in 2.0 seconds. (b) find the electric field induced at a point on the circumference of the circle. (c) find the electric field induced at a point outside the solenoid at a distance 8.0cm from its axis.
View SolutionStatement I: An emf is induced ina long solenoid by a bar magnet that moves while totally inside the solenoid along axis of the solenoid. Statement II: as the magnet moves inside the solenoid the flux through turns of the solenoid changes.
View SolutionAn air-solenoid has 500 turns of wire in its 40 cm length. If the current in the wire be 1.0 ampere then the magnetic field on the axis inside the solenoid is -
View SolutionA long solenoid of radius 4 cm, length 400 cmcarries a current of 3 A. The total number of turns is 100. Assuming ideal solenoid, find the flux passing through a circular surface having centre on axis of solenoid of radius 3 cm and is perpendicular to the axis of solenoid (i) inside and (ii) at the end of solenoid.
View SolutionThe cruuent in an ideal, long solenoid is varied at a uniform rate of 0.02A/s. The solenoid has 1000 turns/s and its radius is 8 cm.
(i) Consider a circle of radius 2 cm inside the solenoid with its axis coinciding with the axis of the solenoid. Write the change in the magnetic flux through this circle in 4 s.
(ii) Find the electric field induced at a point on the circumference of the circle.
(iii) Find the electric field induced at a point outside the solenoid at a distance 9 cm from its axis.
View SolutionA solenoid of length 0.6 m has a radius of 2 cm and is made up of 600 turns If it carries a current of 4 A, then the magnitude of the magnetic field inside the solenoid is
View SolutionA long solenoid of radius 4 cm, length 400 cm carries a current of 3A. The total number of turns is 100. Assuming ideal solenoid, find the flux passing through a circular surface having centre on axis of solenoid of radius 3cm and is perpendicular to the axis of solenoid in side.
View SolutionThe magnetic field within a long, straight solenoid with a circular cross - section of radius r is (as shown) increasing at a rate of alpha . The rate of change of flux through a circle with radius a inside the solenoid and with centre on the solenoid axis is
View SolutionA solenoid length 0.4cm, radius 1 cm and 400 turns of wire. If a current of 5 A is passed through this solenoid, what is the magnetic field inside the solenoid ?
View SolutionA 0.100 m long solenoid has a radius of 0.050 m and 1.50×104 turns. The current in the solenoid changes at a rate of 6.0 A/s. A conducting loop of radius 0.0200 m is placed at the center of the solenoid with its axis the same as that of the solenoid as shown.
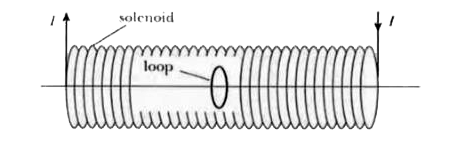
Determine the mutual inductance of this combination.
View Solution
