A mass is suspended separately by two springs of spring constants $k_{1}$ and $k_{2}$ in successive order. The time periods of oscillations in the two cases are $T_{1}$ and $T_{2}$ respectively. If the same mass be suspended by connecting the two springs in parallel, (as shown in figure) then the time period of oscillations is T. The correct relations is

$T^{2} = T_{1}^{2} + T_{2}^{2}$

$T^{- 2} = T_{1}^{- 2} + T_{2}^{- 2}$

$T^{- 1} = T_{1}^{- 1} + T_{2}^{- 1}$

$T = T_{1} + T_{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

(b) $T = 2 π \sqrt{\frac{m}{k}} or T \propto \frac{1}{\sqrt{k}} or k = \frac{α}{T^{2}}$
Now , $k_{e} = k_{1} + k_{2}$
$∴ \frac{α}{T^{2}} = \frac{α}{T_{1}^{2}} + \frac{α}{T_{2}^{2}}$
or $T^{- 2} = T_{1}^{- 2} + T_{2}^{- 2}$

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Similar Questions

A body of mass $m$ is suspended from three springs as shown in figure. If mass $m$ is displaced slightly then time period of oscillation is

View Solution
Period of small oscillations in the two cases shown in figure is $T_{1}$ and $T_{2}$ respectively . Assume fluid does not have any viscosity , then

View Solution
A mass is suspended separately by two different springs in successive order then time period is $t_{1}$ and $t_{2}$ respectively. If it is connected by both spring as shown in figure then time period is $t_{0}$ , the correct relation is : -

View Solution
A mass m is suspended from the two coupled springs connected in series. The force constant for springs are $k_{1}$ and $k_{2} .$ The time period of the suspended mass will be
View Solution
An object suspended from a spring exhibits oscillations of period T. Now the spring is cut in two halves and the same object is suspended with two halves as shown in figure. The new time period of oscillation will become

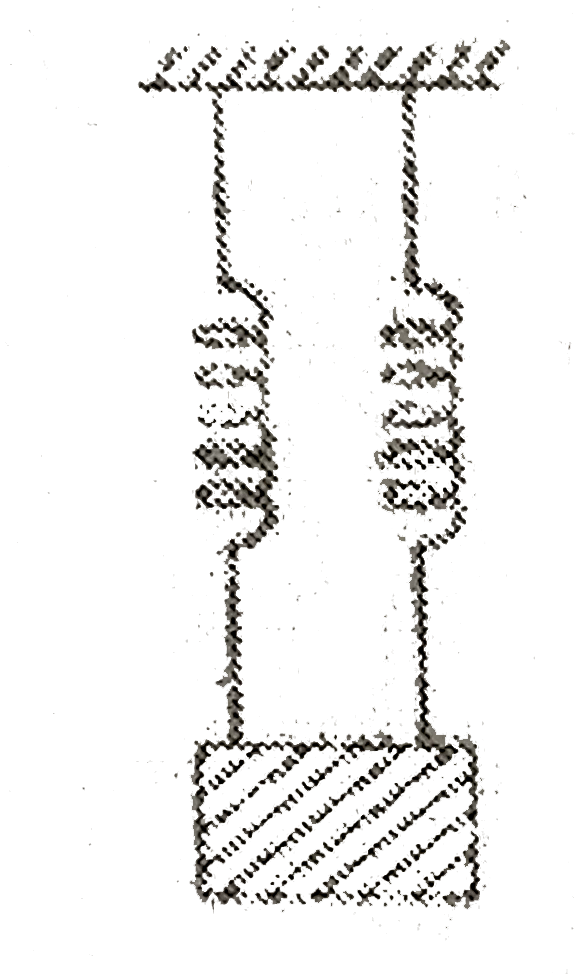
View Solution
A bar of mass $m$ is suspended horizontally on two vertical springs of spring constant $k$ and $3 k$ . The bar bounces up and down while remaining horizontal. Find the time period of oscillation of the bar neglect mass of springs and friction everywhere

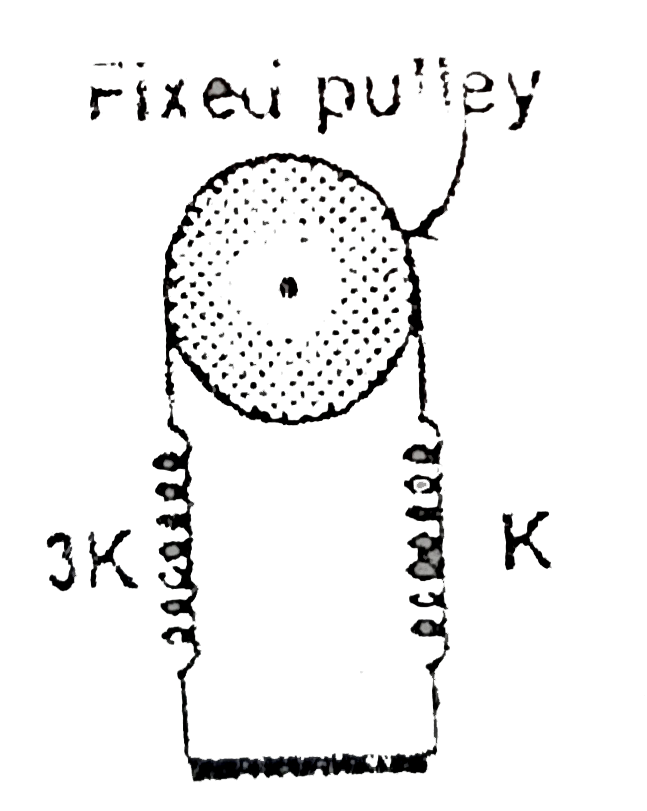
View Solution
A mass is suspended separately by two springs and the time periods in the two cases are $T_{1}$ and $T_{2}$ . Now the same mass is connected in parallel $(K = K_{1} + K_{2})$ with the springs and the time is suppose $T_{P}$ . Similarly time period in series is $T_{S}$ , then find the relation between $T_{1}, T_{2}$ and $T_{P}$ in the first case and $T_{1}, T_{2}$ and $T_{S}$ in the second case.
View Solution
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View Solution
Two springs of force constants $k_{1}$ and $k_{2}$ , are connected to a mass m as shown. The frequency of oscillation of the mass is $f$ . If both $k_{1}$ and $k_{2}$ are made four times their original values, the frequency of oscillation becomes

View Solution
Three arrangements of spring - mass system are shown in figures (A), (B) and ( C). If $T_{1}$ , $T_{2}$ and $T_{3}$ represent the respective periods of oscillation, then correct relation is

View Solution

The correct Answer is:B

(b) T=2π√mk or T∝1√k or k=αT2 Now , ke=k1+k2 ∴αT2=αT21+αT22 or T−2=T−21+T−22

Similar Questions

Recommended Questions

(b) $T = 2 π \sqrt{\frac{m}{k}} or T \propto \frac{1}{\sqrt{k}} or k = \frac{α}{T^{2}}$
Now , $k_{e} = k_{1} + k_{2}$
$∴ \frac{α}{T^{2}} = \frac{α}{T_{1}^{2}} + \frac{α}{T_{2}^{2}}$
or $T^{- 2} = T_{1}^{- 2} + T_{2}^{- 2}$