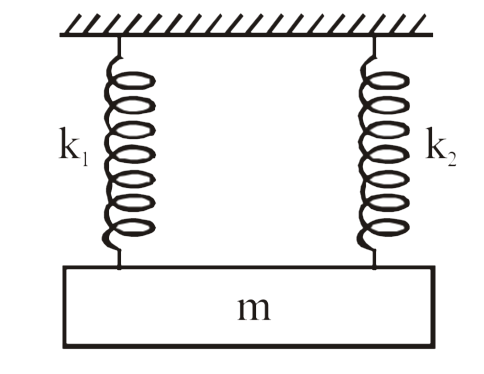
A mass is suspended separately by two springs and the time periods in the two cases are $T_{1}$ and $T_{2}$ . Now the same mass is connected in parallel $(K = K_{1} + K_{2})$ with the springs and the time is suppose $T_{P}$ . Similarly time period in series is $T_{S}$ , then find the relation between $T_{1}, T_{2}$ and $T_{P}$ in the first case and $T_{1}, T_{2}$ and $T_{S}$ in the second case.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B

$T = 2 π \sqrt{\frac{m}{K}}$
$∴ T = \frac{α}{\sqrt{K}}$
(where, $2 π \sqrt{m} = α$ = constant)
$\Rightarrow K = \frac{α^{2}}{T^{2}}$ ...(i)
or $\frac{1}{K} = \frac{T^{2}}{α^{2}}$
First case In parallel,
$K = K_{1} + K_{2}$
Using Eq. (i), $\frac{α^{2}}{T_{p}^{2}} = \frac{α^{2}}{T_{1}^{2}} + \frac{α^{2}}{T^{2}}$
$∴ T_{p}^{- 2} = T_{1}^{- 2} + T_{2}^{- 2}$
This is the desired relation.
Second case In series, $\frac{1}{K} = \frac{1}{K_{1}} + \frac{1}{K_{2}}$
Now, using Eq. (ii) we have, $\frac{T_{s}^{2}}{α^{2}} = \frac{T_{1}^{2}}{α^{2}} + \frac{T_{2}^{2}}{α^{2}}$
$∴ T_{s}^{2} = T_{1}^{2} + T_{2}^{2}$
This is the desired relation in this case.

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
When a block of mass m is suspended separately by two different springs have time period $t_{1} and t_{2}$ . If same mass is connected to parallel combination of both springs, then its time period is given by :-
A $\frac{t_{1} t_{2}}{t_{1} + t_{2}}$
B $\frac{t_{1} t_{2}}{\sqrt{t_{1}^{2} + t_{2}^{2}}}$
C $\sqrt{\frac{t_{1} t_{2}}{t_{1} + t_{2}}}$
D $t_{1} + t_{2}$
Question 2 - Select One
A mass is suspended separately by two different springs in successive order then time periods is $t_{1}$ and $t_{2}$ respectively. If it is connected by both spring as shown in figure then time period is to, the correct relation is

A $t_{0}^{2} = t_{1}^{2} + t_{2}^{2}$
B $t_{0}^{- 2} = t_{1}^{- 2} + t_{2}^{- 2}$
C $t_{0}^{- 1} = t_{1}^{- 1} + t_{2}^{- 1}$
D $t_{0} = t_{1} + t_{2}$
Question 3 - Select One
A mass $m$ is suspended separately by two different springs of spring constant $k_{1}$ and $k_{2}$ given the time period $t_{1}$ and $t_{2}$ respectively. If the same mass $m$ is shown in the figure then time period $t$ is given by the relation

A $t = t_{1} + t_{2}$
B $t = \frac{t_{1} t_{2}}{t_{1} + t_{2}}$
C $t^{2} = t_{1}^{2} + t_{2}^{2}$
D $t^{- 2} = t_{1}^{- 2} + t_{2}^{- 2}$

DC PANDEY-SIMPLE HARMONIC MOTION-Example Type 5

Home
Ask Doubt
Profile