A mass is suspended separately by two springs and the time periods in the two cases are and . Now the same mass is connected in parallel with the springs and the time is suppose . Similarly time period in series is , then find the relation between and in the first case and and in the second case.
The correct Answer is:A, B
To solve the problem, we need to find the relationships between the time periods T1,T2 (for the individual springs) and TP (for the parallel connection) as well as TS (for the series connection).
1. Understanding the Time Period Formula:
The time period T of a mass-spring system is given by the formula:
T=2π√mk
where m is the mass and k is the spring constant.
2. Expressing Spring Constants in Terms of Time Periods:
Rearranging the formula, we can express the spring constant k in terms of the time period T:
k=4π2mT2
For each spring, we can write:
- For spring 1: k1=4π2mT21
- For spring 2: k2=4π2mT22
3. Finding the Equivalent Spring Constant for Parallel Connection:
When the two springs are connected in parallel, the equivalent spring constant KP is given by:
KP=k1+k2
Substituting the expressions for k1 and k2:
KP=4π2mT21+4π2mT22
This can be simplified to:
KP=4π2m(1T21+1T22)
4. Relating TP to T1 and T2:
The time period TP for the parallel connection can be expressed as:
TP=2π√mKP
Substituting for KP:
TP=2π
⎷m4π2m(1T21+1T22)
Simplifying this gives:
TP=2π
⎷14π2(1T21+1T22)
TP=1√1T21+1T22
Thus, we have:
T−2P=T−21+T−22
5. Finding the Equivalent Spring Constant for Series Connection:
When the springs are connected in series, the equivalent spring constant KS is given by:
1KS=1k1+1k2
Substituting:
1KS=T214π2m+T224π2m
This simplifies to:
1KS=T21+T224π2m
6. Relating TS to T1 and T2:
The time period TS for the series connection can be expressed as:
TS=2π√mKS
Substituting for KS:
TS=2π√m⋅4π2mT21+T22
This gives:
T2S=4π2mKS
Thus, we have:
T2S=T21+T22
Final Relations:
- For parallel connection:
T−2P=T−21+T−22
- For series connection:
T2S=T21+T22
The time period T of a mass-spring system is given by the formula:
T=2π√mk
where m is the mass and k is the spring constant.
Rearranging the formula, we can express the spring constant k in terms of the time period T:
k=4π2mT2
For each spring, we can write:
- For spring 1: k1=4π2mT21
- For spring 2: k2=4π2mT22
When the two springs are connected in parallel, the equivalent spring constant KP is given by:
KP=k1+k2
Substituting the expressions for k1 and k2:
KP=4π2mT21+4π2mT22
This can be simplified to:
KP=4π2m(1T21+1T22)
The time period TP for the parallel connection can be expressed as:
TP=2π√mKP
Substituting for KP:
TP=2π
⎷m4π2m(1T21+1T22)
Simplifying this gives:
TP=2π
⎷14π2(1T21+1T22)
TP=1√1T21+1T22
Thus, we have:
T−2P=T−21+T−22
When the springs are connected in series, the equivalent spring constant KS is given by:
1KS=1k1+1k2
Substituting:
1KS=T214π2m+T224π2m
This simplifies to:
1KS=T21+T224π2m
The time period TS for the series connection can be expressed as:
TS=2π√mKS
Substituting for KS:
TS=2π√m⋅4π2mT21+T22
This gives:
T2S=4π2mKS
Thus, we have:
T2S=T21+T22
- For parallel connection:
T−2P=T−21+T−22
- For series connection:
T2S=T21+T22
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Example Type 6
Explore 4 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Example Type 7
Explore 1 Video
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Example Type 4
Explore 1 Video
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEY ENGLISHChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
When a block of mass m is suspended separately by two different springs have time period t1 and t2. If same mass is connected to parallel combination of both springs, then its time period is given by :-
View SolutionA mass is suspended separately by two springs of spring constants k1 and k2 in successive order. The time periods of oscillations in the two cases are T1 and T2 respectively. If the same mass be suspended by connecting the two springs in parallel, (as shown in figure) then the time period of oscillations is T. The correct relations is

View Solution
Knowledge Check
When a body is suspended from two light springs separately, the periods of vertical oscillations are T1 and T2. When the same body is suspended from the two spring connected in series, the period will be
AT=T1+T2B1T=1T1+1T2CT2=T21+T22D1T2=1T21+1T2
A mass is suspended separately by two different springs in successive order then time period is t1 and t2 respectively. If it is connected by both spring as shown in figure then time period is t0, the correct relation is : -

View SolutionA projectile has same range for two angules of projection. If times of flight in two cases are t1andt2 then the range of the projectilie is
View SolutionA body of mass m has time period T1 with one spring and has time period T2 with another spring. If both the springs are connected in parallel and same mass is used, then new time period T is given as
View SolutionTwo springs are made to oscillate simple harmonically due to the same mass individually. The time periods obtained are T1 and T2. If both the springs are connected in series and then made to oscillate by the same mass, the resulting time period will be
View SolutionIf 'P' is in equilibrium then T1/T2 is
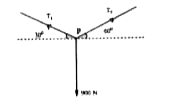
View SolutionLet T1 and T2 be the time periods of two springs A and B when a mass m is suspended from them separately. Now both the springs are connected in parallel and same mass m is suspended with them. Now let T be the time period in this position. Then
View SolutionPeriod of small oscillations in the two cases shown in figure is T1 and T2 respectively . Assume fluid does not have any viscosity , then

View Solution