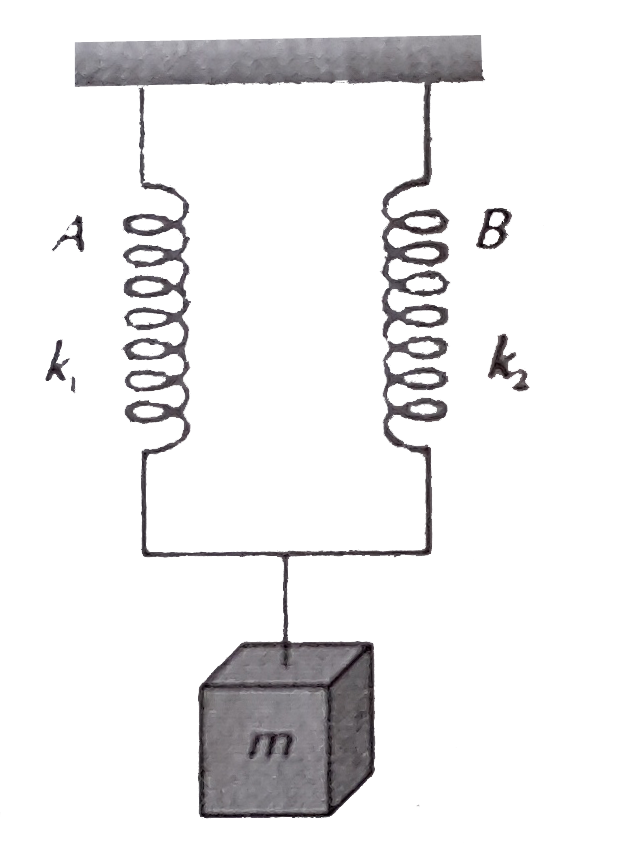
A mass m is suspended from the two coupled springs connected in series. The force constant for springs are k1andk2. The time period of the suspended mass will be
T=2π√(mk1+k2)
T=2π√(mk1+k2)
T=2pisqrt((((m)(k_(1)+k_(2)))/(k_(1)k_(2))))
T=2pisqrt(((mk_(1)k_(2))/(k_(1)+k_(2))))
Step by step video & image solution for A mass m is suspended from the two coupled springs connected in series. The force constant for springs are k_(1) "and" k_(2). The time period of the suspended mass will be by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two springs are joined and attached to a mass of 16 kg. The system is then suspended vertically from a rigid support. The spring constant of the two springs are K1 and K2 respectively. The period of vertical oscillations of the system will be:
View SolutionWhen a body is suspended from two light springs separately, the periods of vertical oscillations are T1 and T2. When the same body is suspended from the two spring connected in series, the period will be
View Solution
Knowledge Check
A mass m is suspended from the two coupled springs connected in series. The force constant for spring are k1 and k2. The time period of the suspended mass will be:
AT=2π√mk1−k2BT=2π√mk1k2k1+k2CT=2π√mk1+k2DT=2π√m(k1+k2)k1k2A mass m is suspended by means of two coiled springs which have the same length in unstretched condition as shown in figure. Their force constants are k1andk2 respectively. When set into vertical vibrations, the period will be
 A2π√(mk1k2)B2π√m(k1k2)C2π√(mk1−k2)D2π√(mk1+k2)
A2π√(mk1k2)B2π√m(k1k2)C2π√(mk1−k2)D2π√(mk1+k2)A mass m is suspended separately by two different springs of spring constant k1 and k2 given the time period t1 and t2 respectively. If the same mass m is shown in the figure then time period t is given by the relation
 At=t1+t2Bt=t1t2t1+t2Ct2=t21+t22Dt−2=t−21+t−22
At=t1+t2Bt=t1t2t1+t2Ct2=t21+t22Dt−2=t−21+t−22
A mass m is suspended by means of two coiled spring which have the same length in unstretched condition as in figure. Their force constant are k 1 and k 2 respectively. When set into vertical vibrations, the period will be
View SolutionWhen a body is suspended from two light springs separately, the periods of vertical oscillations are T1 and T2. When the same body is suspended from the two spring connected in series, the period will be
View SolutionA mass is suspended separately by two springs of spring constants k1 and k2 in successive order. The time periods of oscillations in the two cases are T1 and T2 respectively. If the same mass be suspended by connecting the two springs in parallel, (as shown in figure) then the time period of oscillations is T. The correct relations is

View SolutionTwo springs are joined and attached to a mass of 16 kg. The system is then suspended vertically from a rigid support. The spring constant of the two spring are k1andk2 respectively. The period of vertical oscillations of the system will be
View SolutionLet T1 and T2 be the time periods of two springs A and B when a mass m is suspended from them separately. Now both the springs are connected in parallel and same mass m is suspended with them. Now let T be the time period in this position. Then
View Solution

