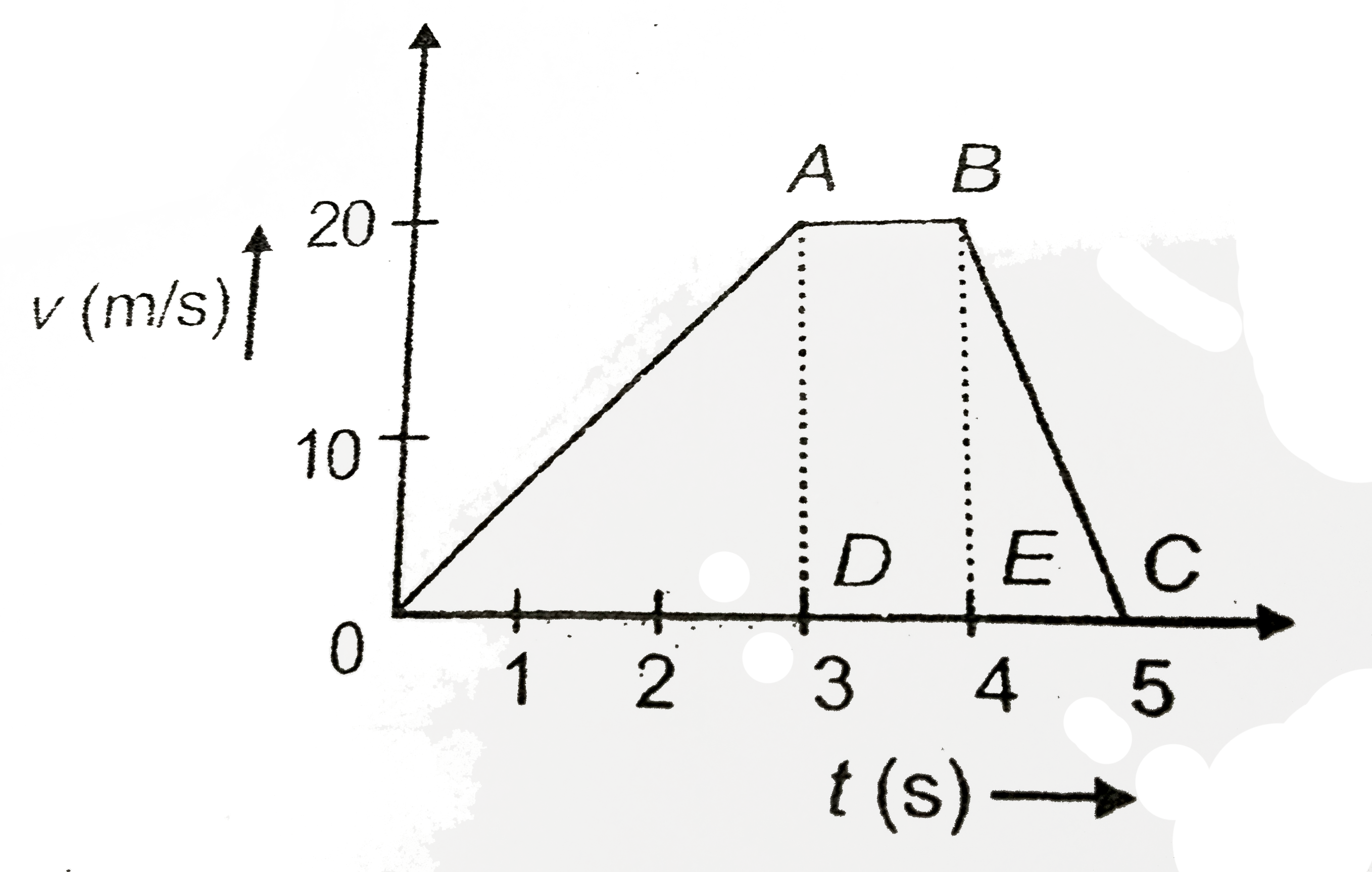
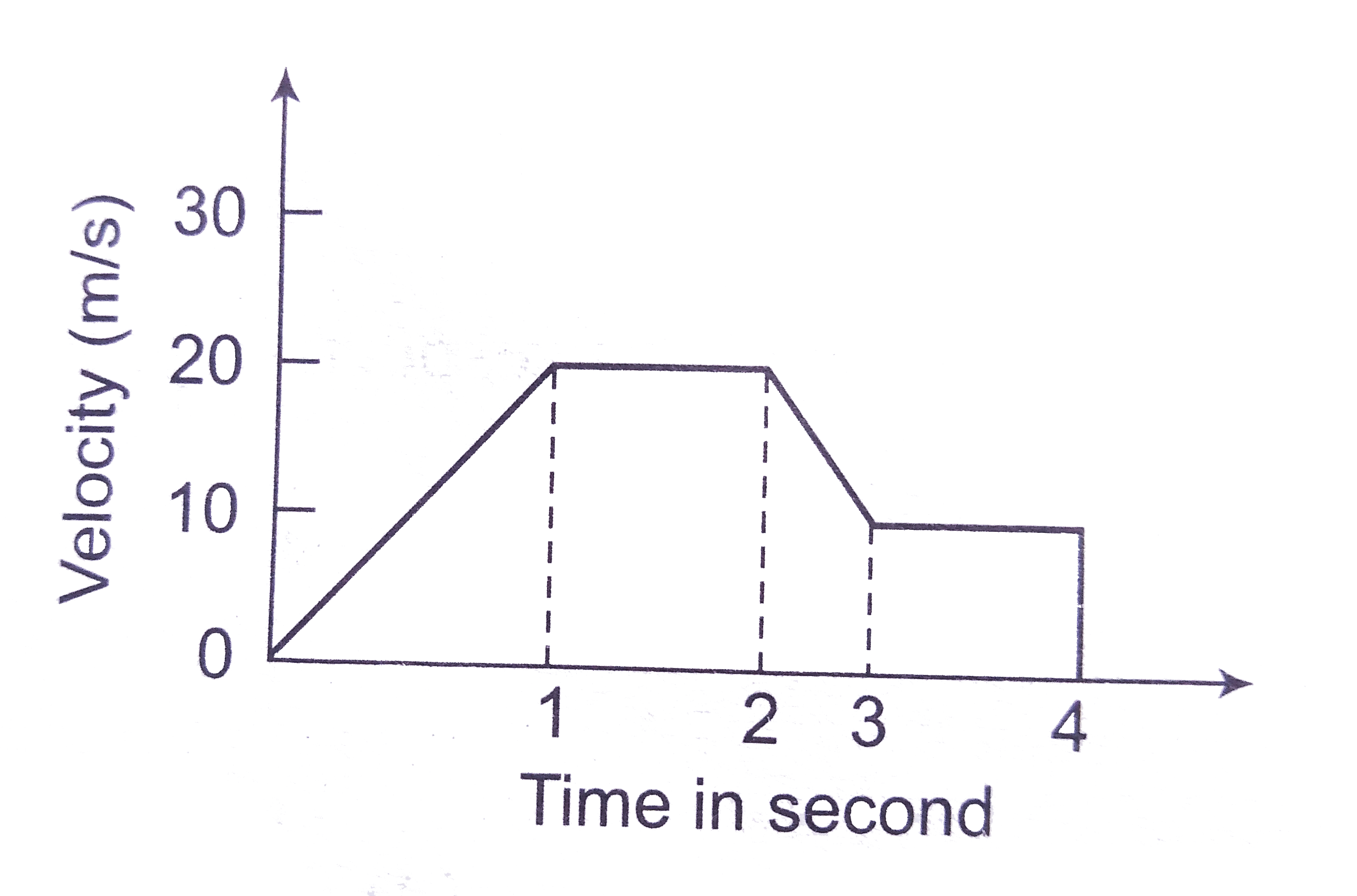
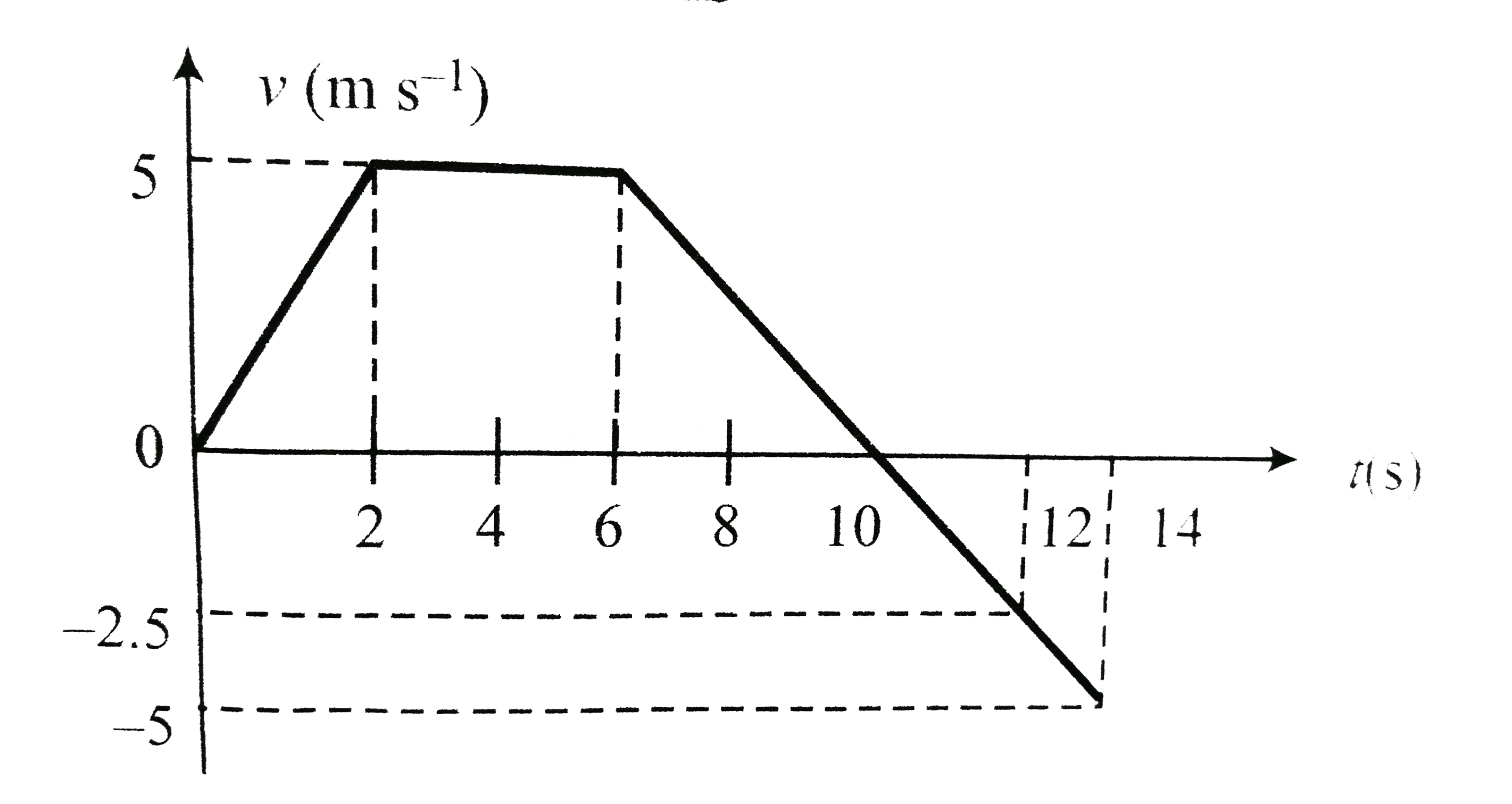
The variation of velocity of a particle with time moving along a straight line is illustrated in the following figure. The distance travelled by the particle in four seconds is.
60 m
55 m
25 m
30 m
The correct Answer is:B
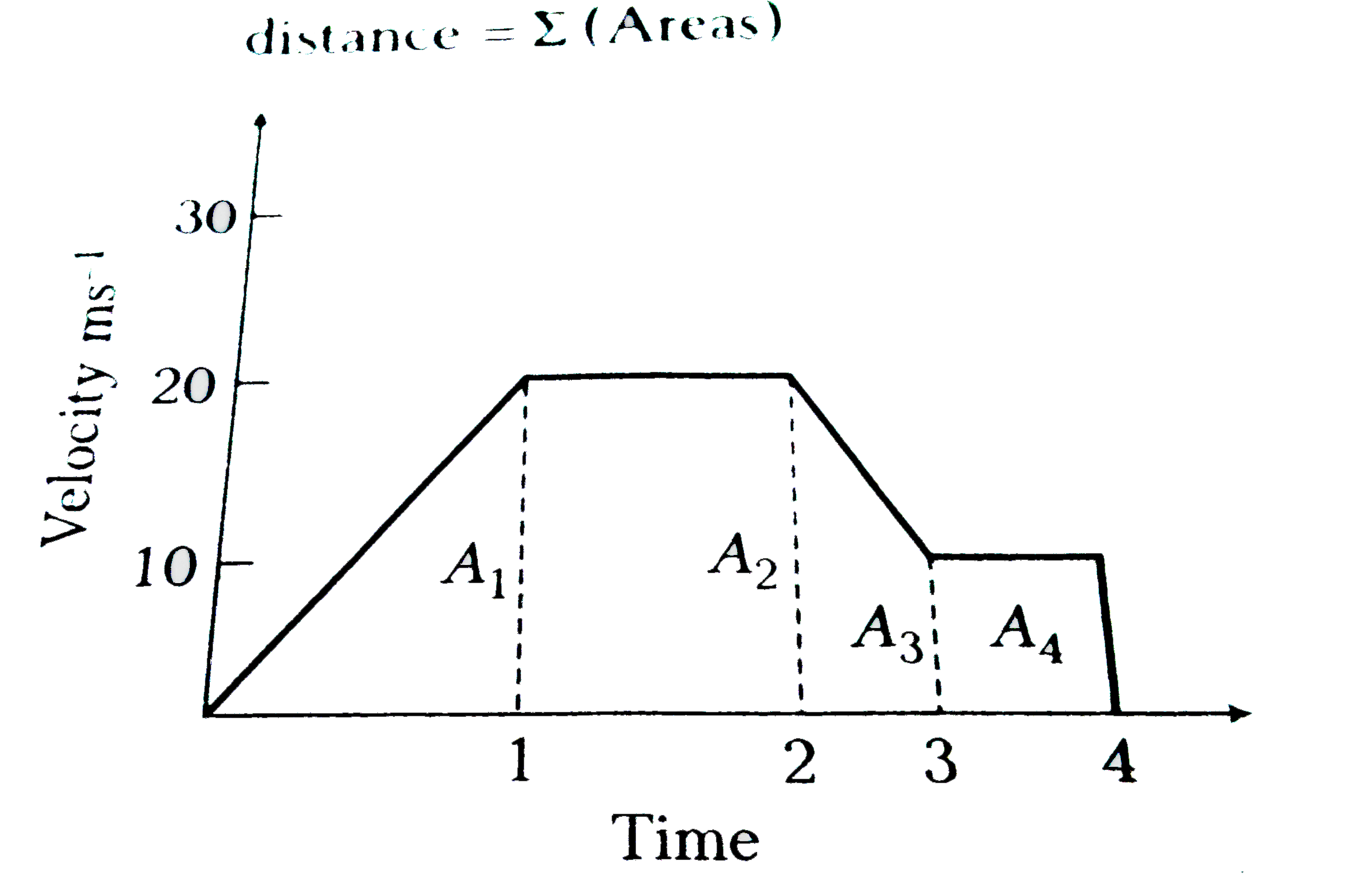
Distance = Area under graph =
Displacement = positive area - negative area
Topper's Solved these Questions
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:Check point 3.7
Explore 15 Videos
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:(A) Taking it together
Explore 75 Videos
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:Check point 3.5
Explore 25 Videos
- MOTIONBook:DC PANDEY ENGLISHChapter:MOTIONExercise:Medical entrances gallery
Explore 19 Videos
- PROJECTILE MOTIONBook:DC PANDEY ENGLISHChapter:PROJECTILE MOTIONExercise:Level - 2 Subjective
Explore 10 Videos
Similar Questions
Knowledge Check
The variataion of velocity of a particle moving along a straight line is illustrated in the following Fig. 3.1. The distance traversed by the particle in 4 seconds is
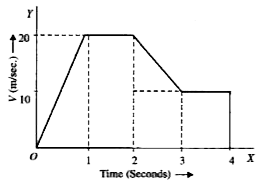 A60 mB25 mC55 mD30 m
A60 mB25 mC55 mD30 m
The variation of velocity of a particle moving along a straight line is shown in the figure. The distance travelled by the particle in 4s is
View SolutionVelocity of a particle moving along a straight line at any time 't' is give by V=cos(π3t) . Then the distance travelled by the particle in the first two seconds is :
View SolutionIf a particle is moving along straight line with increasing speed, then
View SolutionThe velocity time plot for a particle moving on straight line is shown in the figure.

View SolutionThe velocity time plot for a particle moving on straight line is shown in the figure.

View SolutionVariation of displacement x of a particle moving on a straight line with time t is shown in following figure. The figure indicates :

View SolutionVariation of displacement x of a particle moving on a straight line with time t is shown in following figure. The figure indicates :

View Solution
 .
.