Let IAandIB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of massof the body but B does not. Choose the correct option.
IA<IB
IA<IB, whether the axes are parallel or not parallel
if the axes are parallel IA<IB
If the axes are not parallel IA≥IB
The correct Answer is:C
To solve the problem regarding the moments of inertia IA and IB of a body about two axes A and B, we will use the concept of the Parallel Axis Theorem.
1. Identify the Axes:
- Axis A passes through the center of mass (CM) of the body.
- Axis B is parallel to axis A but does not pass through the center of mass.
2. Recall the Parallel Axis Theorem:
The Parallel Axis Theorem states that the moment of inertia about any axis (B) can be calculated using the moment of inertia about the center of mass (A) plus the product of the mass of the body (m) and the square of the distance (d) between the two axes:
IB=ICM+m⋅d2
3. Substituting Values:
Since axis A passes through the center of mass, we can denote:
ICM=IA
Therefore, we can rewrite the equation for IB:
IB=IA+m⋅d2
4. Analyze the Relationship:
Since m⋅d2 is a positive quantity (as mass and distance squared are always positive), we can conclude that:
IB=IA+m⋅d2>IA
This implies that:
IB>IA
5. Choose the Correct Option:
Based on our analysis, the correct option is that the moment of inertia about axis B is greater than the moment of inertia about axis A:
- Thus, the correct statement is: IB>IA.
Conclusion:
The answer to the question is that the moment of inertia about axis B is greater than that about axis A, which corresponds to option three.
- Axis A passes through the center of mass (CM) of the body.
- Axis B is parallel to axis A but does not pass through the center of mass.
The Parallel Axis Theorem states that the moment of inertia about any axis (B) can be calculated using the moment of inertia about the center of mass (A) plus the product of the mass of the body (m) and the square of the distance (d) between the two axes:
IB=ICM+m⋅d2
Since axis A passes through the center of mass, we can denote:
ICM=IA
Therefore, we can rewrite the equation for IB:
IB=IA+m⋅d2
Since m⋅d2 is a positive quantity (as mass and distance squared are always positive), we can conclude that:
IB=IA+m⋅d2>IA
This implies that:
IB>IA
Based on our analysis, the correct option is that the moment of inertia about axis B is greater than the moment of inertia about axis A:
- Thus, the correct statement is: IB>IA.
The answer to the question is that the moment of inertia about axis B is greater than that about axis A, which corresponds to option three.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises
25 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
Let IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not. Then
View SolutionThe moment of inertia of a body about a given axis of rotation depends upon :-
View Solutionfind moment of inertia about an axis yy which passes through the centre of mass of the two particle system as shown
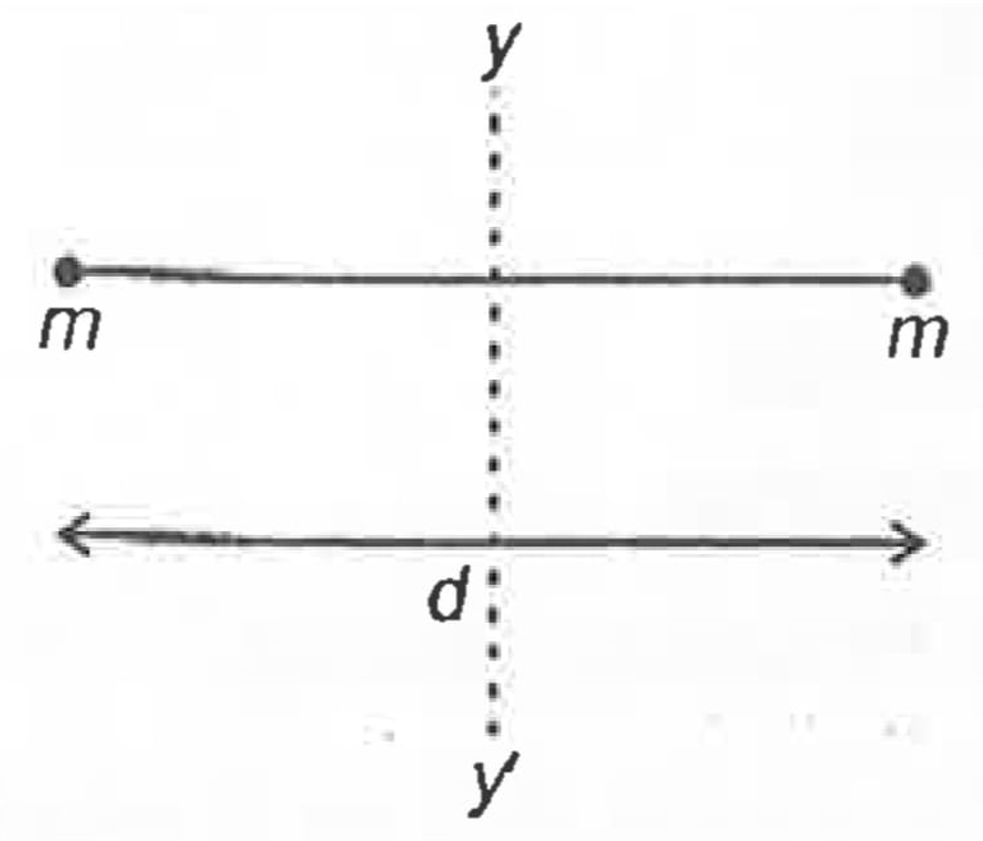
View SolutionThe moment of inertia of a hollow cubical box of mass M and side a about an axis passing through the centres of two opposite faces is equal to.
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
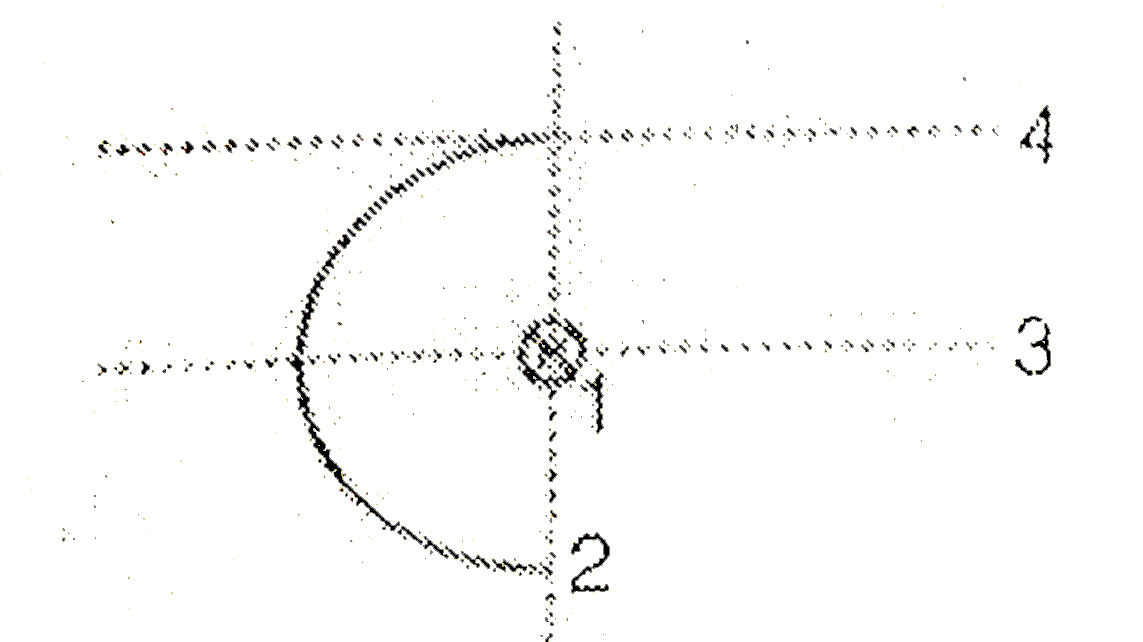
View SolutionA semi-circular ring has mass m and radius R as shown in figure. Let I1,I2,I3 and I4 be the moments of inertia about the four axes as shown . Axis 1 passes through centre and is perpendicular to plane of ring. Then , match the following.

View SolutionConsider a uniform square plate shown in the figure. I1,I2, I3 and I4 are moment of inertia of the plate about the axes 1, 2, 3 and 4 respectively. Axes 1 and 2 are diagonals and 3 and 4 are lines passing through centre parallel to sides of the square. The moment of inertia of the plate about an axis passing through centre and perpendicular to the plane of the figure is equal to which of the followings.
A. I3 + I4
B. I1 + I3
C. I2 + I3
D. 12 (I1+I2+I3+I4)
View SolutionIf I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 is the moment of inertia of the ring about an axis perpendicular to plane of ring and passing through its centre formed by bending the rod, then
View Solution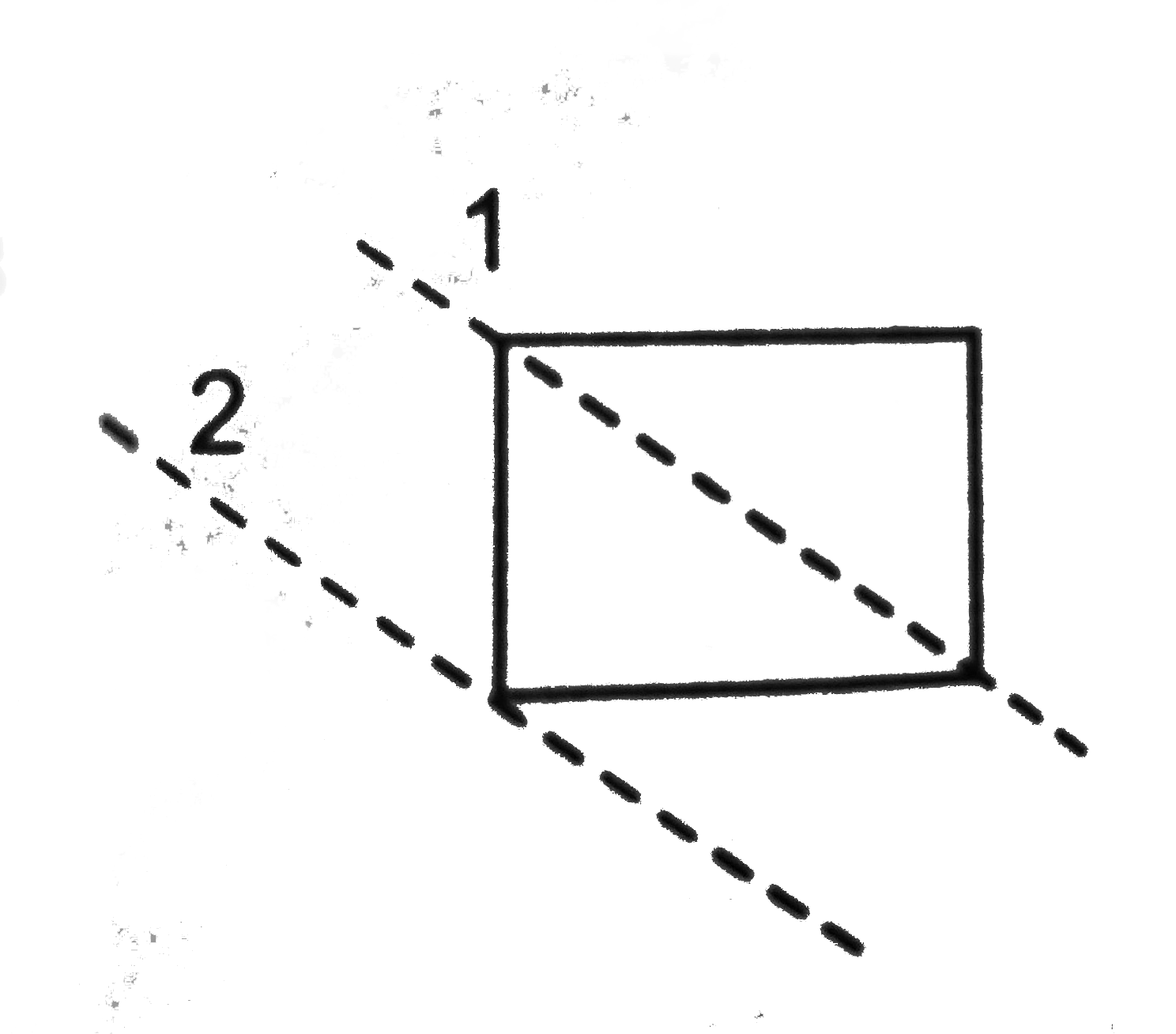
Let I1 and I2 be the moment of inertia of a uniform square plate about axes shown in the figure. Then the ratio I1:I2 is
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View Solution
