A rigid body rotates with an angular momentum L. If its rotational kinetic energy is made 4 times, its angular momentum will become
4L
16L
√2L
2L
The correct Answer is:D
To solve the problem, we need to understand the relationship between angular momentum (L) and rotational kinetic energy (K) of a rigid body.
1. Understand the Definitions:
- The angular momentum (L) of a rigid body is given by the formula:
L=Iω
where I is the moment of inertia and ω is the angular velocity.
- The rotational kinetic energy (K) is given by:
K=12Iω2
2. Relate Angular Momentum and Rotational Kinetic Energy:
- We can express K in terms of L:
K=12Iω2=12L2I
- From this, we can derive that:
L2=2KI
- Thus, we can express L in terms of K:
L=√2KI
3. Determine the Effect of Increasing Kinetic Energy:
- If the rotational kinetic energy is made 4 times, we denote the new kinetic energy as K′=4K.
- Substituting this into our expression for angular momentum:
L′=√2K′I=√2(4K)I=√8KI=2√2KI
- Since L=√2KI, we can rewrite L′ as:
L′=2L
4. Conclusion:
- Therefore, if the rotational kinetic energy is made 4 times, the new angular momentum L′ becomes:
L′=2L
Final Answer:
The angular momentum will become 2L.
- The angular momentum (L) of a rigid body is given by the formula:
L=Iω
where I is the moment of inertia and ω is the angular velocity.
- The rotational kinetic energy (K) is given by:
K=12Iω2
- We can express K in terms of L:
K=12Iω2=12L2I
- From this, we can derive that:
L2=2KI
- Thus, we can express L in terms of K:
L=√2KI
- If the rotational kinetic energy is made 4 times, we denote the new kinetic energy as K′=4K.
- Substituting this into our expression for angular momentum:
L′=√2K′I=√2(4K)I=√8KI=2√2KI
- Since L=√2KI, we can rewrite L′ as:
L′=2L
- Therefore, if the rotational kinetic energy is made 4 times, the new angular momentum L′ becomes:
L′=2L
The angular momentum will become 2L.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises
25 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
A particle moving in a circular path has an angular momentum of L. If the frequency of rotation is halved, then its angular momentum becomes
View SolutionOnly rotating bodies can have angular momentum.
View SolutionDefine angular momentum. What is its physical significance ?
View SolutionA particle attached to a string is rotating with a constant angular velocity and its angular momentum is L. If the string is halved and angular velocity is kept constant, the angular momentum will be
View SolutionA particle performing uniform circular motion gas angular momentum L. If its angular frequency is double and its kinetic energy halved, then the new angular momentum is :
View SolutionA particle performing uniform circular motion has angular momentum L. If its angular frequency is double and its kinetic energy halved, then the new angular momentum is :
View SolutionA ring of diameter 1m is rotating with an angular momentum of 10 Joule-sec. The necessary tangential force required to increase its angular momentum by 50 % in 1 sec will be (in newtons)
View SolutionThe rotational kinetic energy of a body is E and its moment of inertia is I. The angular momentum is
View SolutionA uniform circular disc of mass 200 g and radius 4.0 cm is rotated about one of its diameter at an angular speed of 10 rad/s. Find the kinetic energy of the disc and its angular momentum about the axis of rotation.
View SolutionTwo cylinders having radii 2R and R and moment of inertia 4I and I about their central axes are supported by axles perpendicular to their planes. The large cylinder is initially rotating clockwise with angular velocity ω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually slipping ceases and the two cylinders rotate at constant rates in opposite directions. During this
(A) angular momentum of system is conserved
(B) kinetic energy is conserved
(C neither the angular momentum nor the kinetic energy is conserved
(D) both the angular momentum and kinetic energy are conserved
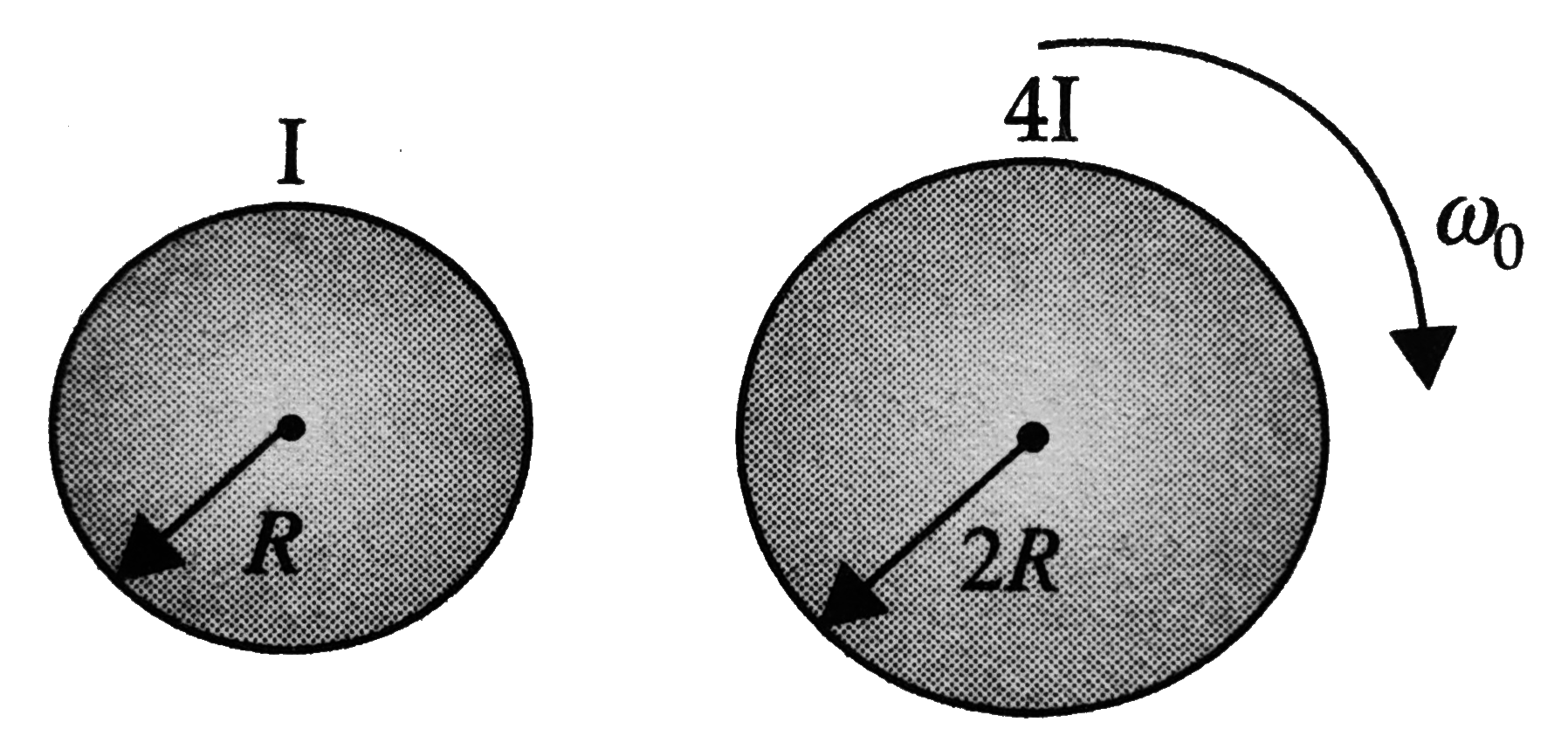
View Solution
