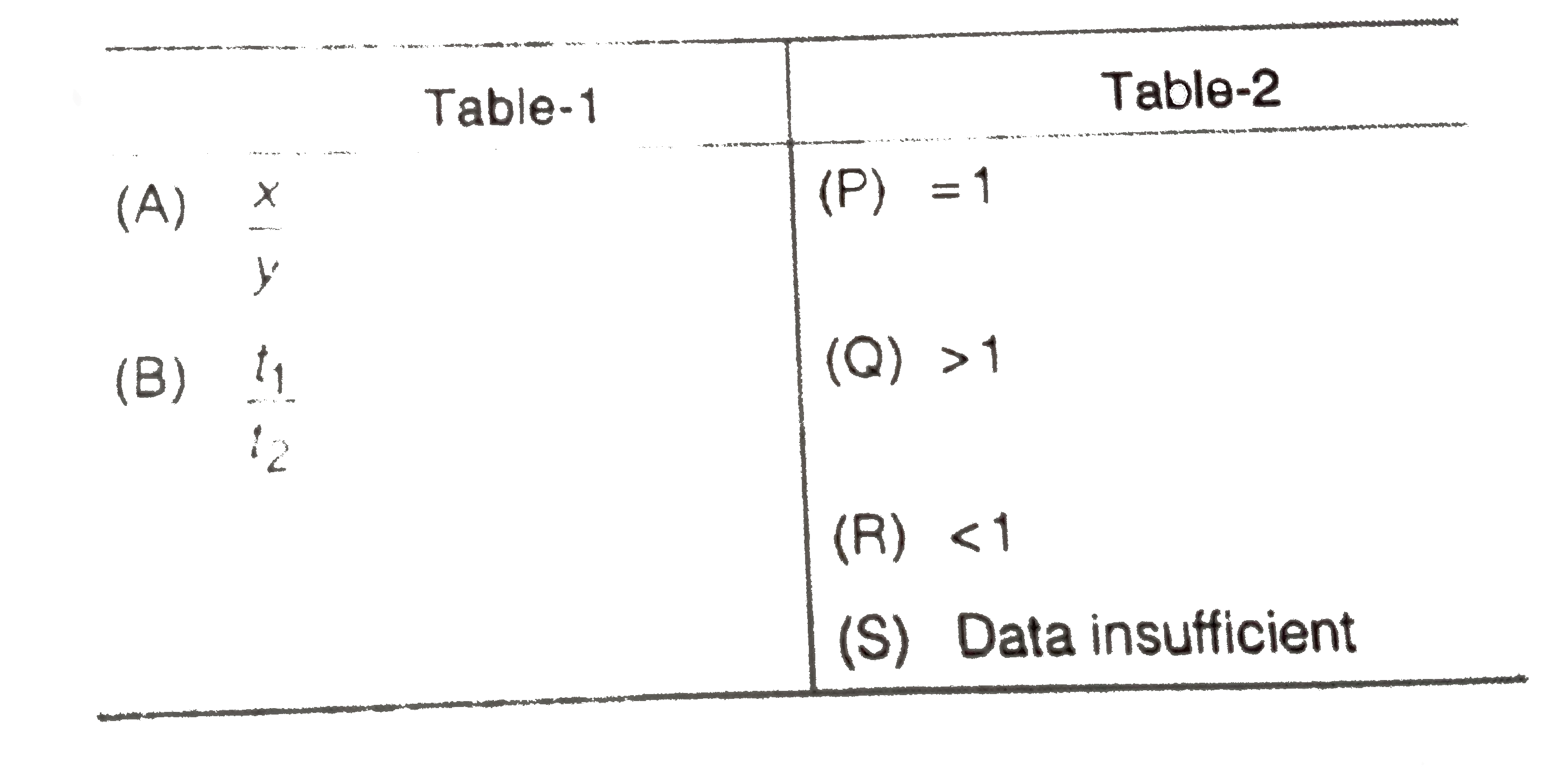
A particle is projected from the surface of earth with speed v. Suppose it travel a distance x when its speed become v to $\frac{v}{2}$ and y when speed changes form $\frac{v}{2}$ to 0. Similarly, the corresponding times are suppose $t_{1} and t_{2}$ . Then

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $(A \to q, B \to p)$

Given, $g = \frac{G M}{R^{2}} = constant (∵ x < < R and Y < < R)$
When speed become $v$ to $\frac{v}{2}$
$(\frac{v}{2}) = v - g \times t_{1} \Rightarrow t_{1} = \frac{v}{2 g}$
and ${(\frac{v}{2})}^{2} = v^{2} - 2 g x \Rightarrow \frac{3 v^{2}}{8 g}$
Similarly, $0 = \frac{v}{2} - g \times t_{2} \Rightarrow t_{2} = \frac{v}{2 g}$
and $0 = {(\frac{v}{2})}^{2} - 2 g y \Rightarrow y = \frac{v^{2}}{8 g}$
Clearly $t_{1} = t_{2}, x > y$ .

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A vehicle travels half the distance (L) with speed $V_{1}$ and the other half with speed $V_{2}$ , then its average speed is .
Aa. $v_{1} + \frac{v_{2}}{2}$
Bb. $2 v_{1} + \frac{v_{2}}{v_{1}} + v_{2}$
Cc. $2 v_{1} \frac{v_{2}}{v_{1} + v_{2}}$
Dd. $\frac{v_{1} + v_{2}}{v_{1}} v_{2}$
Question 2 - Select One
A particle is thrown with a speed is at an angle $θ$ with the horizontal. When the particle makes an angle $ϕ$ with the horizontal, its speed changes to v, then
A $v = v_{0} cos θ$
B $v = v_{0} cos θ \cdot cos ϕ$
C $v = v_{0} cos θ \cdot sec ϕ$
D $v = v_{0} sec θ \cdot cos ϕ$

DC PANDEY ENGLISH-GRAVITATION-(B) Chapter Exercises

Home
Ask Doubt
Profile