Assertion : Let W1 be the work done in taking away a satellite from the surface of earth to its orbit and then W2 the work done in rotating the satellite in circular orbit there. Then, W1=W2
Reason : W2=GMm4R
If both Assertin and Reason are correct and Reason is the correct explanation of Assertion
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion
If Assertion is true but Reason is false
If Assertion is false but Reason is true
The correct Answer is:D
To solve the problem, we need to analyze both the assertion and the reason provided.
1. Understanding the Assertion:
- The assertion states that the work done in moving a satellite from the surface of the Earth to its orbit (W₁) is equal to the work done in rotating the satellite in its circular orbit (W₂).
2. Calculating W₁ (Work Done to Move the Satellite):
- When moving a satellite from the Earth's surface to a height h, the work done can be calculated using the formula:
W1=mgh
- However, since the gravitational force changes with height, we need to integrate the force over the distance. The work done against gravity when moving to a height h is:
W1=∫R+hRGMmr2dr
- Evaluating this integral gives:
W1=GMm(1R−1R+h)=GMmhR(R+h)
3. Calculating W₂ (Work Done to Rotate the Satellite):
- The work done to keep the satellite in circular motion at height h is related to its kinetic energy. The gravitational force provides the necessary centripetal force for circular motion.
- The speed v of the satellite in orbit is given by:
v=√GMR+h
- The kinetic energy (which is also the work done to maintain the satellite in orbit) is:
W2=12mv2=12m(GMR+h)=GMm2(R+h)
4. Comparing W₁ and W₂:
- From our calculations, we have:
W1=GMmhR(R+h)
W2=GMm2(R+h)
- For W1 to equal W2, we would need:
GMmhR(R+h)=GMm2(R+h)
- This equality does not hold true in general, indicating that the assertion W1=W2 is false.
5. Evaluating the Reason:
- The reason states that W2=GMm4R. This is incorrect based on our calculation of W2, which is GMm2(R+h).
Conclusion:
- The assertion is false, and the reason is also false. Therefore, the statement "if assertion is false but reason is true" is incorrect.
- The assertion states that the work done in moving a satellite from the surface of the Earth to its orbit (W₁) is equal to the work done in rotating the satellite in its circular orbit (W₂).
- When moving a satellite from the Earth's surface to a height h, the work done can be calculated using the formula:
W1=mgh
- However, since the gravitational force changes with height, we need to integrate the force over the distance. The work done against gravity when moving to a height h is:
W1=∫R+hRGMmr2dr
- Evaluating this integral gives:
W1=GMm(1R−1R+h)=GMmhR(R+h)
- The work done to keep the satellite in circular motion at height h is related to its kinetic energy. The gravitational force provides the necessary centripetal force for circular motion.
- The speed v of the satellite in orbit is given by:
v=√GMR+h
- The kinetic energy (which is also the work done to maintain the satellite in orbit) is:
W2=12mv2=12m(GMR+h)=GMm2(R+h)
- From our calculations, we have:
W1=GMmhR(R+h)
W2=GMm2(R+h)
- For W1 to equal W2, we would need:
GMmhR(R+h)=GMm2(R+h)
- This equality does not hold true in general, indicating that the assertion W1=W2 is false.
- The reason states that W2=GMm4R. This is incorrect based on our calculation of W2, which is GMm2(R+h).
- The assertion is false, and the reason is also false. Therefore, the statement "if assertion is false but reason is true" is incorrect.
Topper's Solved these Questions
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:(C) Chapter Exercises
Explore 45 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:(A) Chapter Exercises
Explore 68 Videos
- GENERAL PHYSICSBook:DC PANDEY ENGLISHChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 10 Videos
Similar Questions
The work done in taking a unit positive charge from P to A is WA and P to B is WB. Then
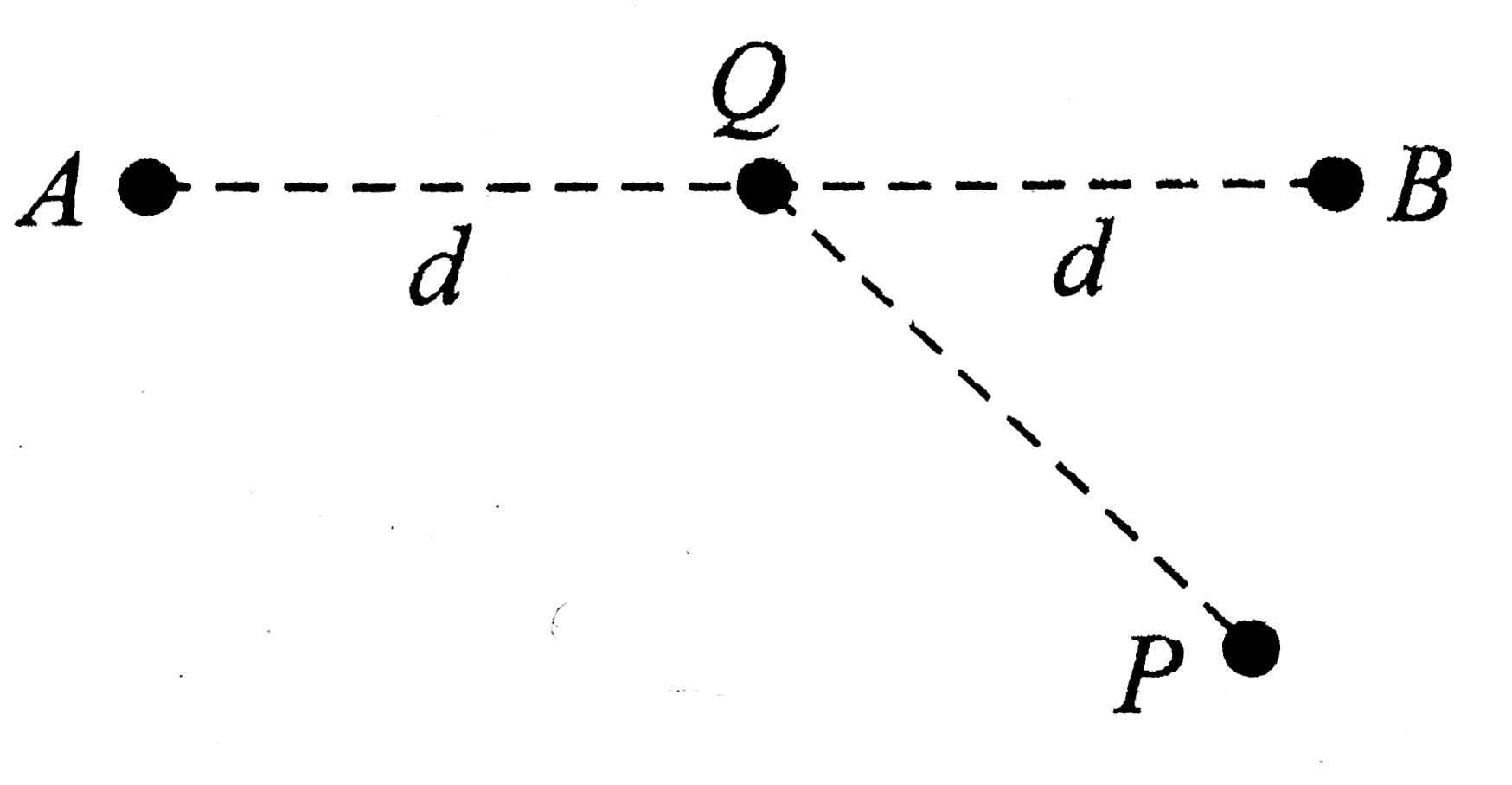 .
.
View SolutionA satellite revolves around a planet in a circular orbit. What is the work done by the satellite at any instant ? Give a reason.
View SolutionWork done in forming a liquid drop of radius R is W1 and that of radius 3R is W2. The ratio of work done is
View SolutionA satellite of earth of mass 'm' is taken from orbital radius 2R to 3R, then minimum work done is :-
View SolutionWhen the work is done by the system, w is taken as ......
View SolutionThe work done in blowing a bubble of radius R is W. What is the work done in making a bubble of radius 2R? Given both the bubble are to be made with the same solution.
View Solutionif work is done by the system then W is
View SolutionIf WABC is the work done in process A→B→C and WDEF is work done in process D→E→F as shown in the figure, then

View SolutionIf W1W2 and W3 represent the work done in moving a particle from A to B along three different paths 1.2 and3 respectively (asshown ) in the gravitational fieled of a point mass m, find the correct relation between W_(1) W_(2)andW_(3)
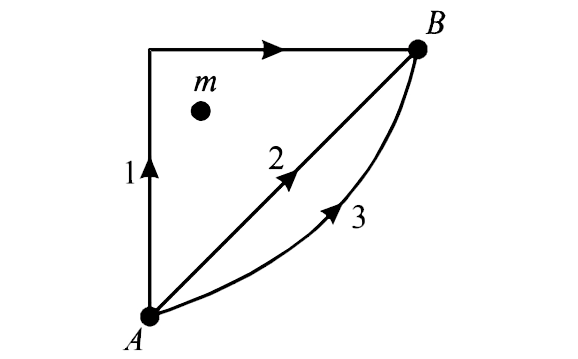
View SolutionIf W1W2 and W3 represent the work done in moving a particle from A to B along three different paths 1.2 and3 respectively (asshown ) in the gravitational fieled of a point mass m, find the correct relation between W_(1) W_(2)andW_(3)

View Solution