Work done in forming a liquid drop of radius R is W1 and that of radius 3R is W2. The ratio of work done is
The correct Answer is:10
To find the ratio of work done in forming a liquid drop of radius R (denoted as W1) and that of radius 3R (denoted as W2), we can follow these steps:
Step 1: Understand the Concept of Surface Energy
The work done in forming a liquid drop is related to the change in surface energy. The surface energy of a liquid drop is given by the formula:
Surface Energy=Surface Tension×Surface Area
Thus, the work done W in forming a drop is equal to the surface energy of that drop.
Step 2: Calculate the Surface Area for Each Drop
The surface area A of a sphere (which is the shape of a drop) is given by:
A=4πr2
For a drop of radius R:
A1=4πR2
For a drop of radius 3R:
A2=4π(3R)2=4π×9R2=36πR2
Step 3: Calculate the Work Done for Each Drop
Using the surface tension T, we can express the work done in forming each drop:
- For the drop of radius R:
W1=T×A1=T×4πR2
- For the drop of radius 3R:
W2=T×A2=T×36πR2
Step 4: Find the Ratio of Work Done
Now we can find the ratio of the work done:
W1W2=T×4πR2T×36πR2
The T, 4π, and R2 terms cancel out:
W1W2=436=19
Conclusion
Thus, the ratio of work done in forming a liquid drop of radius R to that of radius 3R is:
W1:W2=1:9
The work done in forming a liquid drop is related to the change in surface energy. The surface energy of a liquid drop is given by the formula:
Surface Energy=Surface Tension×Surface Area
Thus, the work done W in forming a drop is equal to the surface energy of that drop.
The surface area A of a sphere (which is the shape of a drop) is given by:
A=4πr2
For a drop of radius R:
A1=4πR2
For a drop of radius 3R:
A2=4π(3R)2=4π×9R2=36πR2
Using the surface tension T, we can express the work done in forming each drop:
- For the drop of radius R:
W1=T×A1=T×4πR2
- For the drop of radius 3R:
W2=T×A2=T×36πR2
Now we can find the ratio of the work done:
W1W2=T×4πR2T×36πR2
The T, 4π, and R2 terms cancel out:
W1W2=436=19
Thus, the ratio of work done in forming a liquid drop of radius R to that of radius 3R is:
W1:W2=1:9
Topper's Solved these Questions
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL -2
50 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE MAIN (LEVEL - 1 )
31 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL-0 ( Short Answer Type - II )
15 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
Similar Questions
The work done to split a liquid drop id radius R into N identical drops is (taken σ as the surface tension of the liquid)
View SolutionIn order to shift a body of mass m from a circular orbit of radius 3R to a higher orbit of radius 5R around the earth, the work done is
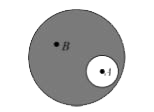
View SolutionThere is an air bubble of radius R inside a drop of water of radius 3R. Find the ratio of gauge pressure at point B to that at point A.
View SolutionA spherical liquid drop of radius R is divided into eight equal droplets. If the surface tension is T, then the work done in this process will be
View SolutionThe work done in blowing a bubble of radius R is W. What is the work done in making a bubble of radius 2R? Given both the bubble are to be made with the same solution.
View SolutionThe work done in blowing a bubble of radius R is W. What is the work done in making a bubble of radius 2R? Given both the bubble are to be made with the same solution.
View SolutionAssertion : Let W1 be the work done in taking away a satellite from the surface of earth to its orbit and then W2 the work done in rotating the satellite in circular orbit there. Then, W1=W2
Reason : W2=GMm4R
View SolutionA satellite of earth of mass 'm' is taken from orbital radius 2R to 3R, then minimum work done is :-
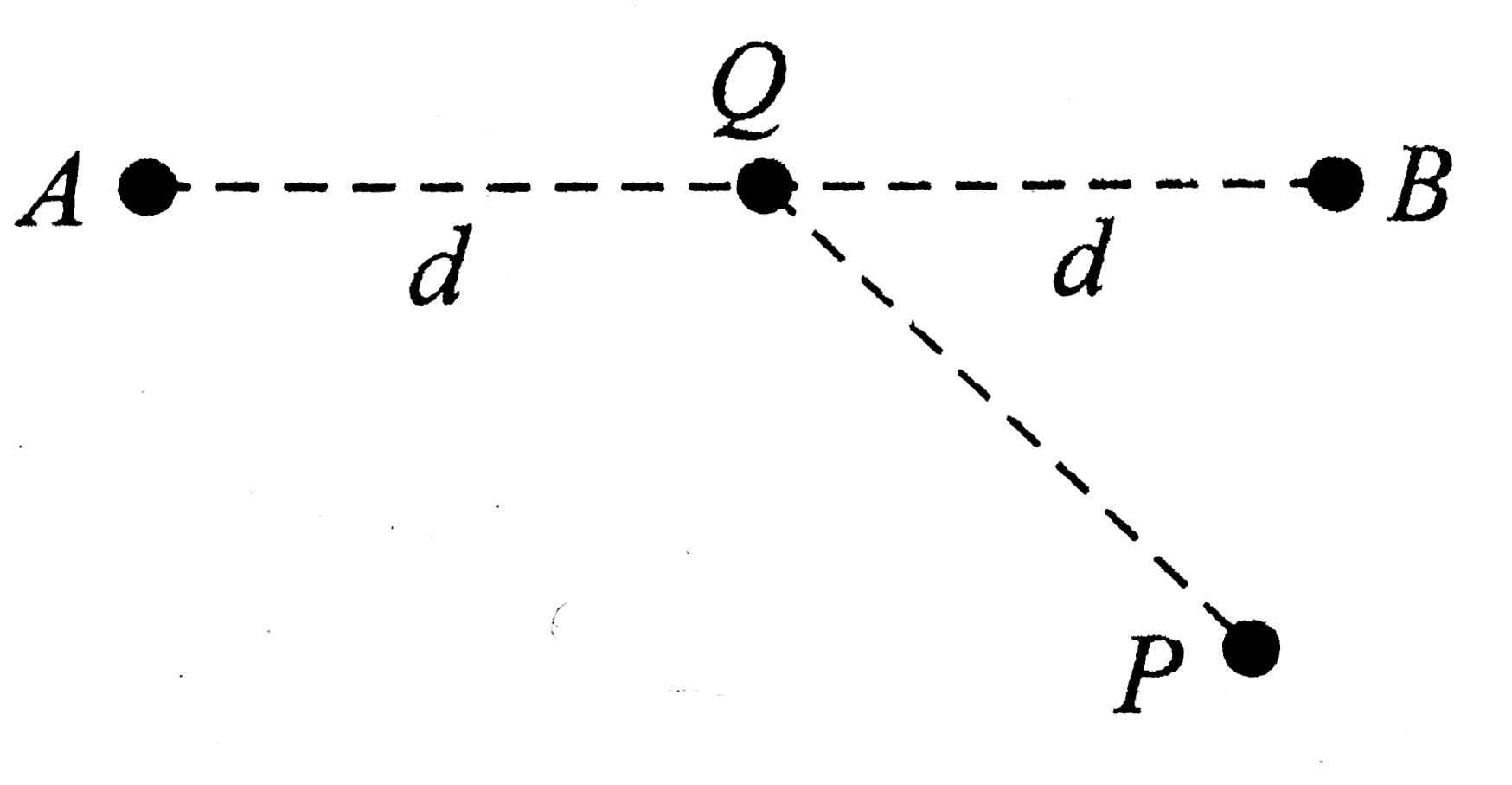
View SolutionThe work done in taking a unit positive charge from P to A is WA and P to B is WB. Then
 .
.
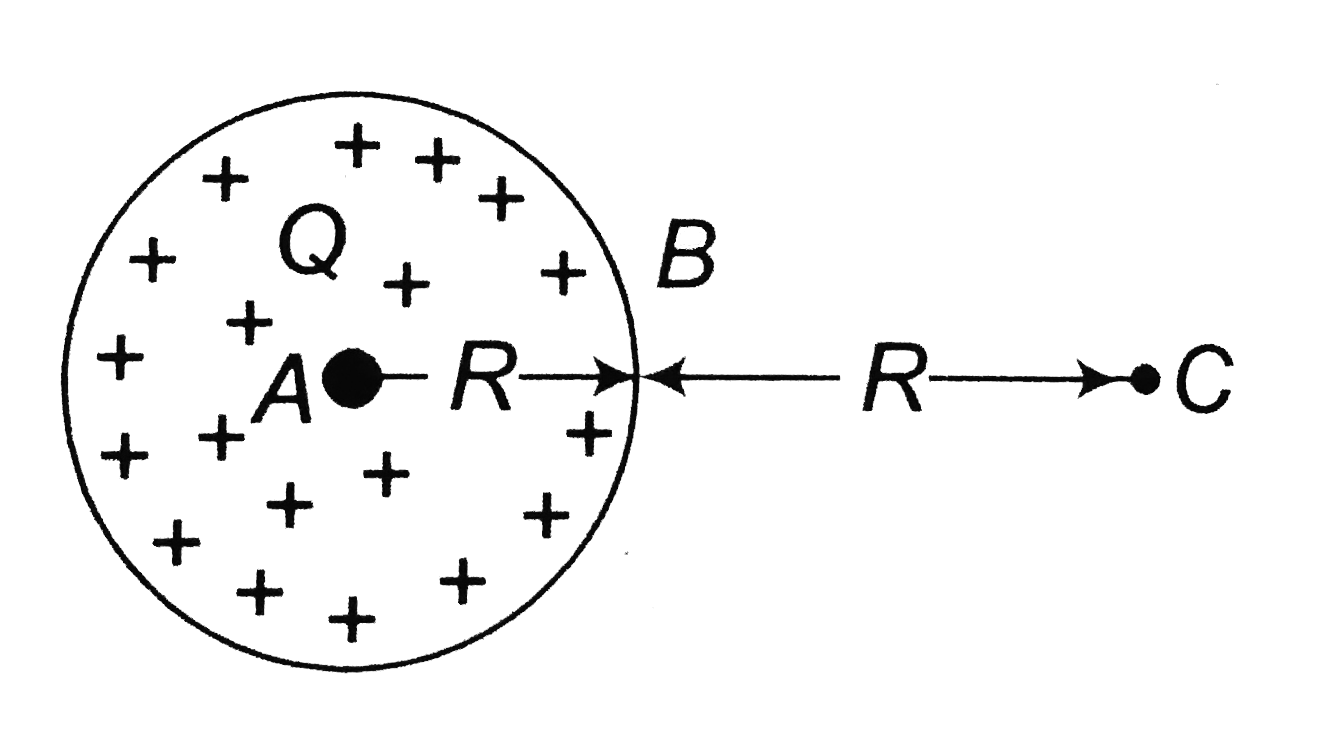
View SolutionFind the ratio of electric work done in bringing a charge q from A to B(WAB) and that from B to C(WBC) in a sphere of charge Q distributed uniformly throughout its volume.
View Solution
