On the surface of earth acceleration due gravity is g and gravitational potential is V. Match of following columns
Column-IColumn-II(A)At height h=R, value of g(p)Decreases by a factor14(B)At depth h=R2,value of g(q)Decrease by a factor12(C)At height h=R,value of V(r)Increase by a factor118(D)At height h=R2,value of V(s)Increase by a factor 2(t)None
The correct Answer is:(A→q,B→q,C→q,D→t)
To solve the problem, we need to analyze the changes in the acceleration due to gravity (g) and gravitational potential (V) at different heights and depths relative to the Earth's surface.
1. At height h=R:
- The formula for acceleration due to gravity at height h is:
gh=g(1+hR)2
- Substituting h=R:
gh=g(1+1)2=g4
- Thus, the value of g decreases by a factor of 14.
- Match: (A) with (p).
2. At depth h=R2:
- The formula for acceleration due to gravity at depth d is:
gd=g(1−dR)
- Substituting d=R2:
gd=g(1−12)=g2
- Thus, the value of g decreases by a factor of 12.
- Match: (B) with (q).
3. At height h=R for gravitational potential V:
- The formula for gravitational potential at height h is:
Vh=−GMR+h
- Substituting h=R:
Vh=−GMR+R=−GM2R
- The potential at the surface is V=−GMR. The ratio of the potentials is:
VhV=−GM2R−GMR=12
- Thus, the potential decreases by a factor of 12.
- Match: (C) with (r).
4. At height h=R2 for gravitational potential V:
- Substituting h=R2:
Vh=−GMR+R2=−GM3R2=−2GM3R
- The ratio of the potentials is:
VhV=−2GM3R−GMR=23
- Since there is no option that matches this ratio, we conclude:
- Match: (D) with (t) (None).
Final Matches:
- (A) - (p)
- (B) - (q)
- (C) - (r)
- (D) - (t)
- The formula for acceleration due to gravity at height h is:
gh=g(1+hR)2
- Substituting h=R:
gh=g(1+1)2=g4
- Thus, the value of g decreases by a factor of 14.
- Match: (A) with (p).
- The formula for acceleration due to gravity at depth d is:
gd=g(1−dR)
- Substituting d=R2:
gd=g(1−12)=g2
- Thus, the value of g decreases by a factor of 12.
- Match: (B) with (q).
- The formula for gravitational potential at height h is:
Vh=−GMR+h
- Substituting h=R:
Vh=−GMR+R=−GM2R
- The potential at the surface is V=−GMR. The ratio of the potentials is:
VhV=−GM2R−GMR=12
- Thus, the potential decreases by a factor of 12.
- Match: (C) with (r).
- Substituting h=R2:
Vh=−GMR+R2=−GM3R2=−2GM3R
- The ratio of the potentials is:
VhV=−2GM3R−GMR=23
- Since there is no option that matches this ratio, we conclude:
- Match: (D) with (t) (None).
- (A) - (p)
- (B) - (q)
- (C) - (r)
- (D) - (t)
Topper's Solved these Questions
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:(C) Chapter Exercises
Explore 45 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:(A) Chapter Exercises
Explore 68 Videos
- GENERAL PHYSICSBook:DC PANDEY ENGLISHChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 10 Videos
Similar Questions
If earth decreases its rotational speed. Match the following columns
Column-IColumn-II(A)Value of g at pole(p)Will remain same(B)Value of g at equator(q)Will increase(C)Distance of geostationary(r)Will decrease(D)Energy of geostationary satellite(s)Cannot say
View SolutionMatch the following columns. (for a satellite in circular orbit)
Column-IColumn-II(A)Kinetic energy(p)−GMm2r(B)Potential energy(q)√GMr(C)Total energy(r)−GMmr(D)Orbital speed(s)GMm2r
View SolutionMatch the following
Column-IColumn-II(A)Enthalpy(p)Extensive property(B)Entropy(q)H - TS(C)Free energy(r)E + PV(D)Pressure(s)Intensive property
View SolutionMatch the following columns.
∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣Column IColumn II(A)d v/dt(p)Acceleration(B)d|v|/dt(q)Magnitude of acceleration(C)drdt(r)Velocity(D)∣∣drdt∣∣(s)Magnitude of velocity(t)Rate of change of speed∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionMatch the following :
Column -IColumn -II(A)Acceleration due to gravity(p)Kepler's law(B)Law of periods(q)Vector quantity(C)Orbital speed(r)Uniform near earth surface(D)Gravitational potential(s)Is nearly zero at infinity
View SolutionThe value of acceleration due to gravity will be 1% of its value at the surface of earth at a height of (Re=6400km)
View SolutionIn the diagram shown in figure mass of both the balls in same. Match the following columns.
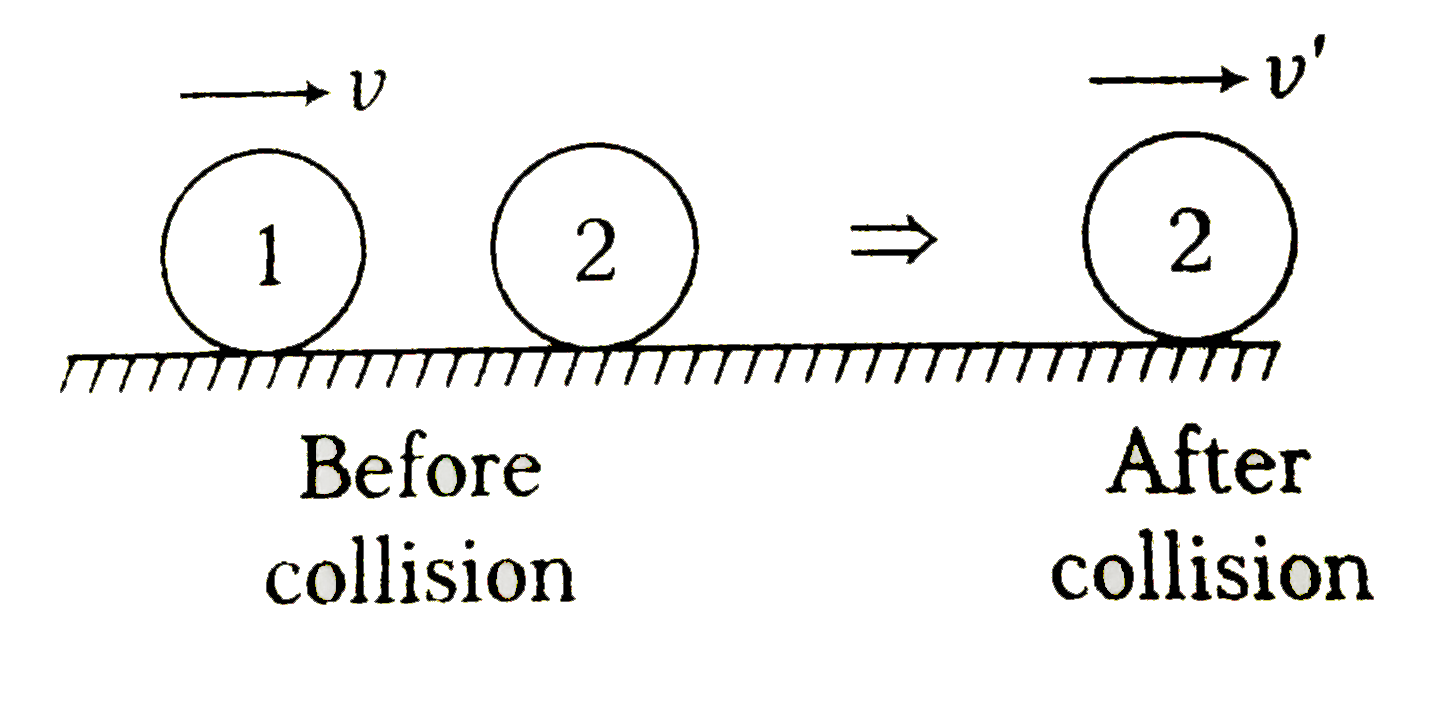
Column1Column2A Forv′=vP e=0B Forv′=v/2Q e=1C Forv′=3/4vR e=1/2-(S data is insufficient
View SolutionMatch the following columns.
Column IColumn IIA.Teslap[ML2A−2T−2]B.Weberq[MLA−2T−1]C.Weber m−2r.[MA−1T−2]D.Henrys.None
View SolutionAt what depth below the surface of earth, value of accelaration due to gravity is same as the value at height h =R1, where R is the radius of earth.
View SolutionIf ge,gh and gd be the acceleration due to gravity at earth’s surface, a height h and at depth d respectively . Then:
View Solution

