Match the following columns
Column-IColumn-II(A)Time period of an earthsatellite in circular orbit(p)Independent of mass of satellite(B)Orbital velocity of satellite(q)Independent of radius of orbit(C)Mechanical energy of satellite(r)Independent of mass of earth(s)None
The correct Answer is:(A→p,B→p,C→s)
To solve the matching question, we need to analyze each item in Column-I and determine its relationship with the items in Column-II based on the properties of satellites in circular orbits.
1. Time period of an Earth satellite in circular orbit (A):
- The formula for the time period (T) of a satellite in circular orbit is given by:
T=2π√r3GM
where r is the radius of the orbit and M is the mass of the Earth.
- From this formula, we can see:
- Independent of mass of satellite: True, as the mass of the satellite does not appear in the formula. (Matches with (p))
- Independent of radius of orbit: False, as T is directly proportional to r3/2.
- Independent of mass of Earth: False, as T is inversely proportional to √M.
Thus, A matches with (p).
2. Orbital velocity of satellite (B):
- The formula for the orbital velocity (V) of a satellite is given by:
V=√GMr
- Analyzing this formula:
- Independent of mass of satellite: True, as the mass of the satellite does not appear in the formula. (Matches with (p))
- Independent of radius of orbit: False, as V is inversely proportional to √r.
- Independent of mass of Earth: False, as V is directly proportional to √M.
Thus, B matches with (p).
3. Mechanical energy of satellite (C):
- The mechanical energy (E) of a satellite is given by:
E=−GMm2r
where m is the mass of the satellite.
- Analyzing this:
- Independent of mass of satellite: False, as E depends on m.
- Independent of radius of orbit: False, as E is inversely proportional to r.
- Independent of mass of Earth: False, as E is directly proportional to M.
Thus, C matches with (s) (None).
Final Matching:
- A → (p)
- B → (p)
- C → (s)
Summary of Matches:
- (A) → (p)
- (B) → (p)
- (C) → (s)
- The formula for the time period (T) of a satellite in circular orbit is given by:
T=2π√r3GM
where r is the radius of the orbit and M is the mass of the Earth.
- From this formula, we can see:
- Independent of mass of satellite: True, as the mass of the satellite does not appear in the formula. (Matches with (p))
- Independent of radius of orbit: False, as T is directly proportional to r3/2.
- Independent of mass of Earth: False, as T is inversely proportional to √M.
- The formula for the orbital velocity (V) of a satellite is given by:
V=√GMr
- Analyzing this formula:
- Independent of mass of satellite: True, as the mass of the satellite does not appear in the formula. (Matches with (p))
- Independent of radius of orbit: False, as V is inversely proportional to √r.
- Independent of mass of Earth: False, as V is directly proportional to √M.
- The mechanical energy (E) of a satellite is given by:
E=−GMm2r
where m is the mass of the satellite.
- Analyzing this:
- Independent of mass of satellite: False, as E depends on m.
- Independent of radius of orbit: False, as E is inversely proportional to r.
- Independent of mass of Earth: False, as E is directly proportional to M.
- A → (p)
- B → (p)
- C → (s)
- (A) → (p)
- (B) → (p)
- (C) → (s)
Topper's Solved these Questions
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:(C) Chapter Exercises
Explore 45 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:(A) Chapter Exercises
Explore 68 Videos
- GENERAL PHYSICSBook:DC PANDEY ENGLISHChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 10 Videos
Similar Questions
Knowledge Check
The orbit of geostationary satellite is circular, the time period of satellite depeds on (i) mass of the satellite, (ii) mass of earth, (iii) radius of the orbit and (iv) height of the satellite from the surface of the earth
A(i) onlyB(i) and (ii)C(i),(ii) and (iii)D(ii),(iii) and (iv)Match the Column I with Column II
For a satellite in circular orbit
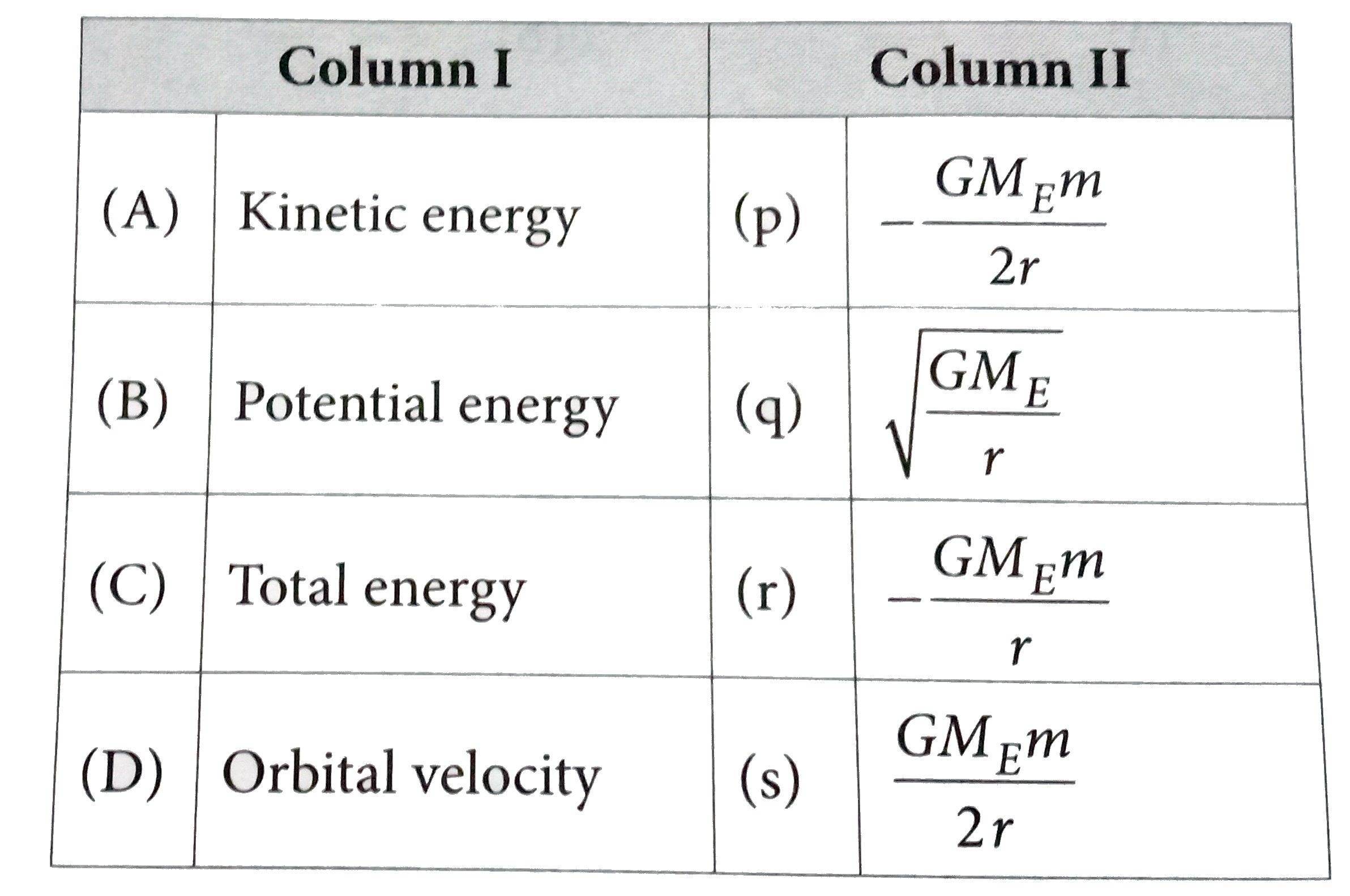
(where ME is the mass of the earth , m is the mass of the satellite and r is the radius of the orbit )AA-r, B-s,C-q,D-pBA-q,B-p,C-r,D-sCA-p,B-q,C-s,D-rDA-s,B-r,C-p,D-qA satellite is orbiting the earth in a circular orbit of radius r. Its
AKnetic enegy varies as rBangular momentum varies as 1√rClinear momentum varies as 1rDfrequency of revolution varies as 1r3/2
A satellite moves around the earth in a circular orbit with speed v. If m is the mass of the satellite, its total energy is
View SolutionTime period of a simple pendulum inside a satellite orbiting earth is
View SolutionA satellite of Sun is in a circular orbit around the Sun, midway between the Suna and earth. Find the period of this satellite.
View SolutionMatch the following columns. (for a satellite in circular orbit)
Column-IColumn-II(A)Kinetic energy(p)−GMm2r(B)Potential energy(q)√GMr(C)Total energy(r)−GMmr(D)Orbital speed(s)GMm2r
View SolutionThe period of a satellite in a circular orbit of radius R is T. What is the period of another satellite in a circular orbit of radius 4 R ?
View Solution

