An object moves from position (3,4) to (6,5) in the xy-plane. Find the magnitude and direction of displacement vector of the particle.
To find the magnitude and direction of the displacement vector of an object moving from position (3, 4) to (6, 5) in the xy-plane, we can follow these steps:
Step 1: Identify Initial and Final Positions
The initial position of the object is given as (x1,y1)=(3,4) and the final position is (x2,y2)=(6,5).
Step 2: Write Position Vectors
The initial position vector r1 can be expressed as:
r1=3^i+4^j
The final position vector r2 can be expressed as:
r2=6^i+5^j
Step 3: Calculate the Displacement Vector
The displacement vector r is calculated by subtracting the initial position vector from the final position vector:
r=r2−r1=(6^i+5^j)−(3^i+4^j)
Simplifying this gives:
r=(6−3)^i+(5−4)^j=3^i+1^j
Step 4: Find the Magnitude of the Displacement Vector
The magnitude of the displacement vector |r| can be calculated using the Pythagorean theorem:
|r|=√(3)2+(1)2=√9+1=√10
Step 5: Find the Direction of the Displacement Vector
To find the direction of the displacement vector, we calculate the angle θ with respect to the x-axis using the tangent function:
tanθ=yx=13
Thus, the angle θ is given by:
θ=tan−1(13)
Calculating this gives:
θ≈18.43∘
Final Result
The magnitude of the displacement vector is √10 and the direction is approximately 18.43∘ from the x-axis.
---
The initial position of the object is given as (x1,y1)=(3,4) and the final position is (x2,y2)=(6,5).
The initial position vector r1 can be expressed as:
r1=3^i+4^j
The final position vector r2 can be expressed as:
r2=6^i+5^j
The displacement vector r is calculated by subtracting the initial position vector from the final position vector:
r=r2−r1=(6^i+5^j)−(3^i+4^j)
Simplifying this gives:
r=(6−3)^i+(5−4)^j=3^i+1^j
The magnitude of the displacement vector |r| can be calculated using the Pythagorean theorem:
|r|=√(3)2+(1)2=√9+1=√10
To find the direction of the displacement vector, we calculate the angle θ with respect to the x-axis using the tangent function:
tanθ=yx=13
Thus, the angle θ is given by:
θ=tan−1(13)
Calculating this gives:
θ≈18.43∘
The magnitude of the displacement vector is √10 and the direction is approximately 18.43∘ from the x-axis.
Topper's Solved these Questions
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Check Point 4.1
15 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Check Point 4.2
20 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
Similar Questions
An object moves from position (6,8) to (12,10) in the x-y plane. Magnitude and direction of displacement is
View SolutionFind the magnitude and direction of the resultant of given vectors
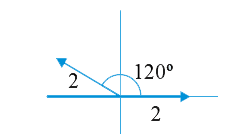
View SolutionA particle moves in xy-plane from position (1m,2m) to (3m,4m) in 2s. Find the magnitude and direction of average velocity.
View SolutionA particle moves in xy-plane from position (2m, 4m) to (6m,8m) is 2s. Magnitude and direction of average velocity is
View SolutionFind magnitude and direction cosines of the vector, A=(3ˆi−4ˆj+5ˆk).
View SolutionA particle is initially at point A(2,4,6)m moves finally to the pointB(3,2,−3)m. Write the initial position vector,final position,and displacement vector of the particle.
View SolutionA point mass 10 g moves in the xy plane with a velocity 2ms−1 along a straight line. Find the magnitude and direction of its angular momentum (i) with respect to the origin O and (ii) with respect to the origin O. The magnitude of the position vector →r is 0.5 m and the angle θ=30∘.
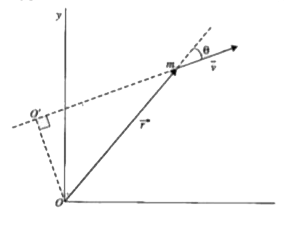
View SolutionTwo objects AandB are moving along the directions as shown in (Fig. 5.77). Find the magnitude and direction of the relative velocity of Bw.r.t.A.
 ,
,
View SolutionA particle moves along a path ABCD as shown in the figure. Then the magnitude of net displacement of the particle from position A to D is:

View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
View Solution
