For an object thrown at 45∘ to the horizontal, the maximum height H and horizontal range R are related as
R=16H
R=8H
R=4H
R=2H
The correct Answer is:C
To find the relationship between the maximum height H and the horizontal range R for an object thrown at an angle of 45∘ to the horizontal, we can follow these steps:
1. Identify the formulas for maximum height and range:
- The maximum height H for a projectile is given by the formula:
H=u20sin2θ2g
- The horizontal range R is given by the formula:
R=u20sin2θg
2. Substitute θ=45∘:
- For θ=45∘:
- sin45∘=1√2
- sin2×45∘=sin90∘=1
3. Calculate maximum height H:
- Substitute θ=45∘ into the height formula:
H=u20sin245∘2g=u20(1√2)22g=u20⋅122g=u204g
4. Calculate horizontal range R:
- Substitute θ=45∘ into the range formula:
R=u20sin90∘g=u20⋅1g=u20g
5. Relate R and H:
- Now we have:
H=u204gandR=u20g
- To find the relationship between R and H, we can take the ratio:
RH=u20gu204g=u20g⋅4gu20=4
- Therefore, we can conclude:
R=4H
Final Result:
The relationship between the horizontal range R and the maximum height H for an object thrown at an angle of 45∘ is:
R=4H
- The maximum height H for a projectile is given by the formula:
H=u20sin2θ2g
- The horizontal range R is given by the formula:
R=u20sin2θg
- For θ=45∘:
- sin45∘=1√2
- sin2×45∘=sin90∘=1
- Substitute θ=45∘ into the height formula:
H=u20sin245∘2g=u20(1√2)22g=u20⋅122g=u204g
- Substitute θ=45∘ into the range formula:
R=u20sin90∘g=u20⋅1g=u20g
- Now we have:
H=u204gandR=u20g
- To find the relationship between R and H, we can take the ratio:
RH=u20gu204g=u20g⋅4gu20=4
- Therefore, we can conclude:
R=4H
The relationship between the horizontal range R and the maximum height H for an object thrown at an angle of 45∘ is:
R=4H
Topper's Solved these Questions
- MOTIONBook:DC PANDEY ENGLISHChapter:MOTIONExercise:C. Medical entrances gallery
Explore 1 Video
- MEASUREMENT AND ERRORSBook:DC PANDEY ENGLISHChapter:MEASUREMENT AND ERRORSExercise:Subjective
Explore 19 Videos
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:(C )Medical entrances gallery
Explore 32 Videos
Similar Questions
An object is projected at an angle of 45∘ with the horizontal. The horizontal range and the maximum height reached will be in the ratio.
View SolutionA stone projected with a velocity u at an angle (theta )with the horizontal reaches maximum heights H1. When it is projected with velocity u at an angle (π2−θ) with the horizontal, it reaches maximum height H2. The relations between the horizontal range R of the projectile, H1andH2, is
View Solution
Knowledge Check
An object is thrown along a direction inclined at an angle of 45∘ with the horizontal direction. The horizontal range of the object is equal to
Avertical heightBtwice the verticalCthrice the vertical heightDfour times the vertical heightIf a body 'A' of mass M is thrown with velocity V at an angle of 30∘ to the horizontal and another body B of the same mass is thrown with the same speed at an angle of 60∘ to the horizontal, the ratio of horizontal ranges of A to B will be
A1:3B1:1C1:√3D√3:1
An object is thrown along a direction inclined at an angle of 45∘ with the horizontal direction. The horizontal range of the particle is equal to
View SolutionA body is projected with velocity u such that in horizontal range and maximum vertical heights are same.The maximum height is
View Solution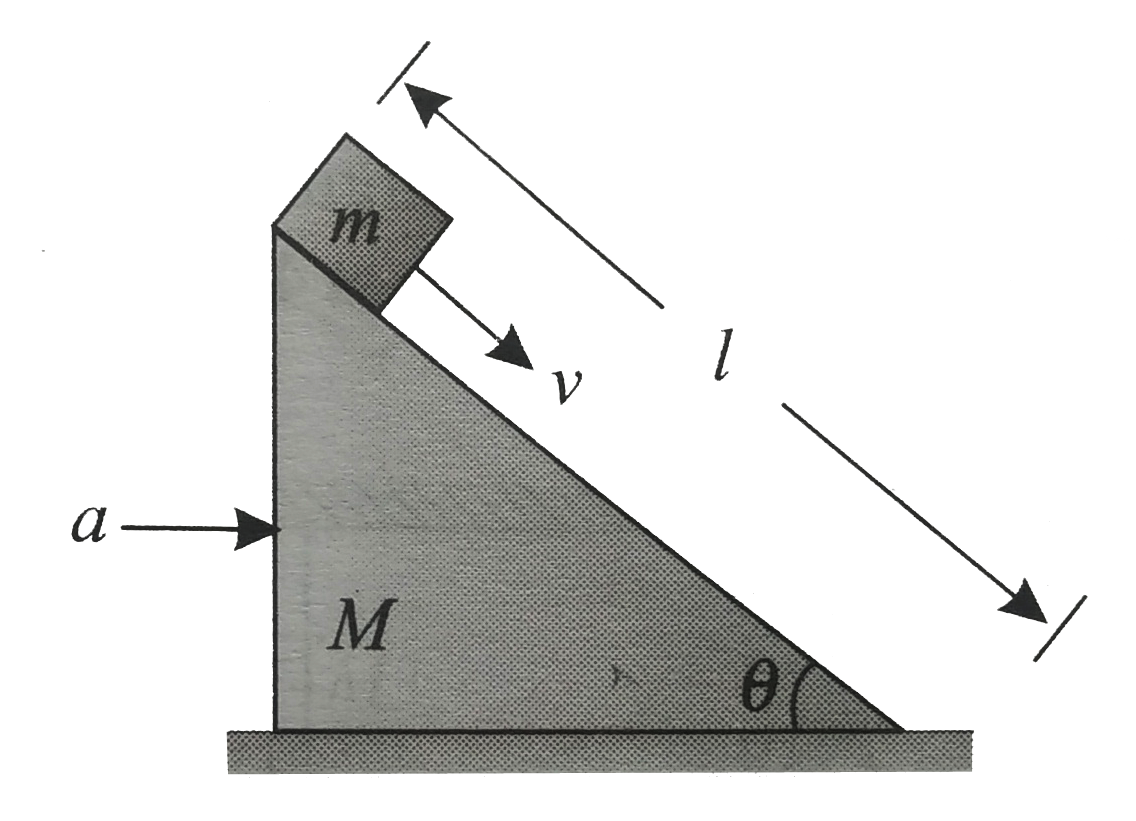
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
The horizontal force applied on the wedge is:
View SolutionA ball is thrown at a speed of 40 m/s at an angle of 600 with the horizontal. Find a. the maximum height reached and b. the range of te ball. Take g=10ms2.
View SolutionThe maximum height attained by a projectile when thrown at an angle θ with the horizontal is found to be half the horizontal range. Then θ is equal to
View SolutionA stone is thrown at an angle θ to the horizontal reaches a maximum height H. Then the time of flight of stone will be:
View Solution

