A projectile is thrown with initial velocity u0 and angle 30∘ with the horizontal. If it remains in the air for 1s. What was its initial velocity ?
19.6ms−1
9.8ms−1
4.9ms−1
1ms−1
The correct Answer is:B
To solve the problem of finding the initial velocity u0 of a projectile thrown at an angle of 30∘ with the horizontal, and which remains in the air for 1 second, we can follow these steps:
Step 1: Understand the Time of Flight Formula
The time of flight T for a projectile is given by the formula:
T=2usinθg
where:
- u is the initial velocity,
- θ is the angle of projection,
- g is the acceleration due to gravity (approximately 9.8m/s2).
Step 2: Substitute the Given Values
In this problem, we know:
- T=1s
- θ=30∘
Substituting these values into the time of flight formula:
1=2u0sin(30∘)g
Step 3: Calculate sin(30∘)
We know that:
sin(30∘)=12
Step 4: Substitute sin(30∘) into the Equation
Now substituting sin(30∘) into the equation:
1=2u0⋅12g
Step 5: Simplify the Equation
This simplifies to:
1=u0g
Step 6: Solve for u0
To find u0, we rearrange the equation:
u0=g
Step 7: Substitute the Value of g
Using g≈9.8m/s2:
u0=9.8m/s2
Conclusion
Thus, the initial velocity u0 of the projectile is:
9.8m/s
The time of flight T for a projectile is given by the formula:
T=2usinθg
where:
- u is the initial velocity,
- θ is the angle of projection,
- g is the acceleration due to gravity (approximately 9.8m/s2).
In this problem, we know:
- T=1s
- θ=30∘
1=2u0sin(30∘)g
We know that:
sin(30∘)=12
Now substituting sin(30∘) into the equation:
1=2u0⋅12g
This simplifies to:
1=u0g
To find u0, we rearrange the equation:
u0=g
Using g≈9.8m/s2:
u0=9.8m/s2
Thus, the initial velocity u0 of the projectile is:
9.8m/s
Topper's Solved these Questions
- MOTIONBook:DC PANDEY ENGLISHChapter:MOTIONExercise:C. Medical entrances gallery
Explore 1 Video
- MEASUREMENT AND ERRORSBook:DC PANDEY ENGLISHChapter:MEASUREMENT AND ERRORSExercise:Subjective
Explore 19 Videos
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:(C )Medical entrances gallery
Explore 32 Videos
Similar Questions
A projectile is thorwn with a velocity of 50ms−1 at an angle of 53∘ with the horizontal
Choose the incorrect statement (A) It travels vertically with a velocity of 40 ms–1 (B) It travels horizontally with a velocity of 30 ms–1 (C) The minimum velocity of the projectile is 30 ms–1 (D) None of these
View SolutionTwo particle are projected with same initial velocities at an angle 30∘ and 60∘ with the horizontal .Then
View Solution
Knowledge Check
A body is thrown with a velocity of 9.8 m/s making an angle of 30∘ with the horizontal. It will hit the ground after a time
A3 sB2sC1.5 sD1 s
A projectile is thrown with a velocity of 20 m/s, at an angle of 60∘ with the horizontal. After how much time the velocity vector will make an angle of 45∘ with the horizontal (in upward direction) is (take g=10m/s2)−
View SolutionA body is thrown into air with a velocity 5 m/s making an angle 30∘ with the horizontal .If the vertical component of the velocity is 5 m/s what is the velocity of the body ? Also find the horizontal component .
View SolutionA rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.
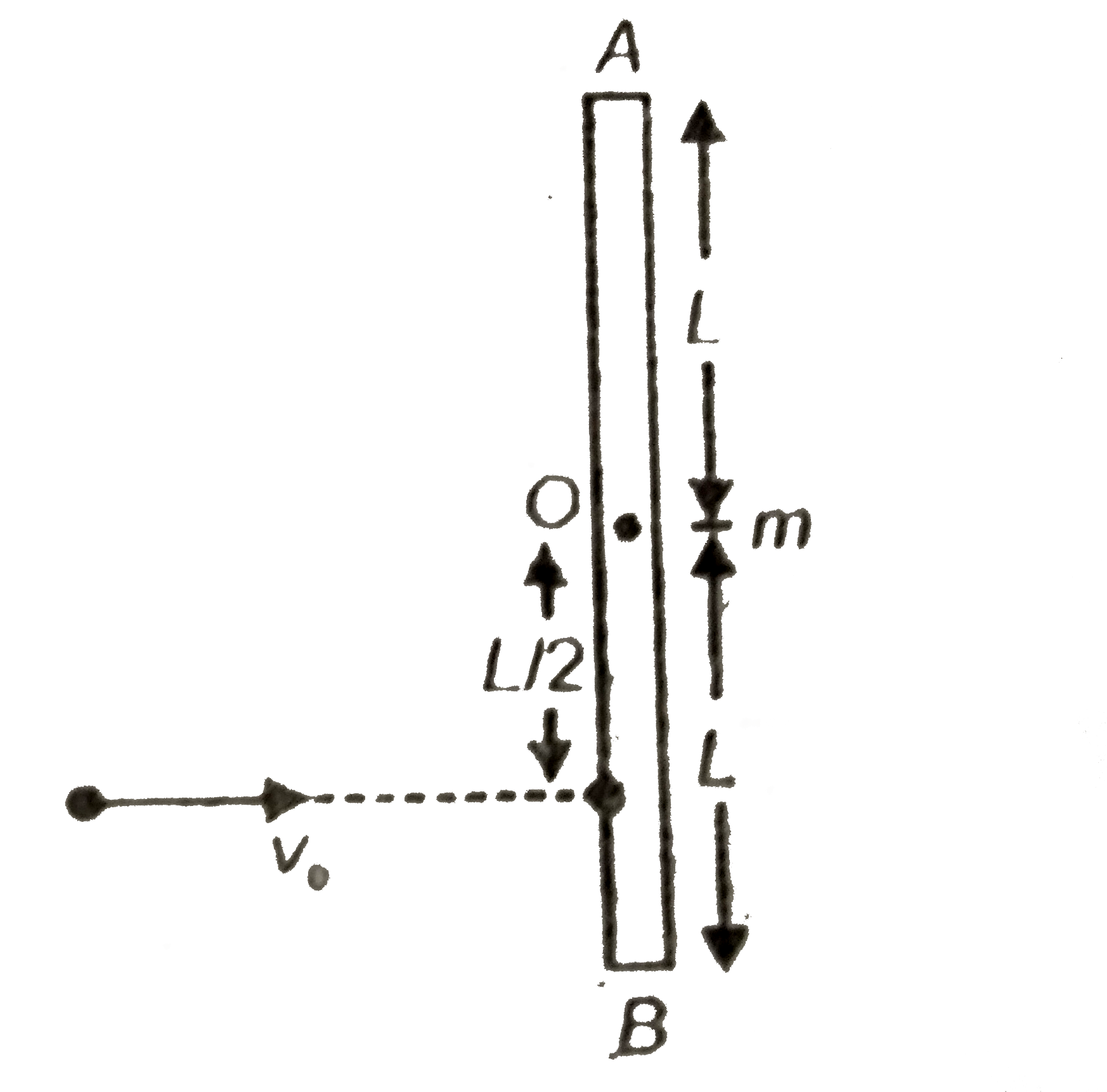
Distance of point P on rod from B which is at rest immediately afte collision is
View SolutionTwo projectiles thrown from the same point at angles 60∘and30∘ with the horizontal attain the same height. The ratio of their initial velocities is
View SolutionA projectile projected with initial velocity 20m/s and at and angle of 30∘ from horizontal. Find the total work done when it will hit the ground.
View SolutionA projectile is thrown with velocity v at an angle θ with the horizontal. When the projectile is at a height equal to half of the maximum height,.
The vertical component of the velocity of projectile is.
View SolutionA projectile is thrown with velocity v at an angle θ with the horizontal. When the projectile is at a height equal to half of the maximum height,.
The velocity of the projectile when it is at a height equal to half of the maximum height is.
View Solution