A cracker is thrown into air with a velocity of 10m/s at an angle of 45∘ with the vertical. When it is at a height of 0.5m from the ground, it explodes into a number of pieces which follow different parabolic paths. What is the velocity of centre of mass, when it is at a height of 1m from the ground? (g=10m/s2)
4√5ms−1
2√5ms−1
5√4ms−1
5ms−1
The correct Answer is:A
To solve the problem step by step, we will analyze the motion of the cracker before and after it explodes, focusing on the center of mass.
Step 1: Determine the initial velocity components
The cracker is thrown with an initial velocity u=10m/s at an angle of 45∘ with the vertical. We can find the horizontal (ux) and vertical (uy) components of the initial velocity.
- Since the angle is with respect to the vertical, we have:
ux=usin(45∘)=10⋅1√2=10√2m/s
uy=ucos(45∘)=10⋅1√2=10√2m/s
Step 2: Analyze the motion at the height of 1 meter
The cracker explodes at a height of 0.5m and we need to find the velocity of the center of mass when it reaches a height of 1m.
Step 3: Calculate the vertical velocity at height 1 meter
To find the vertical velocity (vy) at height 1m, we can use the kinematic equation:
v2y=u2y−2gs
where:
- g=10m/s2 (acceleration due to gravity)
- s=1m−0.5m=0.5m (displacement)
Substituting the values:
v2y=(10√2)2−2⋅10⋅0.5
v2y=1002−10=50−10=40
vy=√40=2√10m/s
Step 4: Determine the horizontal velocity
The horizontal velocity (vx) remains constant since there are no horizontal forces acting on the cracker:
vx=ux=10√2m/s
Step 5: Calculate the magnitude of the velocity of the center of mass
Now, we can find the magnitude of the velocity of the center of mass using the Pythagorean theorem:
vcm=√v2x+v2y
Substituting the values:
vcm=
⎷(10√2)2+(2√10)2
=√50+40=√90=3√10m/s
Final Answer
The velocity of the center of mass when it is at a height of 1m from the ground is 3√10m/s.
---
The cracker is thrown with an initial velocity u=10m/s at an angle of 45∘ with the vertical. We can find the horizontal (ux) and vertical (uy) components of the initial velocity.
ux=usin(45∘)=10⋅1√2=10√2m/s
uy=ucos(45∘)=10⋅1√2=10√2m/s
The cracker explodes at a height of 0.5m and we need to find the velocity of the center of mass when it reaches a height of 1m.
To find the vertical velocity (vy) at height 1m, we can use the kinematic equation:
v2y=u2y−2gs
where:
- g=10m/s2 (acceleration due to gravity)
- s=1m−0.5m=0.5m (displacement)
v2y=(10√2)2−2⋅10⋅0.5
v2y=1002−10=50−10=40
vy=√40=2√10m/s
The horizontal velocity (vx) remains constant since there are no horizontal forces acting on the cracker:
vx=ux=10√2m/s
Now, we can find the magnitude of the velocity of the center of mass using the Pythagorean theorem:
vcm=√v2x+v2y
Substituting the values:
vcm=
⎷(10√2)2+(2√10)2
=√50+40=√90=3√10m/s
The velocity of the center of mass when it is at a height of 1m from the ground is 3√10m/s.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Match the coloumns
9 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Check points
50 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
Find the energy possessed by an object of mass 10 kg when it is at a height of 6 m above the ground.Given, g=9.8m/s2
View SolutionA body is thrown vertically upward from a point A 125 m above the ground. It goes up to a maximum height of 250 m above the ground and passes through A on its downward journey. The velocity of the body when it is at a height of 70 m above the ground is (g=10m/s2)
View Solution
Knowledge Check
A ball is thrown from the top of a tower with an initial velocity of 10m/s at an angle of 30∘above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower (g=10m/s2) will be
A5 mB20 mC15 mD10 m
A particle is projected from ground with velocity 20(√2)m/s at 45∘. At what time particle is at height 15 m from ground? (g=10m/s2)
View SolutionA balloon is going upwards with velocity 12m/sec it releases a packet when it is at a height of 65 m from the ground. How much time the packet will take to reach the ground (g=10m/sec2)
View SolutionA stone released with zero velocity from the top of a tower, reaches the ground in 4s. The height of the tower is (g=10m/s2)
View SolutionA ball is thrown from the top of 36m high tower with velocity 5m/ss at an angle 37∘ above the horizontal as shown. Its horizontal distance on the ground is closest to [g=10m/s2
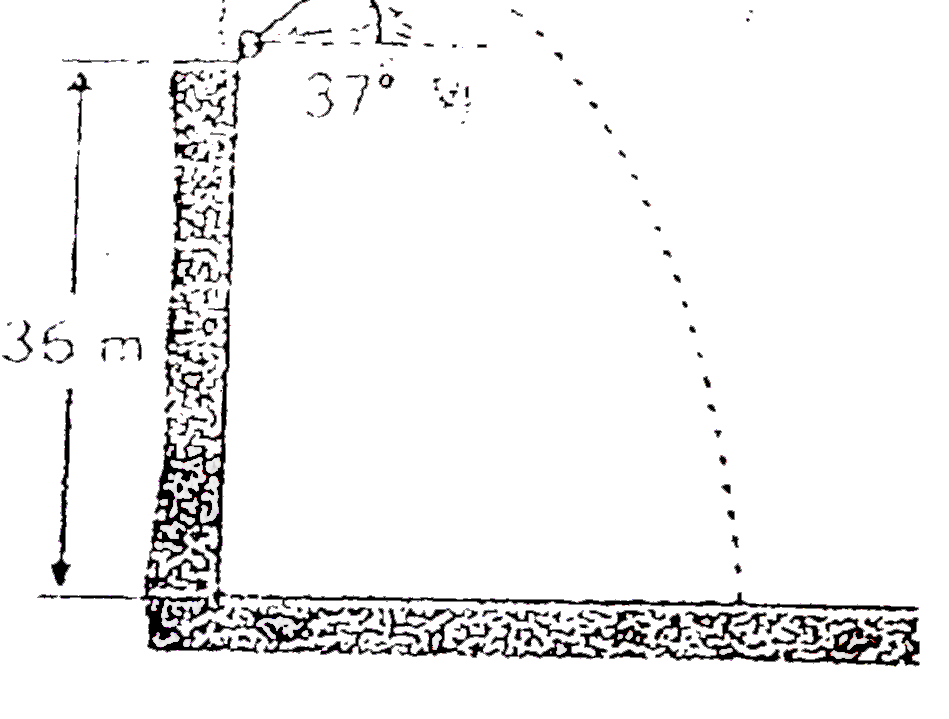 :
:
View SolutionA fighter plane moving with a speed of 50√2ms−1 upward at an angle of 45∘ with the vertical releases a bomb when it was at a height 1000m from ground. Find (a) the time of flight
(b) the maximum height of the bomb above ground.
View SolutionA body is projected horizontally from the top of a tower with a velocity of 10m/s. If it hits the ground at an angle of 45∘, the vertical component of velocity when it hits ground in m/s is
View SolutionA body is projected horizontally from the top of a tower with a velocity of 10m/s.If it hits the ground at an angle 45∘, then vertical component of velocity when it hits ground in m/s is
View Solution
