A bullet moving with a speed of 100ms−1 can just penetrate into two planks of equal thickness. Then the number of such planks, if speed is doubled will be .
4
8
6
10
The correct Answer is:C
To solve the problem step-by-step, we will analyze the motion of the bullet as it penetrates the planks and how the distance it travels relates to its speed.
Step 1: Understand the Initial Conditions
The bullet penetrates 2 planks of equal thickness at an initial speed of 100m/s. Let the thickness of each plank be B. Therefore, the total distance the bullet travels through the planks is 2B.
Step 2: Use the Kinematic Equation
We can use the kinematic equation for uniformly decelerated motion:
v2=u2−2as
where:
- v is the final velocity (0, since the bullet stops),
- u is the initial velocity (100 m/s),
- a is the deceleration,
- s is the distance traveled (which is 2B).
Rearranging the equation gives us:
0=(100)2−2a(2B)
This simplifies to:
10000=4aB
From this, we can express a:
a=100004B=2500B
Step 3: Analyze the New Conditions
Now, if the speed of the bullet is doubled, the new speed u′=200m/s. We want to find out how many planks the bullet can penetrate at this new speed.
Step 4: Apply the Kinematic Equation Again
Using the same kinematic equation for the new speed:
v2=u′2−2as′
where s′ is the new distance traveled. Setting v=0 gives us:
0=(200)2−2as′
This simplifies to:
40000=2as′
Substituting a=2500B into the equation:
40000=2(2500B)s′
This simplifies to:
40000=5000s′B
Rearranging gives:
s′=40000B5000=8B
Step 5: Calculate the Number of Planks
Since each plank has a thickness B, the number of planks N that can be penetrated is:
N=s′B=8BB=8
Conclusion
Thus, if the speed of the bullet is doubled, it can penetrate 8 planks.
---
The bullet penetrates 2 planks of equal thickness at an initial speed of 100m/s. Let the thickness of each plank be B. Therefore, the total distance the bullet travels through the planks is 2B.
We can use the kinematic equation for uniformly decelerated motion:
v2=u2−2as
where:
- v is the final velocity (0, since the bullet stops),
- u is the initial velocity (100 m/s),
- a is the deceleration,
- s is the distance traveled (which is 2B).
0=(100)2−2a(2B)
This simplifies to:
10000=4aB
From this, we can express a:
a=100004B=2500B
Now, if the speed of the bullet is doubled, the new speed u′=200m/s. We want to find out how many planks the bullet can penetrate at this new speed.
Using the same kinematic equation for the new speed:
v2=u′2−2as′
where s′ is the new distance traveled. Setting v=0 gives us:
0=(200)2−2as′
This simplifies to:
40000=2as′
Substituting a=2500B into the equation:
40000=2(2500B)s′
This simplifies to:
40000=5000s′B
Rearranging gives:
s′=40000B5000=8B
Since each plank has a thickness B, the number of planks N that can be penetrated is:
N=s′B=8BB=8
Thus, if the speed of the bullet is doubled, it can penetrate 8 planks.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Match the coloumns
9 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Check points
50 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
A bullet moving with a speed of 100 m/s can just penetrate two planks of equal thickness. Now if the speed is doubled, then the number of such planks required to stop the bullet will be
View SolutionA bullet moving with a speed of 150ms−1 strikes a tree and penetrates 3.5 cm before stopping. What is the magnitude of its retardation in the tree and the time taken for it to shop after striking the tree?
View SolutionA bullet moving with a velocity of 30√2ms−1 is fired into a fixed target. It penetrated into the target to the extent of s metres. If the same bullet is fired into a target of thickness s2 metres and of the same material with the same velocity, then the bullet comes out of the target with velocity
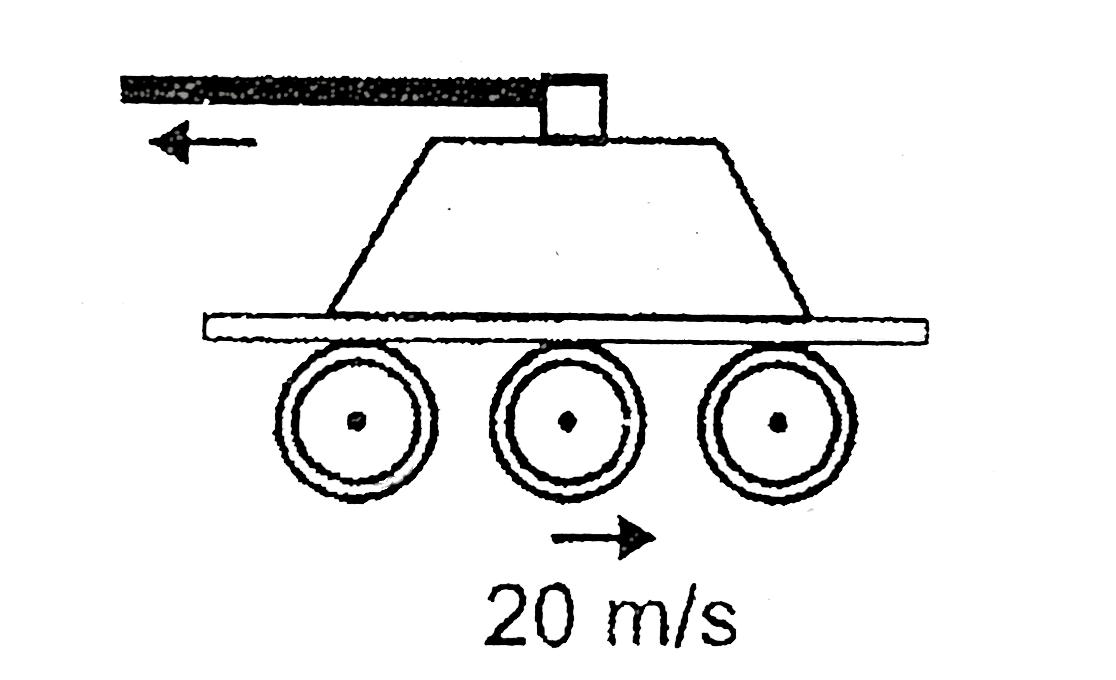
View SolutionA machine gun is mounted on an armored car moving with a speed of 20ms−1. The gun point against the direction of motion of car. The muzzle speed of bullet is equal to speed of sound in air i.e., 340ms−1. The time difference between bullet actually reaching and sound of firing reaching at a target 544m away from car at the instant of firing is reaching at a target 544m away from car at the instant of firing is
View SolutionIn CID serial (on TV), Abhijeet fires a bullet of mass 100 g with a speed of 100ms−1 on a soft plywood of thickness 4 cm the bullet emerges with 10% of its initial KE. Find the emergent speed of the bullet.
View SolutionA bullet of mass 20 g has an initial speed of 1ms−1 just before it starts penetrating a mud wall of thickness 20 cm. If the wall offers a mean resistance of 2.5×10−2N the speed of the bullet after emerging from the other side of the wall is close to:
View SolutionA bullet of mass 20 g has a n initial speed of 1ms−1 just before it starts penetrating a mud wall of thichness 20cm. If the wall offers a mean resistance of 2.5×10−2N the speed of the bullet after emerging from the other side of the wall is close to:
View Solutionbullets are fixed at regualr intervals of 10 second from a car moving with a speed of 30ms−1 towards another car approaching with a speed of 60 m/s . The interval at which the firing can be reported is (Speed of sound = 330ms−1
View SolutionA bullet of mass 50 g enters a block of thickness t with speed of 500 ms−1. It emerges with 4% of its initial kinetic energy. The emergent speed is
View SolutionA 10 g bullet moving at 200 m/s stops after penetrating 5 cm of wooden plank. The average force exerted on the bullet will be
View Solution
