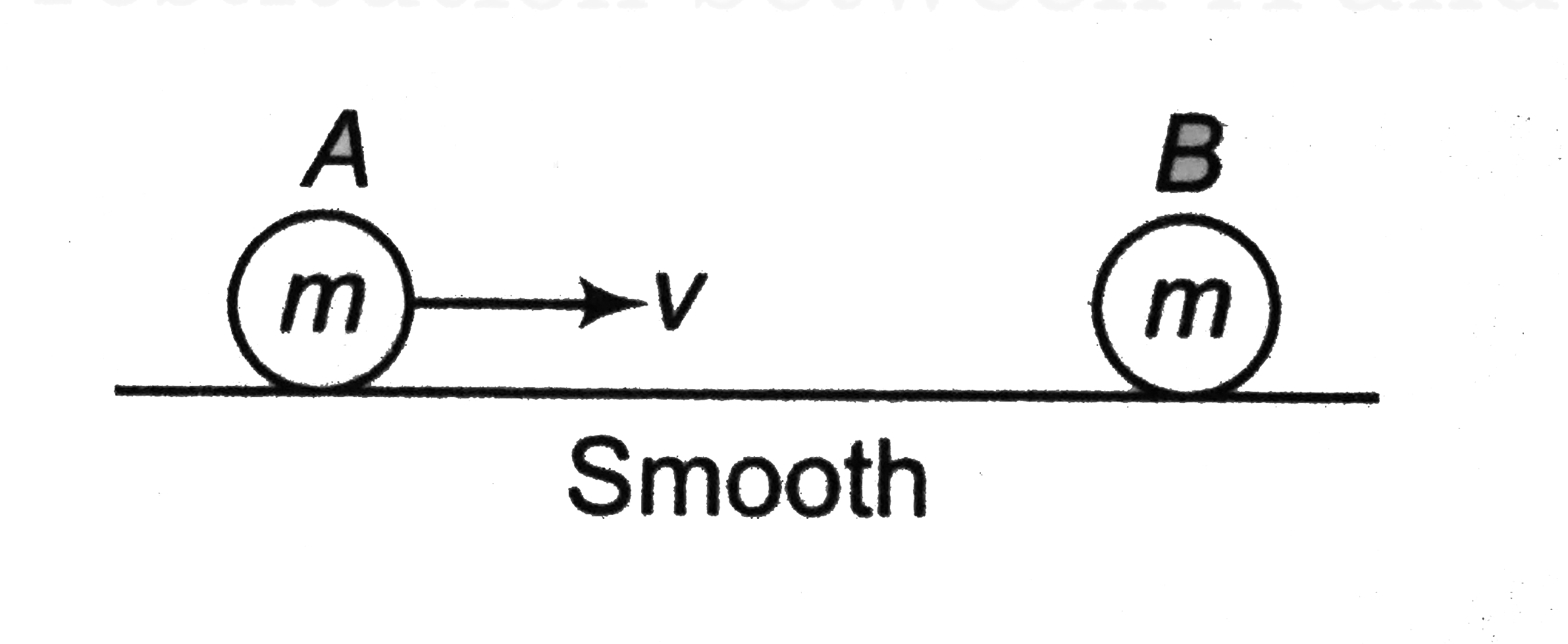
In a one-dimensional collision between two identical particles. A and B, B is stationary and A has momentum p before impact. During impact, B gives an impulse J to A. Find the coefficient of restitution between A and B?
2Jp−1
2Jp+1
(Jp)+1
(Jp)−1
The correct Answer is:A
To solve the problem of finding the coefficient of restitution between two identical particles A and B during a one-dimensional collision, we can follow these steps:
Step 1: Understand the Initial Conditions
- Particle A has an initial momentum p and is moving towards particle B, which is stationary.
- The mass of both particles is m.
Step 2: Determine Initial Velocities
- The initial velocity of particle A can be expressed as:
vA=pm
- The initial velocity of particle B is:
vB=0
Step 3: Analyze the Impulse Given
- During the impact, particle B gives an impulse J to particle A.
- By the principle of conservation of momentum, the final momentum of A after receiving the impulse can be written as:
p′A=p+J
- The final velocity of particle A, v′A, can be expressed as:
v′A=p+Jm
Step 4: Determine the Final Velocity of Particle B
- Since particle A imparts an equal and opposite impulse to particle B, the impulse on B is also J.
- The final momentum of particle B can be expressed as:
p′B=J
- The final velocity of particle B, v′B, is:
v′B=Jm
Step 5: Calculate the Coefficient of Restitution
- The coefficient of restitution e is defined as the ratio of the relative velocity of separation to the relative velocity of approach:
e=Velocity of separationVelocity of approach
- The velocity of approach (before collision) is:
vapproach=vA−vB=pm−0=pm
- The velocity of separation (after collision) is:
vseparation=v′B−v′A=Jm−p+Jm=J−(p+J)m=−pm
- Therefore, the coefficient of restitution can be calculated as:
e=−pmpm=−pp=−1
Step 6: Final Expression for Coefficient of Restitution
- Since we are interested in the magnitude, we take the absolute value:
e=1
Final Answer
The coefficient of restitution between particles A and B is:
e=2Jp−1
- Particle A has an initial momentum p and is moving towards particle B, which is stationary.
- The mass of both particles is m.
- The initial velocity of particle A can be expressed as:
vA=pm
- The initial velocity of particle B is:
vB=0
- During the impact, particle B gives an impulse J to particle A.
- By the principle of conservation of momentum, the final momentum of A after receiving the impulse can be written as:
p′A=p+J
- The final velocity of particle A, v′A, can be expressed as:
v′A=p+Jm
- Since particle A imparts an equal and opposite impulse to particle B, the impulse on B is also J.
- The final momentum of particle B can be expressed as:
p′B=J
- The final velocity of particle B, v′B, is:
v′B=Jm
- The coefficient of restitution e is defined as the ratio of the relative velocity of separation to the relative velocity of approach:
e=Velocity of separationVelocity of approach
- The velocity of approach (before collision) is:
vapproach=vA−vB=pm−0=pm
- The velocity of separation (after collision) is:
vseparation=v′B−v′A=Jm−p+Jm=J−(p+J)m=−pm
- Therefore, the coefficient of restitution can be calculated as:
e=−pmpm=−pp=−1
- Since we are interested in the magnitude, we take the absolute value:
e=1
The coefficient of restitution between particles A and B is:
e=2Jp−1
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Match the coloumns
9 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Check points
50 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
In a one dimensional collision between two identical particles A and B, B is stationary and A has momentum p before impact. During impact, B gives impulse J to A.
View SolutionIn one dimentional collision between two idential particles 'A' and 'B'. 'B' is stationary and 'A' has momentum 54 kg-m/ sec before impact. During impact , 'B' gives an impulse 3kg-m/sec to 'A' . The coefficient of restitution between A and B is
View Solution
Knowledge Check
In an elastic one dimensional collision between two particles the relative veloctiy of approach before collision is
Agreater than the relative velocity of separation after collisionBless than the relative velocity of separation after collisionCequal to the relative velocity of separation after collisionDless than the relative velocity of separation if the incoming particle is heavier than the target particle
In a head on collision between two identical particles A and B moving on a horizontal surface, B is stationary and A has momentum P0 before impact. Due to the impact, A recrieves an impulse I. Then coefficient of restitution between the two is :
View SolutionIn the figure shown, coefficient of restitution between A and B is e=12, then
View SolutionA body X with a momentum p collides with another identical stationary body Y one dimensionally. During the collision, Y gives an impulse J to body X. Then coefficient of restitution is
View SolutionFind the single arithmetic mean between: (a−b)and(a+b)
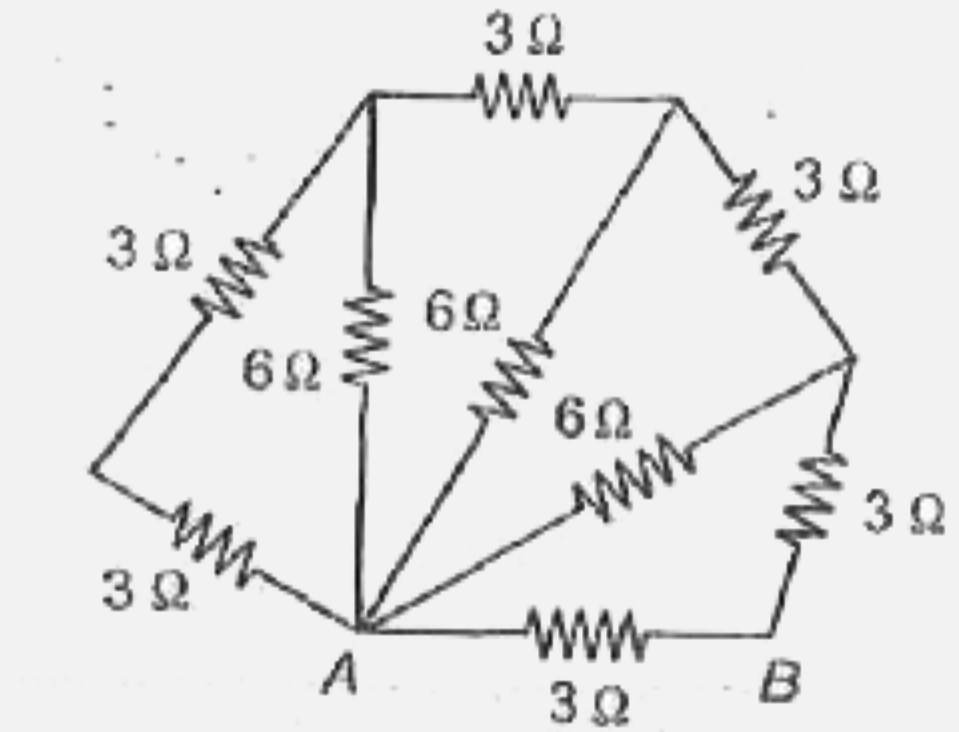
View SolutionFind the equivalent resistance between A and B in the give figure .
View SolutionA sphere A of mass m, travelling with speed v, collides directly with a stationary sphere B. If A is brought to rest and B is given a speed V, find (a) the mass of B (b) the coefficient of restitution between A and B?
View SolutionTwo billiard balls of same size and mass are in contact on a billiard table. A third ball of same mass and size strikes them symmetrically and remains at rest after the impact. Find the coefficient of restitution between the balls?
View Solution
