A solid glass sphere with radius R and an index of refraction 1.5 is silvered over one hemisphere. A small object is located on the axis of the sphere at a distance 2R to the left of the vertex of the unsilvered hemisphere. Find the position of final image after all refractions and reflection have taken place.
To solve the problem of finding the position of the final image formed by a solid glass sphere with a silvered hemisphere, we will follow these steps:
Step 1: Understand the Setup
We have a solid glass sphere with radius R and an index of refraction n=1.5. One hemisphere is silvered, and a small object is located on the axis of the sphere at a distance 2R to the left of the vertex of the unsilvered hemisphere.
Step 2: Identify the Object Distance
The object distance U from the vertex of the unsilvered hemisphere is −2R (negative because it is to the left of the vertex).
Step 3: Apply the Refraction Formula
For the unsilvered surface (the first surface), we can use the formula for refraction at a spherical surface:
n2V−n1U=n2−n1R
Here, n2=1 (air), n1=1.5 (glass), and R=R (radius of the sphere).
Substituting the values:
1V−1.5−2R=1−1.5R
This simplifies to:
1V+1.52R=−0.5R
Rearranging gives:
1V=−0.5R−1.52R=−0.5+0.75R=−1.25R
Thus,
V=−R1.25=−4R5
This means the image formed by the first refraction is at a distance of 4R5 to the left of the vertex of the unsilvered hemisphere.
Step 4: Determine the Object Distance for the Silvered Hemisphere
The image formed by the first refraction acts as the object for the silvered hemisphere. The distance from the vertex of the silvered hemisphere to this image is:
Distance from vertex of silvered hemisphere=2R−4R5=10R−4R5=6R5
This distance is positive since it is to the right of the vertex of the silvered hemisphere.
Step 5: Apply the Reflection Formula
Now we apply the reflection formula for the silvered surface:
n2V′−n1U′=n2−n1R
Here, n2=1.5 (glass), n1=1 (air), and U′=6R5.
Substituting the values:
1.5V′−16R5=1.5−1R
This simplifies to:
1.5V′−56R=0.5R
Rearranging gives:
1.5V′=0.5R+56R=3+56R=86R=43R
Thus,
V′=1.5R4=3R8
This means the final image is located at a distance of 3R8 to the right of the vertex of the silvered hemisphere.
Final Answer
The final image is formed at a distance of 3R8 from the vertex of the silvered hemisphere.
---
We have a solid glass sphere with radius R and an index of refraction n=1.5. One hemisphere is silvered, and a small object is located on the axis of the sphere at a distance 2R to the left of the vertex of the unsilvered hemisphere.
The object distance U from the vertex of the unsilvered hemisphere is −2R (negative because it is to the left of the vertex).
For the unsilvered surface (the first surface), we can use the formula for refraction at a spherical surface:
n2V−n1U=n2−n1R
Here, n2=1 (air), n1=1.5 (glass), and R=R (radius of the sphere).
1V−1.5−2R=1−1.5R
This simplifies to:
1V+1.52R=−0.5R
Rearranging gives:
1V=−0.5R−1.52R=−0.5+0.75R=−1.25R
Thus,
V=−R1.25=−4R5
This means the image formed by the first refraction is at a distance of 4R5 to the left of the vertex of the unsilvered hemisphere.
The image formed by the first refraction acts as the object for the silvered hemisphere. The distance from the vertex of the silvered hemisphere to this image is:
Distance from vertex of silvered hemisphere=2R−4R5=10R−4R5=6R5
This distance is positive since it is to the right of the vertex of the silvered hemisphere.
Now we apply the reflection formula for the silvered surface:
n2V′−n1U′=n2−n1R
Here, n2=1.5 (glass), n1=1 (air), and U′=6R5.
1.5V′−16R5=1.5−1R
This simplifies to:
1.5V′−56R=0.5R
Rearranging gives:
1.5V′=0.5R+56R=3+56R=86R=43R
Thus,
V′=1.5R4=3R8
This means the final image is located at a distance of 3R8 to the right of the vertex of the silvered hemisphere.
The final image is formed at a distance of 3R8 from the vertex of the silvered hemisphere.
Topper's Solved these Questions
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Exercise 31.1
Explore 3 Videos
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Exercise 31.2
Explore 2 Videos
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Example Type 11
Explore 3 Videos
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
- SEMICONDUCTORSBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORSExercise:Subjective
Explore 12 Videos
Similar Questions
A glass hemisphere of radius R and of material having refractive index 1.5 is silvered on its flat face as shown in figure., A small object of height h is located at a distance 2R from the surface of hemisphere as shown in the figure. The final image will form.

View SolutionA hemispherical portion of the surface of a solid glass sphere (mu = 1.5) of radius r is silvered to make the inner side reflecting. An object is placed on the axis of the hemisphere at a distance 3r from the centre of the sphere. The light from the object is refracted at the unsilvered part, then reflected from the silvered part and again refracted at the unsilvered part. Locate the final image formed.
View SolutionIn the figure shown , a point object O is placed in air on the principal axis. The radius of curvature of the spherical surfaces is 60cm. I is the final image formed after all reflections and refractions.
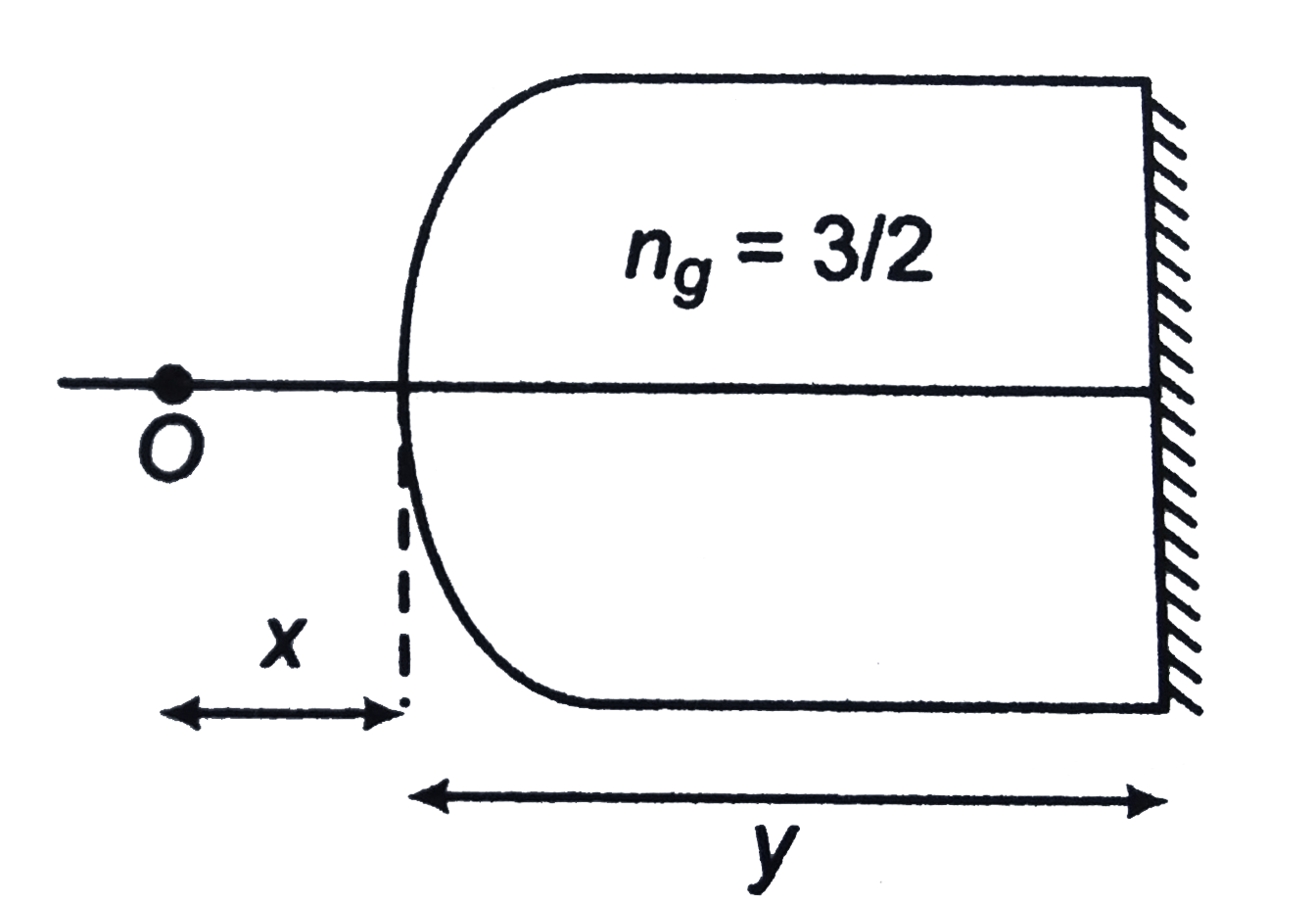
View SolutionA glass hemispher of refractive index 4/3 and of radius 4cm is placed on a plane mirror. A point object is placed on axis of this sphere at a distance 'd' from O as shown in the figure. If the final image is formed at infinity, then find the value of d in mm .

View SolutionA point object is situated at a distance of 36 cm from the centre of the sphere of radius 12 cm and refractive index 1.5. Locate the position of the image due to refraction through sphere.
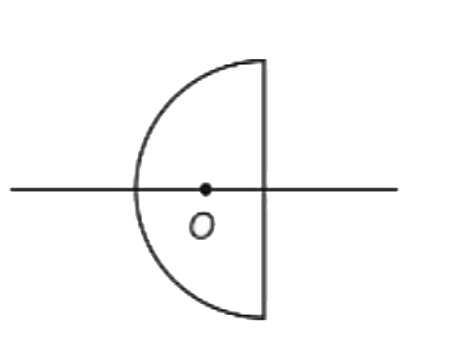
View SolutionA glass hemisphere (μ=1.5) has a radius of curvature of 16 cm. A small object O is located on its axis halfway between the plane and spherical surface. The distance between two images , when viewed along the axis from the sides of the hemisphere is
View SolutionDoes the escape speed of a body from the earth depend on.
(i)mass of the body
(ii)the location from where it is projected
(iii)the direction of projection
(iv)the height of the location from where the body is launched?
View Solution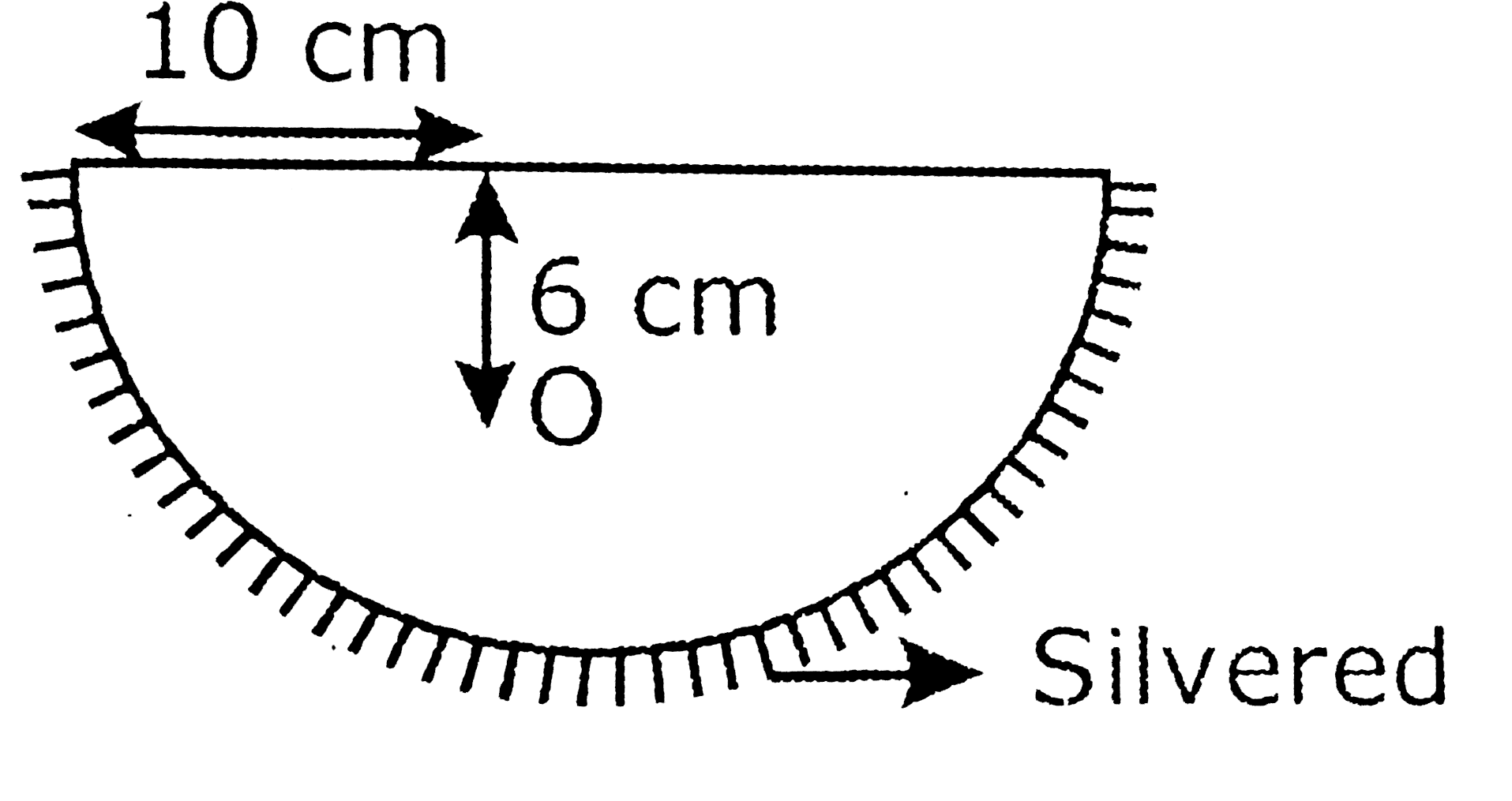
A hemispherical glass body of radius 10 cm and refractive index 1.5 is silvered on its curved surface . A small air bubble is 6 cm below the flat surface inside it along the axis. The position of the image of the air bubble made by the mirror is seen :
View SolutionAn object is at a distance of d=2.5cm from the surface of a glass sphere with a radius R=10cm. Find the position of the final image produced by the sphere. The refractive index of glass is μ=1.5.
View SolutionConsider a sphere of radius R made of glass of refractive index μ. A small object moves along the dismeter with a constant velocity u. Find the velocity of the image as seen by an observer outside when the object passes through center.
View Solution

