Given that .1μ2=4/3,.2μ3=3/2. Find .1_μ3.
The correct Answer is:B
To solve the problem, we need to find the refractive index μ1μ3 given the relationships μ1μ2=43 and μ2μ3=32.
1. Write down the given equations:
- From the problem, we have:
μ1μ2=43(Equation 1)
μ2μ3=32(Equation 2)
2. Rearrange Equation 1 to express μ2:
- From Equation 1, we can express μ2 in terms of μ1:
μ2=43μ1(Equation 3)
3. Substitute Equation 3 into Equation 2:
- Now, substitute μ2 from Equation 3 into Equation 2:
(43μ1)μ3=32
4. Solve for μ3:
- Multiply both sides by 3μ1 to eliminate the fraction:
4μ3=32⋅3μ1
4μ3=92μ1
- Now, divide both sides by 4:
μ3=98μ1
5. Find μ1μ3:
- Now, we can find μ1μ3:
μ1μ3=μ1⋅(98μ1)=98μ21
6. Final Result:
- Therefore, the final relationship we have is:
μ1μ3=98
Summary:
The value of μ1μ3 is 98.
- From the problem, we have:
μ1μ2=43(Equation 1)
μ2μ3=32(Equation 2)
- From Equation 1, we can express μ2 in terms of μ1:
μ2=43μ1(Equation 3)
- Now, substitute μ2 from Equation 3 into Equation 2:
(43μ1)μ3=32
- Multiply both sides by 3μ1 to eliminate the fraction:
4μ3=32⋅3μ1
4μ3=92μ1
- Now, divide both sides by 4:
μ3=98μ1
- Now, we can find μ1μ3:
μ1μ3=μ1⋅(98μ1)=98μ21
- Therefore, the final relationship we have is:
μ1μ3=98
The value of μ1μ3 is 98.
Topper's Solved these Questions
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Exercise 31.2
Explore 2 Videos
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Introductory exercise
Explore 4 Videos
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Solved Example
Explore 15 Videos
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
- SEMICONDUCTORSBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORSExercise:Subjective
Explore 12 Videos
Similar Questions
Knowledge Check
A double convex lens, lens made of a material of refractive index μ1, is placed inside two liquids or refractive indices μ2 and μ3, as shown. μ2>μ1>μ3. A wide, parallel beam of light is incident on the lens from the left. The lens will give rise to
 Aa single convergent beamBtwo different convergent beamsCtwo different divergent beamsDa convergent and a divergent beam.
Aa single convergent beamBtwo different convergent beamsCtwo different divergent beamsDa convergent and a divergent beam.
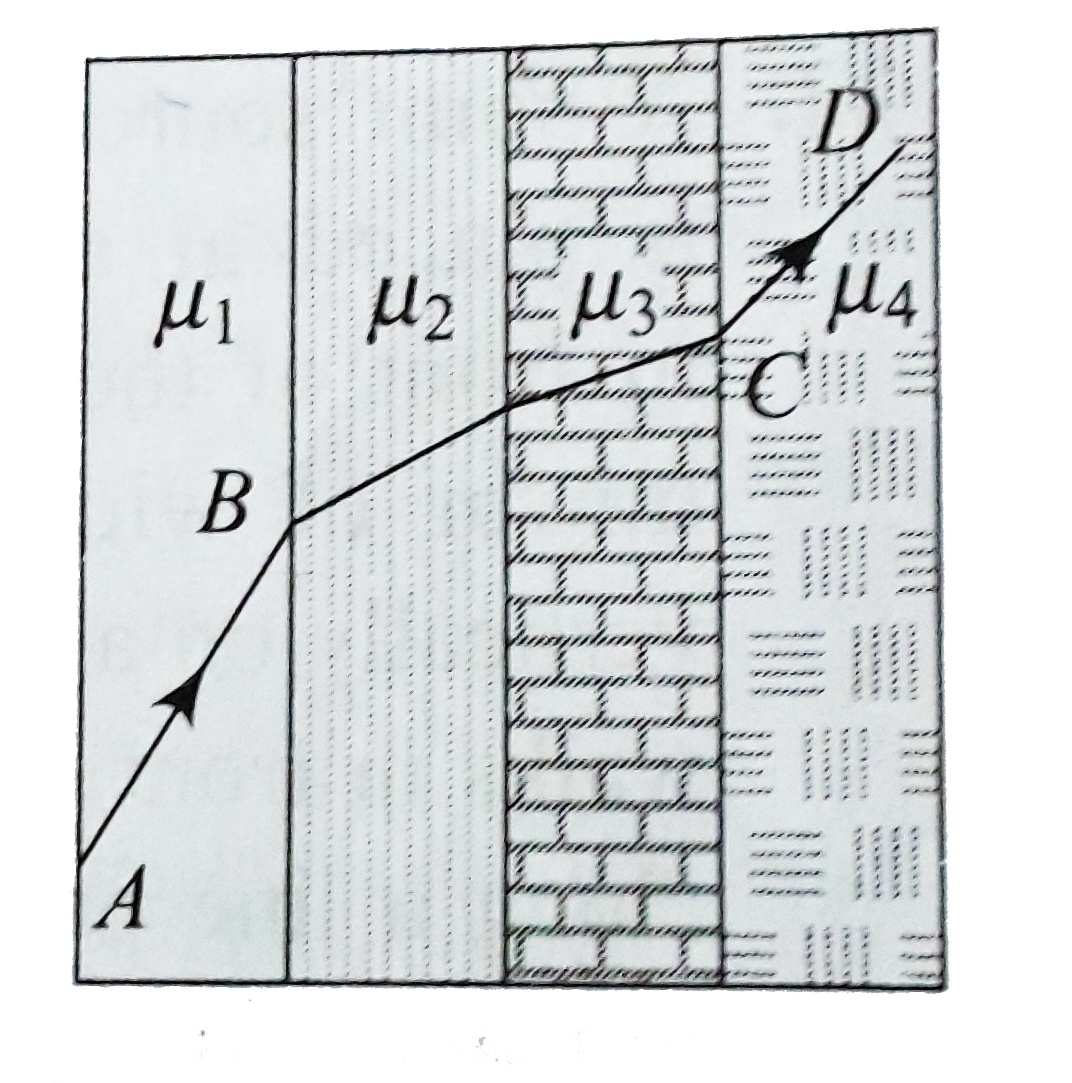
A ray of light passes through four transpar ent media with refractive indicesμ1,μ2,μ3 and μ4 as shown in figure. The surfaces of all media are parallel. If the emergent ray is parallel to the incident ray, we must hav
View SolutionA ray of light passes through four transparent media with refractive indices μ1,μ2,μ3,andμ4 as shown in figure. The surfaces of all media are paralle. If the emerent ray CD is parallel to the incident ray AB, we must have
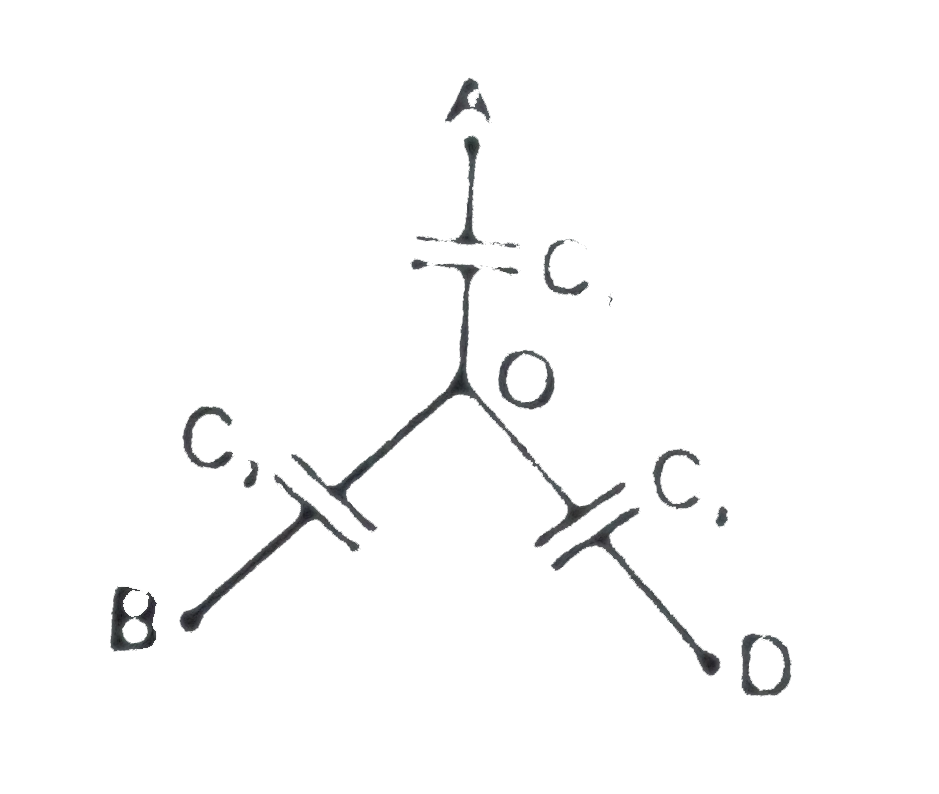
View SolutionThree uncharged capacitors of capacitance C1=1μF,C2=2μF and C3=3μF are connected as shown in the figure. The potential of point A, B and D are 10 volt, 25 volt and 20 volt respectively. Determine the potential at point O.
View SolutionFocal length of a convex lense in air is 10cm. Find its focal
length in water. Given that μg=3/2 and μw=4/3.
View SolutionFocal length of a convex lense in air is 10cm. Find its focal
length in water. Given that μg=3/2 and μw=4/3.
View SolutionThere are three optical media 1,2 and 3 with their refractive index μ1, μ2 and μ3 such that μ1>μ2>μ3 choose the correct options (TIR means total internal reflection)
View SolutionA right angled prism of refractive index μ1 is placed in a rectangular block of refractive index μ2 , which is surrounded by a medium of refractive index μ3 ,as shown in the figure . A ray of light 'e' enters the rectangular block at normal incidence . depending upon the relationship between μ1,μ2andμ3 , it takes one of the four possible paths 'ef' , 'eg' , 'eh' or 'ef'
_E01_228_Q01.png)
Match the paths in List I with conditions of refractive indices in List II and select the correct answer using the codes given below the lists:
{:("List" I , "List" II) , ( P. e rarr f , 1. mu_(1)gt sqrt(2mu_(2))) , ( Q. e rarr g , 2. mu_(2) gt mu_(1) "and" mu_(2) gt mu_(3)), ( R. e rarr f , 3. mu_(1) = mu_(2)), ( S. e rarr f , 4. mu_(2) lt mu_(1) lt sqrt(2mu_(2)) "and" mu_(2) gt mu_(3)):}<br>Codes:<br>{:( P , Q , R , S) , ((A) 2 , 3 , 1 , 4), ((B) 1 , 2 , 4 , 3) , ((C) 4 , 1 , 2 , 3) , ((D) 2, 3 , 4 , 1):}
View Solution