Suppose a verticle tunnel is dug along the diametal of earth , which is assumed to be a sphere of unifrom mass density ρ. If a body of mass m is throws in this tunal, its acceleration at a distance y from the centre is given by

4π3GρYm
34πρY
43πρY
43πGρY
The correct Answer is:D
a=E=(GMR3Y (as a=E=Fm)
=G(43πR3ρ)R3y=43πGρy
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 More Than One Correct
10 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 Subjective
14 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 1 Subjective
19 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Suppose a vertical tunnel is dug along the diameter of earth , which is assumed to be a sphere of uniform mass density ρ. If a body of mass m is thrown in this tunnel, its acceleration at a distance y from the centre is given by

View SolutionIf earth is assumed to be a sphere of uniform density then plot a graph between acceleration due to gravity (g) and distance from the centre of earth.
View Solution
Knowledge Check
The dependence of acceleration due to gravity g on the distance r from the centre of the earth, assumed to be a sphere of radius R of uniform density is as shown in Fig. below:
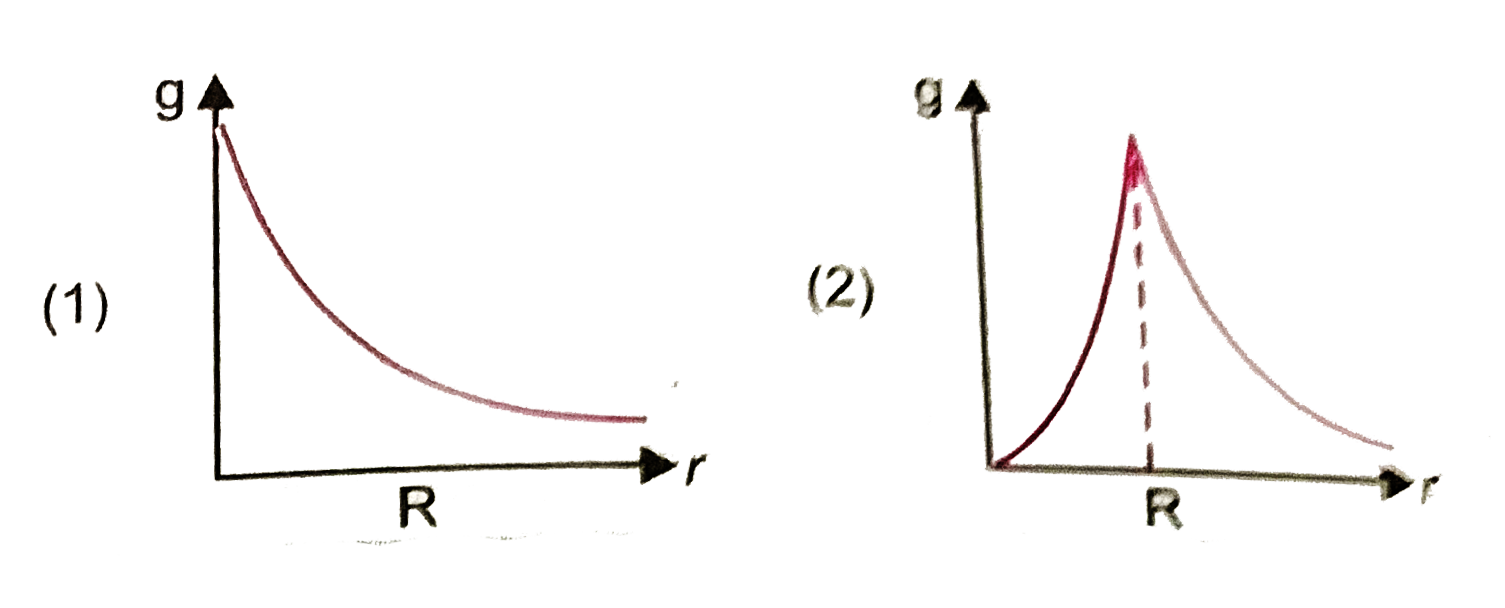
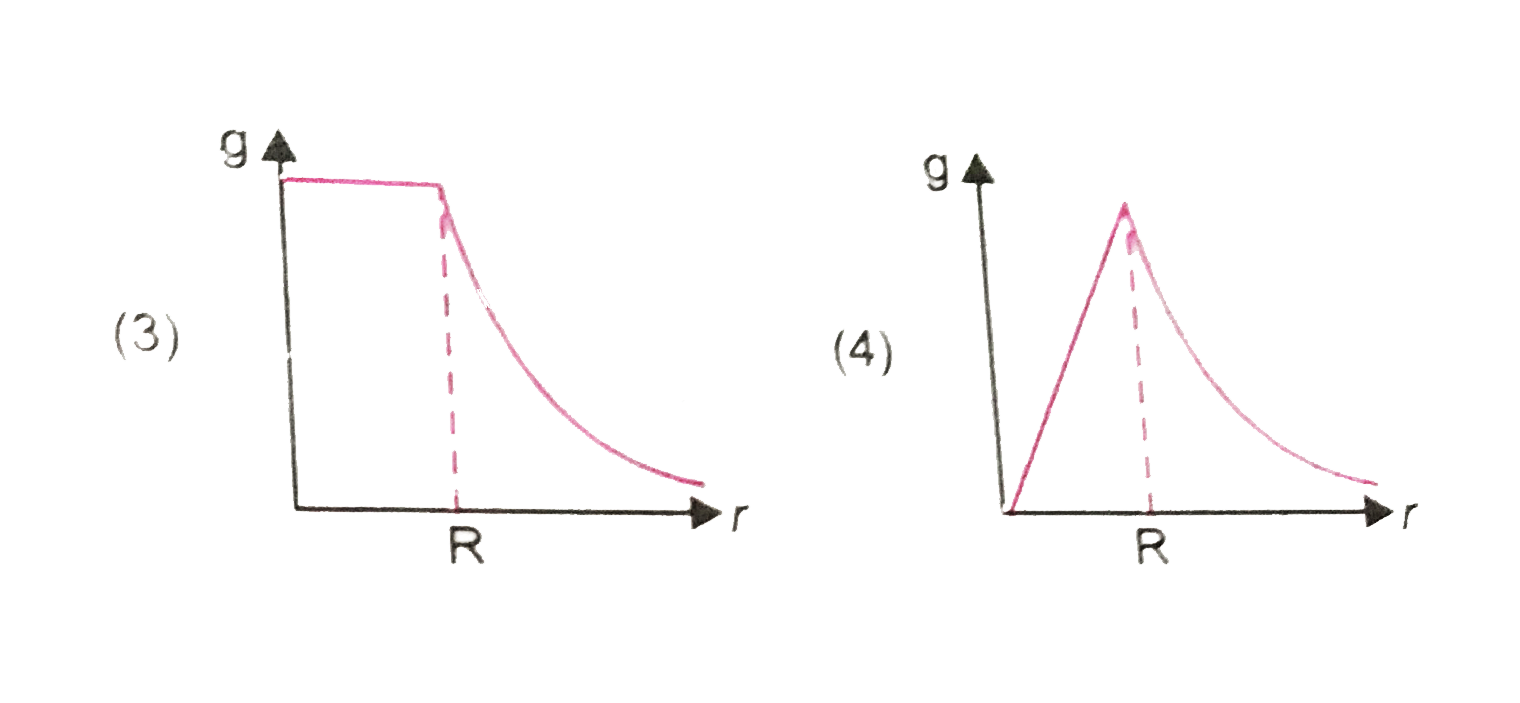
The correct figure isA(i)B(ii)C(iii)D(iv)
Assuming earth to be a sphere of uniform mass density, how much would a body weigh half way down the centre of the earth, if it weighed 100 N on the surface ?
View SolutionAssuming the earth to be a sphere of uniform mass density, how much would a body weigh half way down to the centre of the earth if it weighd 250 N on the surface ?
View SolutionAssuming earth to be a sphere of uniform mass density, how much would a body weigh half way down the center of the center of the earth , if it weighed 100 N on the surface?
View SolutionA tunnel is dug along a diameter of the earth. Find the force in on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionAssume that a tunnel is dug through earth from North pole to south pole and that the earth is a non-rotating, uniform sphere of density ρ. The gravitational force on a particle of mass m dropped into the tunnel when it reaches a distance r from the centre of earth is
View SolutionA tunnel is dug across the diameter of earth. A ball is released from the surface of Earth into the tunnel. The velocity of ball when it is at a distance R2 from centre of earth is (where R = radius of Earth and M = mass of Earth)
View Solutiona narrow tunnel is dug along the diameter of the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle from that place.

View Solution
