Three particle of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:A, B, C

To find the work done to increase the sides of an equilateral triangle from length $a$ to $2 a$ for three particles of mass $m$ each located at the corners, we can follow these steps:
Step 1: Calculate the Initial Potential Energy
The potential energy $U$ of a system of particles due to gravitational interaction is given by the formula:
$U = - \frac{G m_{1} m_{2}}{r}$
For three particles at the corners of an equilateral triangle with side $a$ , the potential energy of the system can be calculated as follows:
The potential energy between each pair of particles is:
- Between particle 1 and 2: $U_{12} = - \frac{G m^{2}}{a}$
- Between particle 2 and 3: $U_{23} = - \frac{G m^{2}}{a}$
- Between particle 3 and 1: $U_{31} = - \frac{G m^{2}}{a}$
Thus, the total initial potential energy $U_{i}$ is:
$U_{i} = U_{12} + U_{23} + U_{31} = - \frac{G m^{2}}{a} - \frac{G m^{2}}{a} - \frac{G m^{2}}{a} = - \frac{3 G m^{2}}{a}$
Step 2: Calculate the Final Potential Energy
When the sides of the triangle are increased to $2 a$ , we need to calculate the new potential energy $U_{f}$ :
The potential energy between each pair of particles is now:
- Between particle 1 and 2: $U_{12} = - \frac{G m^{2}}{2 a}$
- Between particle 2 and 3: $U_{23} = - \frac{G m^{2}}{2 a}$
- Between particle 3 and 1: $U_{31} = - \frac{G m^{2}}{2 a}$
Thus, the total final potential energy $U_{f}$ is:
$U_{f} = U_{12} + U_{23} + U_{31} = - \frac{G m^{2}}{2 a} - \frac{G m^{2}}{2 a} - \frac{G m^{2}}{2 a} = - \frac{3 G m^{2}}{2 a}$
Step 3: Calculate the Work Done
The work done $W$ on the system to increase the sides of the triangle is equal to the change in potential energy:
$W = U_{f} - U_{i}$
Substituting the values we found:
$W = (- \frac{3 G m^{2}}{2 a}) - (- \frac{3 G m^{2}}{a})$
This simplifies to:
$W = - \frac{3 G m^{2}}{2 a} + \frac{3 G m^{2}}{a} = - \frac{3 G m^{2}}{2 a} + \frac{6 G m^{2}}{2 a} = \frac{3 G m^{2}}{2 a}$
Final Answer
Thus, the work done on the system to increase the sides of the triangle to $2 a$ is:
$W = \frac{3 G m^{2}}{2 a}$
---

Updated on:18/9/2024

|

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Three point masses each of mass m are placed at the corners of an equilateral triangle of side b. The moment of inertia of the system about an axis coinciding with one side of the triangle is

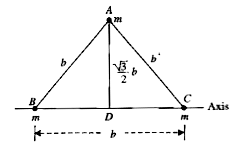A $3 m b^{2}$
B $m b^{2}$
C $(3 / 4) m b^{2}$
D $(2 / 3) m b^{2}$

DC PANDEY ENGLISH-GRAVITATION-Level 2 Subjective

Home
Ask Doubt
Profile