Question

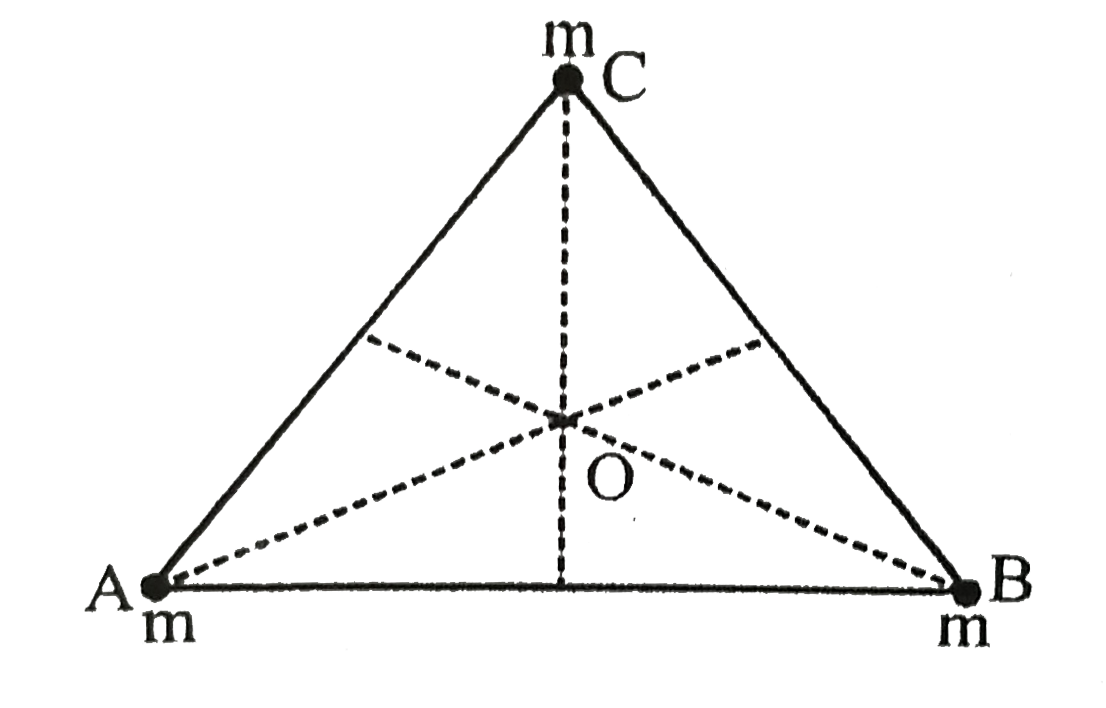
Three equal masses m are placed at the three corners of an equilateral triangle of side a. find the force exerted by this system on another particle of mass m placed at (a) the mid point of a side (b) at the center of the triangle.

Answer

A::B::C::D

Explanation

To solve the problem, we need to find the gravitational force exerted on a mass $$m$$ placed at (a) the midpoint of a side of an equilateral triangle formed by three equal masses $$m$$ at its corners, and (b) at the center of the triangle.

Part (a): Force at the Midpoint of a Side

1. Identify the Configuration:
- Let the three masses be located at points A, B, and C of the equilateral triangle with side length \( a \).
- The midpoint of side BC is denoted as point O.

2. Calculate the Distances:
- The distance from point O to point B (or C) is \( \frac{a}{2} \).
- The distance from point O to point A can be calculated using the height of the triangle. The height \( h \) of the triangle can be given by:
\( h = \frac{\sqrt{3}}{2} a \)
- Therefore, the distance from O to A is:
\( OA = h = \frac{\sqrt{3}}{2} a \)

3. Calculate the Forces:
- The gravitational force exerted on mass \( m \) at point O by mass at A:
\( F_{OA} = \frac{G m^2}{\left(\frac{\sqrt{3}}{2} a\right)^2} = \frac{G m^2}{\frac{3}{4} a^2} = \frac{4G m^2}{3a^2} \)
- The gravitational force exerted on mass \( m \) at point O by mass at B:
\( F_{OB} = \frac{G m^2}{\left(\frac{a}{2}\right)^2} = \frac{G m^2}{\frac{1}{4} a^2} = \frac{4G m^2}{a^2} \)
- The gravitational force exerted on mass \( m \) at point O by mass at C is the same as that from B:
\( F_{OC} = \frac{4G m^2}{a^2} \)

4. Net Force Calculation:
- The forces \( F_{OB} \) and \( F_{OC} \) are equal in magnitude but opposite in direction, thus they cancel each other out.
- Therefore, the net force on mass \( m \) at point O is:
\( F_{\text{net}} = F_{OA} + F_{OB} + F_{OC} = \frac{4G m^2}{3a^2} + 0 = \frac{4G m^2}{3a^2} \)

Part (b): Force at the Center of the Triangle

1. Identify the Center:
- The center of the triangle (centroid) is equidistant from all three masses. The distance from the centroid to any vertex (A, B, or C) is given by:
\( r = \frac{a}{\sqrt{3}} \)

2. Calculate the Forces:
- The gravitational force exerted on mass \( m \) at the centroid by mass at A:
\( F_{OA} = \frac{G m^2}{\left(\frac{a}{\sqrt{3}}\right)^2} = \frac{G m^2}{\frac{a^2}{3}} = \frac{3G m^2}{a^2} \)
- The forces from masses at B and C will be the same:
\( F_{OB} = F_{OC} = \frac{3G m^2}{a^2} \)

3. Net Force Calculation:
- Since the forces \( F_{OA} \), \( F_{OB} \), and \( F_{OC} \) are equal in magnitude but directed towards the centroid, they will cancel each other out.
- Therefore, the net force on mass \( m \) at the centroid is:
\( F_{\text{net}} = F_{OA} + F_{OB} + F_{OC} = 0 \)

Summary of Results:
- (a) The force exerted by the system on mass \( m \) at the midpoint of a side is \( \frac{4G m^2}{3a^2} \).
- (b) The force exerted by the system on mass \( m \) at the center of the triangle is \( 0 \).