If T be the period of revolution of a plant revolving around sun in an orbit of mean radius R, then identify the incorrect graph.
(d) None of these
The correct Answer is:D
To solve the problem, we need to analyze the relationship between the period of revolution T of a planet and the mean radius R of its orbit around the Sun, based on Kepler's Third Law of Planetary Motion.
1. Understanding Kepler's Third Law:
- According to Kepler's Third Law, the square of the period of revolution T of a planet is directly proportional to the cube of the mean radius R of its orbit.
- Mathematically, this can be expressed as:
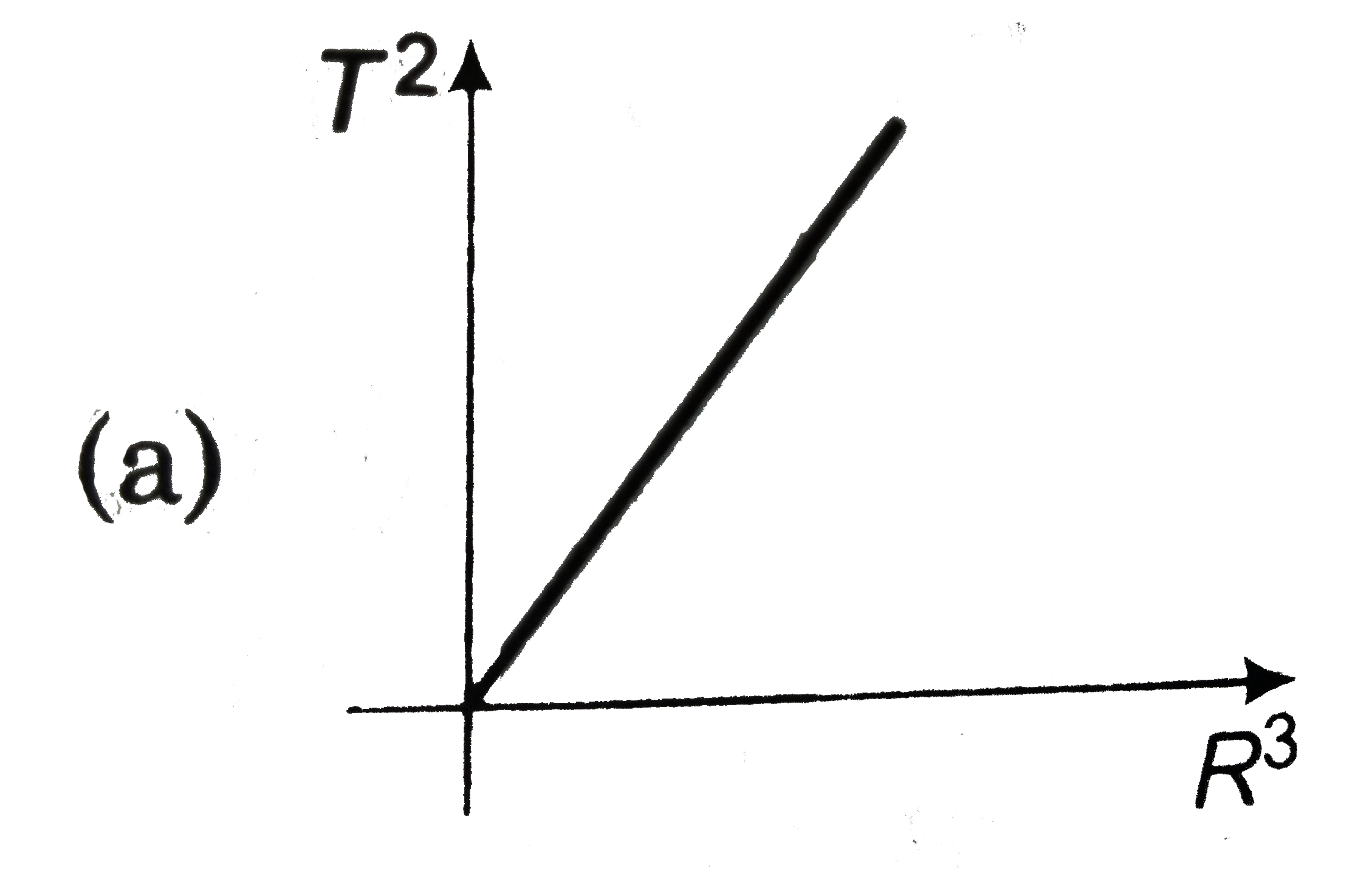
T2∝R3
- This implies:
T2=kR3
where k is a constant.
2. Identifying the Relationship:
- From the equation T2=kR3, we can derive that:
T2=kR3⟹T2=k(R3)
- This indicates that if we plot T2 against R3, we should get a straight line, which confirms that graph A is correct.
3. Analyzing Graph B:
- If we take the cube root of both sides from T2=kR3, we get:
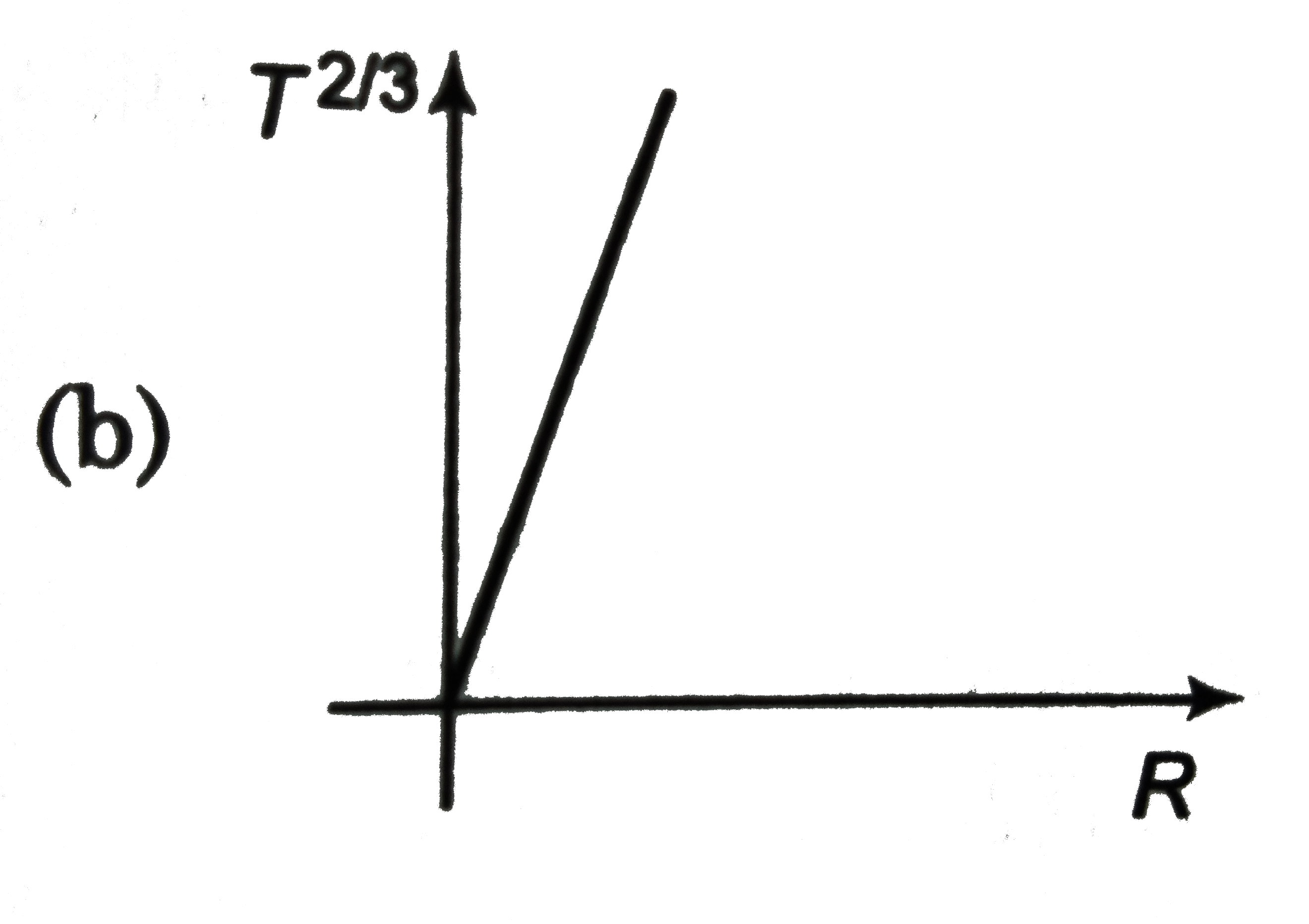
T2/3∝R
- This means that if we plot T2/3 against R, we should also obtain a linear relationship, confirming that graph B is correct.
4. Analyzing Graph C:
- Now, if we consider the relationship between T2 and 1R3:
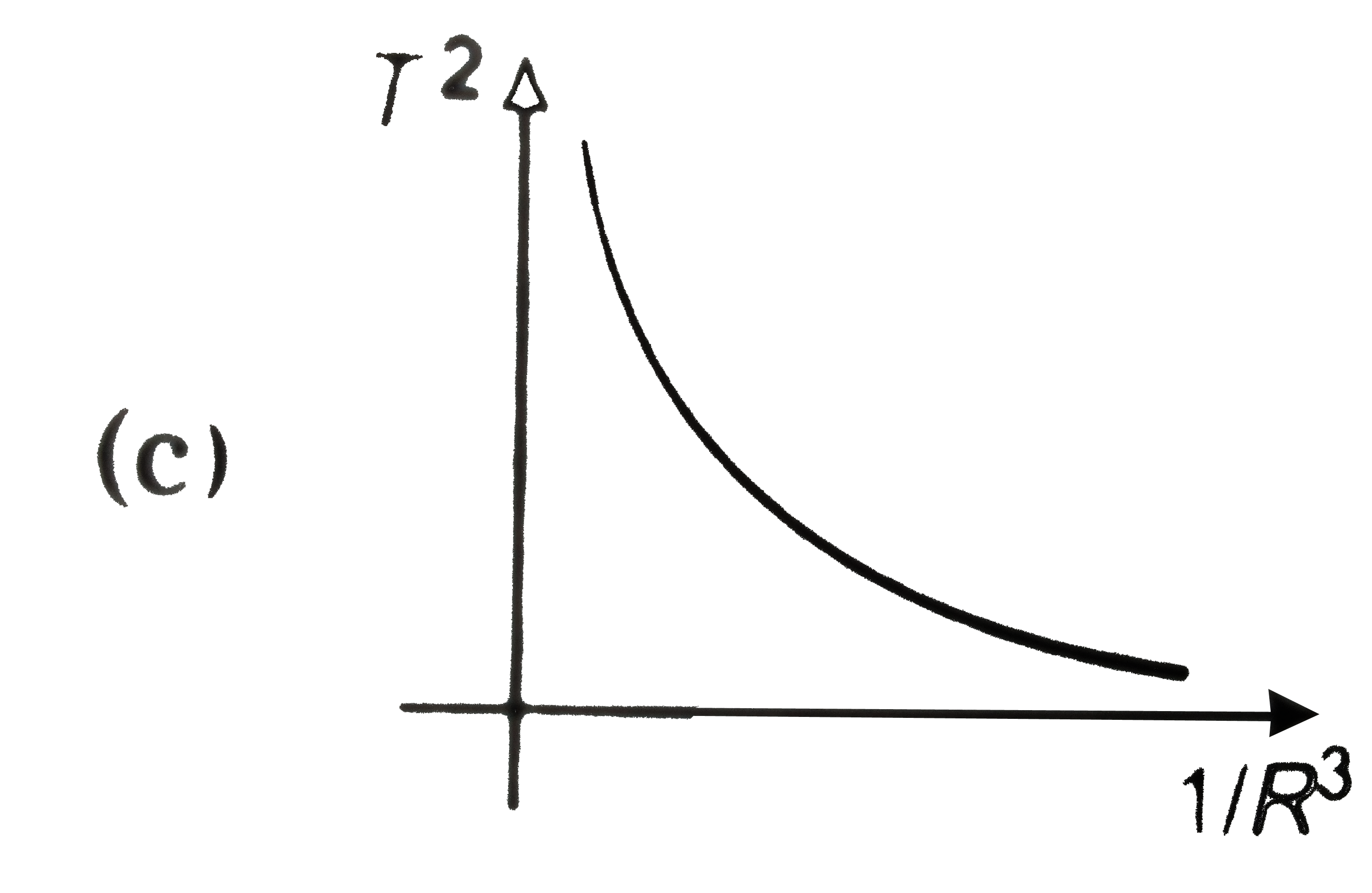
T2∝R3⟹T2∝11R3
- This implies that if we plot T2 against 1R3, we should expect a rectangular hyperbola, which is not a linear relationship. Therefore, graph C is incorrect.
5. Conclusion:
- Based on the analysis of the relationships derived from Kepler's Third Law, we conclude that graph C is the incorrect graph.
Final Answer:
The incorrect graph is Graph C.
- According to Kepler's Third Law, the square of the period of revolution T of a planet is directly proportional to the cube of the mean radius R of its orbit.
- Mathematically, this can be expressed as:
T2∝R3
- This implies:
T2=kR3
where k is a constant.
- From the equation T2=kR3, we can derive that:
T2=kR3⟹T2=k(R3)
- This indicates that if we plot T2 against R3, we should get a straight line, which confirms that graph A is correct.
- If we take the cube root of both sides from T2=kR3, we get:
T2/3∝R
- This means that if we plot T2/3 against R, we should also obtain a linear relationship, confirming that graph B is correct.
- Now, if we consider the relationship between T2 and 1R3:
T2∝R3⟹T2∝11R3
- This implies that if we plot T2 against 1R3, we should expect a rectangular hyperbola, which is not a linear relationship. Therefore, graph C is incorrect.
- Based on the analysis of the relationships derived from Kepler's Third Law, we conclude that graph C is the incorrect graph.
The incorrect graph is Graph C.
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 More Than One Correct
10 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 Subjective
14 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 1 Subjective
19 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Identify the incorrect statement about a planet revolving around Sun
View SolutionFor a planet revolving around Sun in an elliptical orbit, to obtain its velocity at any point we have to apply
View SolutionAssertion (A) : The time period of revolution of a satellite around a planet is directly proportional to the radius of the orbit of the satellite.
Reason (R) : Artifical satellite do not follow Kepler's laws of planatory motion.
View SolutionThe period of revolution of a satellite in an orbit of radius 2R is T. What will be its period of revolution in an orbit of radius 8R ?
View SolutionIf L is the angular momentum of a satellite revolving around earth is a circular orbit of radius r with speed v , then
View SolutionKepler's law starts that square of the time period of any planet moving around the sun in an elliptical orbit of semi-major axis (R) is directly proportional to
View Solutiontwo electron are revolving around a nucleus at distance rand4 r. The ratio of their periods is
View SolutionA planet is revolving around the sun. its distance from the sun at apogee is rA and that at perigee is rp. The masses of planet and sun are 'm' and M respectively, VA is the velocity of planet at apogee and VP is at perigee respectively and T is the time period of revolution of planet around the sun, then identify the wrong answer.
View SolutionFind the period of revolution of a satellite revolving the earth at a height of 200km above earth's surface ? Radius of earth = 6400 km
View SolutionA satellite is revolving round the earth in an orbit of radius r with time period T. If the satellite is revolving round the earth in an orbit of radius r+Δr(Δr<<r) with time period T+ΔT(ΔT<<T) then.
View Solution
