Find the maximum and minimum distances of the planet A from the sun S, if at a certain moment of times it was at a distance r0 and travelling with the velocity υ0. With the angle between the radius vector and velocity vector being equal to ϕ.
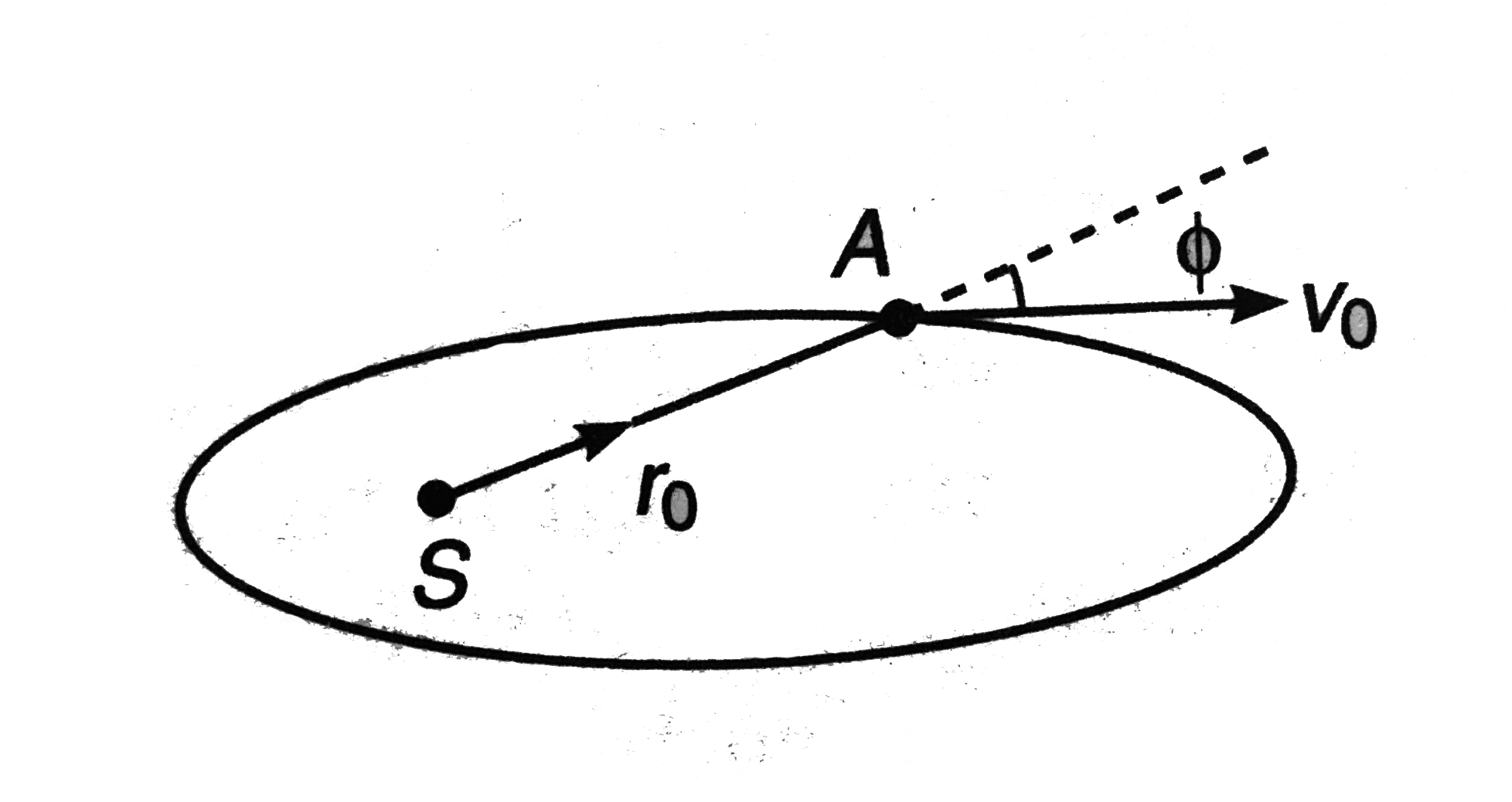
At minimum and maximum distance velocity vector (V) makes an angle of 90∘ with radius vector. Hence, from conservation of angular momentum,
μυ0r0sinϕ=mrυ ..(i)
Hence, m is the mass of the plant.
From energy conservation law, it follows that
mυ202−GMmr0=mυ22−GMmr ..(ii)
Hence, M is the mass of the sun.
Solving Eqs. (i) and (ii) for r, we fet two values of r, one is rmax and another is rmin. So,
rmax=r02−K(1+√1−K(2−K)sin2ϕ)
and rmin=r02−K(1−√1−K(2−K)sin2ϕ)
Here, K=r20υ20GM
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Miscellaneous Examples
8 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 13.1
5 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
A planet A moves along an elliptical orbit around the Sun. At the moment when it was at the distance r0 from the Sun its velocity was equal to v0 and the angle between the radius vector r0 and the velocity vector v0 was equal to α. Find the maximum and minimum distances that will separate this planet from the Sun during its orbital motion.
View SolutionThe ratio of mean distances of three planets from the sun are 0.5:1:1:5, then the square of time periods are in the ratio of
View SolutionThe minimum and maximum distances of a planet revolving around sun are r and R . If the minimum speed of planet of its trajectory is v0 , its maximum speed will be
View SolutionThe maximum and minimum distance of a comet form the sun are 8×1012mand1.6×1012m. If its velocity when nearest to the sun is 60m/s, what will be its velocity in m/s when it is farthest
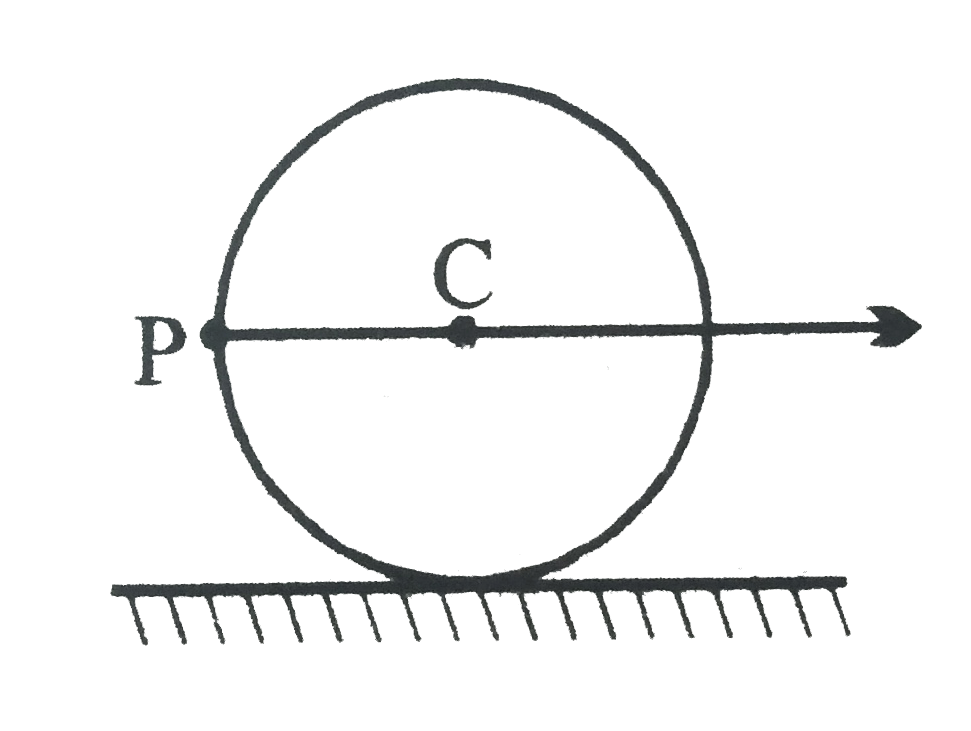
View SolutionA disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity and acceleration vectors of point P is
 .
.
View Solution
A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity the angle between the velocity ad acceleration vectors of point P is
View SolutionThe minimum and maximum distance of a satellite from the centre of the earth are 2R and 4R respectively, where R is the radius of earth and M is the mass of the earth. The radius of curvature at the point of maximum distance is
View SolutionThe minimum and maximum distances of a satellite from the center of the earth are 2R and 4R respectively, where R is the radius of earth and M is the mass of the earth . Find
(a) its minimum and maximum speeds,
(b) radius of curvature at the point of minimum distance.
View SolutionA planet is revolving around the Sun in an elliptical orbit. Its closest distance from the sun is rmin. The farthest distance from the sun is rmax if the orbital angular velocity of the planet when it is nearest to the Sun ω then the orbital angular velocity at the point when it is at the farthest distance from the sun is
View SolutionThe maximum and minimum distances of a cornet form Sun are 1.4×1012mand7×1010m. If velocity nearest to Sun is 6×104ms−1, what is velocity if cornet when it is farthest from the Sun ?
View Solution
