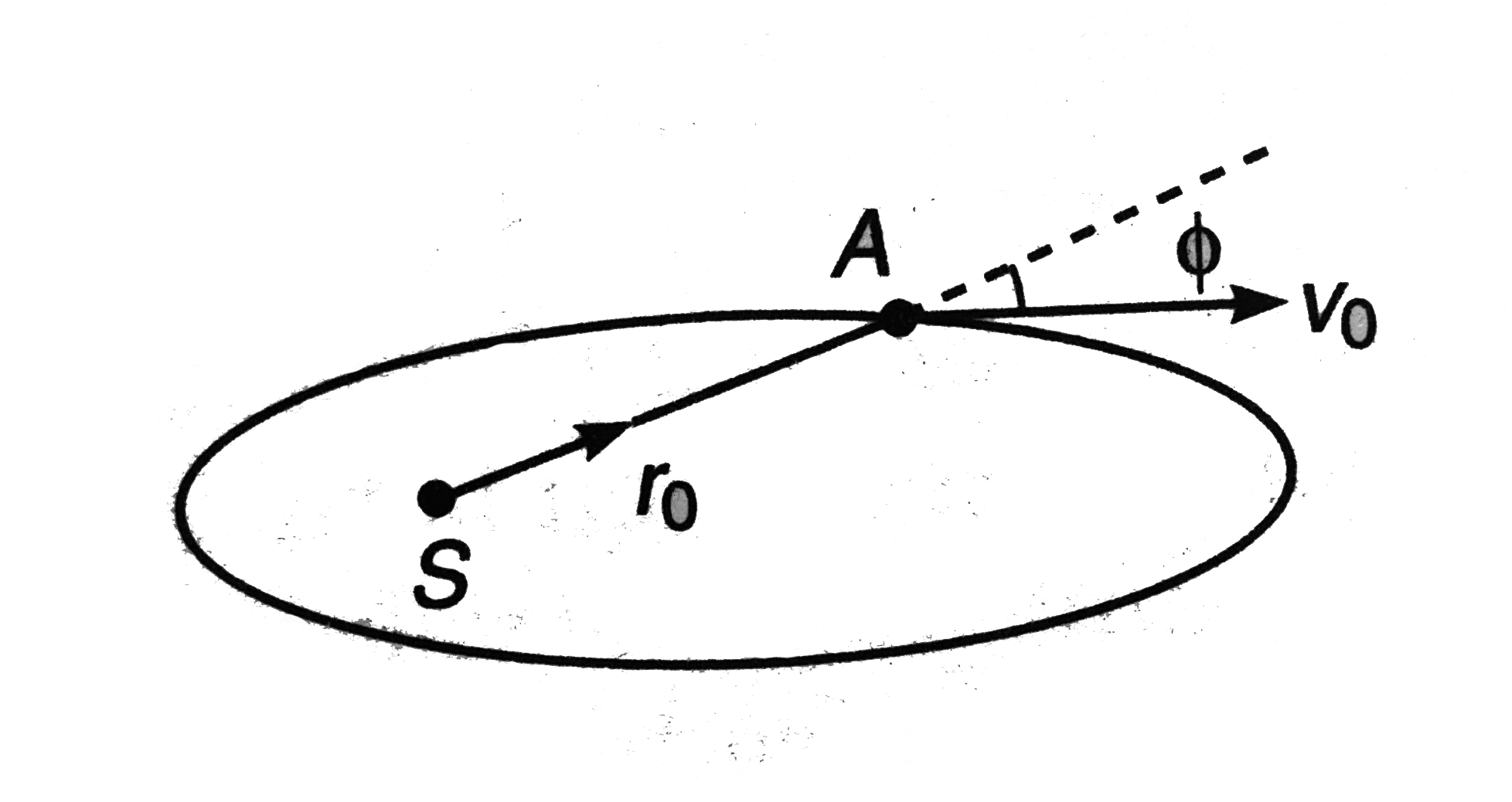
A planet A moves along an elliptical orbit around the Sun. At the moment when it was at the distance $r_{0}$ from the Sun its velocity was equal to $v_{0}$ and the angle between the radius vector $r_{0}$ and the velocity vector $v_{0}$ was equal to $α$ . Find the maximum and minimum distances that will separate this planet from the Sun during its orbital motion.

Video Solution

Text Solution

Generated By DoubtnutGPT

To find the maximum and minimum distances that will separate the planet A from the Sun during its orbital motion, we can follow these steps:
Step 1: Understand the problem
We have a planet A moving in an elliptical orbit around the Sun. At a certain point, it is at a distance $r_{0}$ from the Sun with a velocity $v_{0}$ and an angle $α$ between the radius vector $r_{0}$ and the velocity vector $v_{0}$ .
Step 2: Conservation of Angular Momentum
The angular momentum $L$ of the planet at the distance $r_{0}$ is given by:
$L = m v_{0} r_{0} sin (α)$
where $m$ is the mass of the planet. Since angular momentum is conserved, we can express it at the maximum distance $r_{1}$ and minimum distance $r_{2}$ as:
$L = m v_{1} r_{1} = m v_{2} r_{2}$
where $v_{1}$ and $v_{2}$ are the velocities at distances $r_{1}$ and $r_{2}$ , respectively.
Step 3: Relate velocities and distances
From the conservation of angular momentum, we can write:
$v_{0} r_{0} sin (α) = v_{1} r_{1} = v_{2} r_{2}$
This gives us:
$v_{1} = \frac{v_{0} r_{0} sin (α)}{r_{1}} and v_{2} = \frac{v_{0} r_{0} sin (α)}{r_{2}}$
Step 4: Conservation of Mechanical Energy
The total mechanical energy $E$ at distance $r_{0}$ is given by the sum of kinetic energy $K$ and gravitational potential energy $U$ :
$E = K + U = \frac{1}{2} m v_{0}^{2} - \frac{G M m}{r_{0}}$
At distances $r_{1}$ and $r_{2}$ , we have:
$E = \frac{1}{2} m v_{1}^{2} - \frac{G M m}{r_{1}} and E = \frac{1}{2} m v_{2}^{2} - \frac{G M m}{r_{2}}$
Step 5: Set up the energy equations
Setting the energy equations equal to each other, we have:
$\frac{1}{2} m v_{0}^{2} - \frac{G M m}{r_{0}} = \frac{1}{2} m v_{1}^{2} - \frac{G M m}{r_{1}}$
and
$\frac{1}{2} m v_{0}^{2} - \frac{G M m}{r_{0}} = \frac{1}{2} m v_{2}^{2} - \frac{G M m}{r_{2}}$
Step 6: Substitute for $v_{1}$ and $v_{2}$
Substituting the expressions for $v_{1}$ and $v_{2}$ into the energy equations, we can derive two equations involving $r_{1}$ and $r_{2}$ .
Step 7: Formulate quadratic equations
After substituting and rearranging, we will arrive at two quadratic equations in terms of $r_{1}$ and $r_{2}$ .
Step 8: Solve the quadratic equations
Using the quadratic formula:
$r = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
we can find the values for $r_{1}$ and $r_{2}$ .
Final Results
The maximum distance $r_{1}$ and minimum distance $r_{2}$ can be expressed as:
$r_{1} = expression involving r_{0}, v_{0}, α, G, M$
$r_{2} = expression involving r_{0}, v_{0}, α, G, M$

Updated on:18/9/2024

|

Class 12 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

A planet is revolving in an elliptical orbit around the sun. Its closest distance from the sun is r and the farthest distance is R. If the velocity of the planet nearest to the sun be v and that farthest away from the sun be V. then v/V is
A $R^{2} / r^{2}$
B $r^{2} / R^{2}$
C $R / r$
D $r / R$

AAKASH INSTITUTE ENGLISH-GRAVITATION -ASSIGNMENT SECTION -J (Aakash Challengers Questions)

Home
Ask Doubt
Profile