In the problem discussed in the text, find the values of E and V at p dua to the remaining mass.
The correct Answer is:A, B, C, D
To find the gravitational field E and gravitational potential V at point P due to the remaining mass, we will follow these steps:
Step 1: Determine the mass of the cavity
The mass of the cavity can be calculated using the formula for the volume of a sphere and the density ρ:
Mass of cavity=ρ×Volume of cavity=ρ×(43π(R4)3)
Calculating this gives:
Mass of cavity=ρ×43π×R364=ρπR348
Step 2: Determine the mass of the solid sphere without the cavity
The mass of the solid sphere can be calculated similarly:
Mass of solid sphere=ρ×(43πR3)=43πR3ρ
Let’s denote this mass as M.
Step 3: Calculate the gravitational field E
The total gravitational field E at point P is the sum of the gravitational fields due to the solid sphere and the cavity:
E=Esolid−Ecavity
Where:
- Esolid=−GM(3R)2^i
- Ecavity=−G(ρπR348)(9R4)2^i
Calculating these values:
Esolid=−G(43πR3ρ)9R2^i=−4GπRρ27^i
Ecavity=−G(ρπR348)(9R4)2=−G(ρπR348)81R216=−16GρπR3888
Step 4: Combine the gravitational fields
Now, substituting these values into the equation for E:
E=−4GπRρ27+16GρπR3888
Step 5: Calculate the gravitational potential V
The gravitational potential V at point P is given by:
V=Vsolid−Vcavity
Where:
- Vsolid=−GM3R
- Vcavity=−G(ρπR348)9R4
Calculating these values:
Vsolid=−G(43πR3ρ)3R=−4GπR2ρ9
Vcavity=−G(ρπR348)9R4=−4GρπR2432
Step 6: Combine the gravitational potentials
Now, substituting these values into the equation for V:
V=−4GπR2ρ9+4GρπR2432
Final Values
After performing the calculations, we find:
- Gravitational field E at point P
- Gravitational potential V at point P
The mass of the cavity can be calculated using the formula for the volume of a sphere and the density ρ:
Mass of cavity=ρ×Volume of cavity=ρ×(43π(R4)3)
Calculating this gives:
Mass of cavity=ρ×43π×R364=ρπR348
The mass of the solid sphere can be calculated similarly:
Mass of solid sphere=ρ×(43πR3)=43πR3ρ
Let’s denote this mass as M.
The total gravitational field E at point P is the sum of the gravitational fields due to the solid sphere and the cavity:
E=Esolid−Ecavity
Where:
- Esolid=−GM(3R)2^i
- Ecavity=−G(ρπR348)(9R4)2^i
Esolid=−G(43πR3ρ)9R2^i=−4GπRρ27^i
Ecavity=−G(ρπR348)(9R4)2=−G(ρπR348)81R216=−16GρπR3888
Now, substituting these values into the equation for E:
E=−4GπRρ27+16GρπR3888
The gravitational potential V at point P is given by:
V=Vsolid−Vcavity
Where:
- Vsolid=−GM3R
- Vcavity=−G(ρπR348)9R4
Vsolid=−G(43πR3ρ)3R=−4GπR2ρ9
Vcavity=−G(ρπR348)9R4=−4GρπR2432
Now, substituting these values into the equation for V:
V=−4GπR2ρ9+4GρπR2432
After performing the calculations, we find:
- Gravitational field E at point P
- Gravitational potential V at point P
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Miscellaneous Examples8videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 13.15videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE10videos
KINEMATICS
Similar Questions
F∈dthevalueofp
View SolutionIn the problem discussed in the text, find E−r expressions for inside and outside points.
View SolutionA small section of area ΔA is removed from a uniform spherical shell with surface mass density σ and radius R as shown in the figure . Find the magnitude of gravitational field intensity at point P due to the remaining mass .
 View Solution
View SolutionA uniform rod AB of length L and mass M is lying on a smooth table. A small particle if mass m strike the rod with velocity v0 at point C at a distance comes to rest after collision. Then find the value of x, so that point A of the rod remains stationary just after collision.
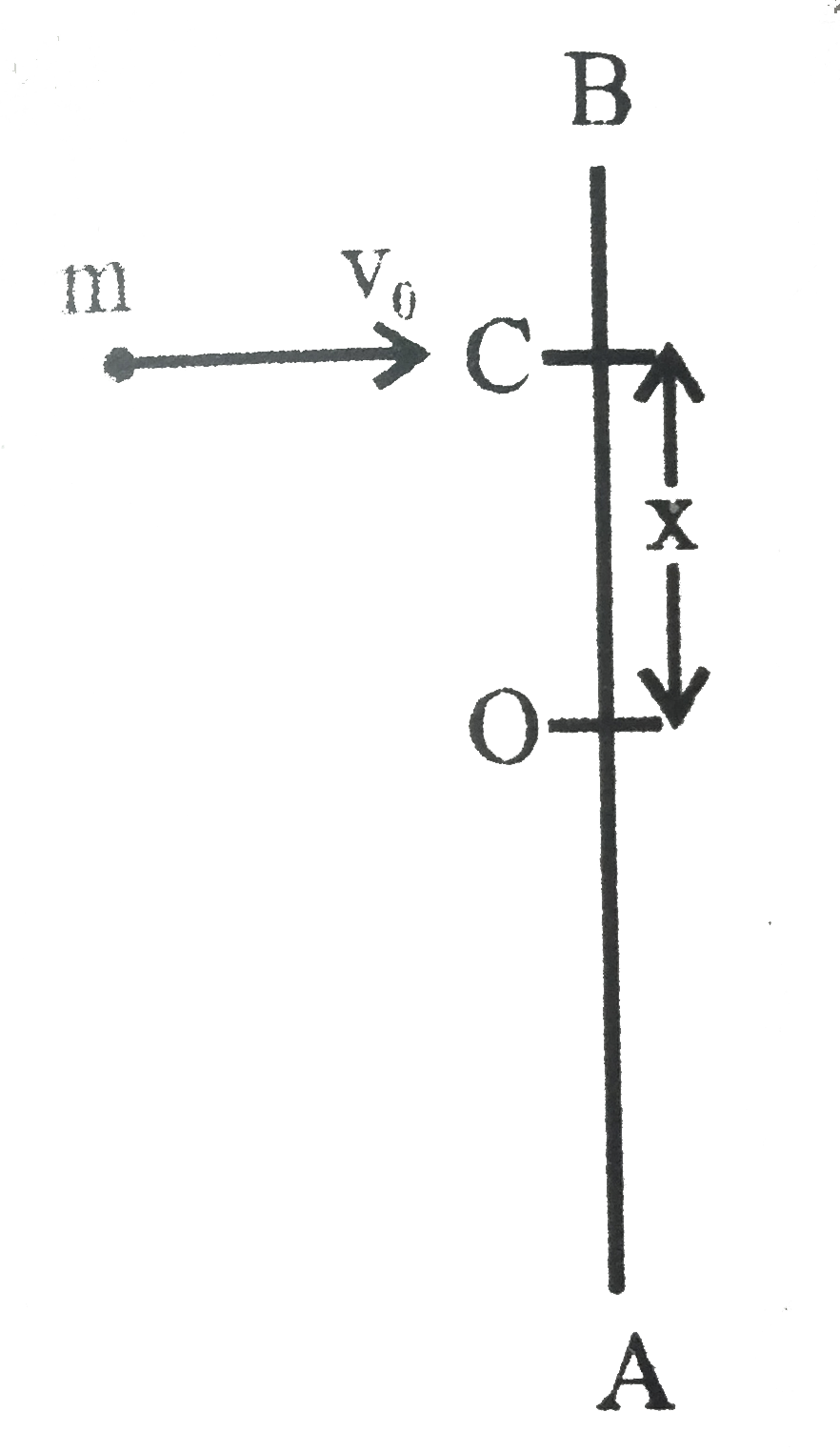 .View Solution
.View SolutionIf a,b,c,d,e are in A.P., the find the value of a−4b+6c−4d+e.
View SolutionIn previous, Find the value of γ=CP/Cv:
View SolutionA particle of mass m is projected upwards with velocity v=ve2, where ve is the escape velocity then at the maximum height the potential energy of the particle is : (R is radius of earth and M is mass of earth)
View SolutionFind the potential V at P in the gravitational field of fixed point mass M.
View SolutionIf E' denote the complement of an event E , what is the value of P(E')+P(E)?
View SolutionSuppose the 19Ω resistor of the previous problem is disconnected. Find the current through P2Q2 in the two situations (a) and (b) of that problem.
View Solution
