The ratio of mean distances of three planets from the sun are 0.5:1:1:5, then the square of time periods are in the ratio of
1:4:9
1:9:4
1:8:27
2:1:3
The correct Answer is:C
To solve the problem, we will use Kepler's Third Law of Planetary Motion, which states that the square of the time period (T) of a planet is directly proportional to the cube of the mean distance (R) from the sun. Mathematically, this can be expressed as:
T2∝R3
Given the ratio of the mean distances of the three planets from the sun as 0.5:1:1.5, we will denote these distances as:
- R1=0.5
- R2=1
- R3=1.5
Step 1: Calculate the cube of the distances
We need to calculate the cube of each distance:
1. R31=(0.5)3=0.125
2. R32=(1)3=1
3. R33=(1.5)3=3.375
Step 2: Write the ratios of the cubes
Now we can express the ratios of the cubes of the distances:
- The ratio of R31:R32:R33=0.125:1:3.375
Step 3: Simplify the ratio
To simplify this ratio, we can multiply each term by 8 (to eliminate the decimal):
- 0.125×8=1
- 1×8=8
- 3.375×8=27
Thus, the ratio becomes:
1:8:27
Step 4: Relate this back to the time periods
According to Kepler's law, since T2∝R3, we can write:
T21:T22:T23=R31:R32:R33
Therefore, the ratio of the squares of the time periods is:
T21:T22:T23=1:8:27
Final Answer
The square of the time periods are in the ratio 1:8:27.
---
- R2=1
- R3=1.5
We need to calculate the cube of each distance:
2. R32=(1)3=1
3. R33=(1.5)3=3.375
Now we can express the ratios of the cubes of the distances:
To simplify this ratio, we can multiply each term by 8 (to eliminate the decimal):
- 1×8=8
- 3.375×8=27
According to Kepler's law, since T2∝R3, we can write:
The square of the time periods are in the ratio 1:8:27.
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.2
20 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.3
15 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 Subjective
14 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
The distance of the two planets from the Sun are 1013m and 1012m, respectively. Find the ratio of time periods of the two planets.
View SolutionThe distance of the two planets from the Sun are 1013m and 1012m, respectively. Find the ratio of time periods of the two planets.
View SolutionThe ratio of distance of two satellites from the centre of earth is 1:4. The ratio of their time periods of rotation will be
View SolutionThe ratio of distance of two satellites from the centre of earth is 1:4. The ratio of their time periods of rotation will be
View SolutionA planet of mass m is moving in an elliptical orbit about the sun (mass of sun = M). The maximum and minimum distances of the planet from the sun are r1 and r2 respectively. The period of revolution of the planet wil be proportional to :
View SolutionA planet of mass m moves around the Sun of mass Min an elliptical orbit. The maximum and minimum distance of the planet from the Sun are r1 and r2, respectively. Find the relation between the time period of the planet in terms of r1 and r2.
View SolutionThe ratio of diameters of molecules of the two gases is 3:5 and their mean free path of the molecule is in the ratio of 5:3 then the ratio of number density of the two gases is
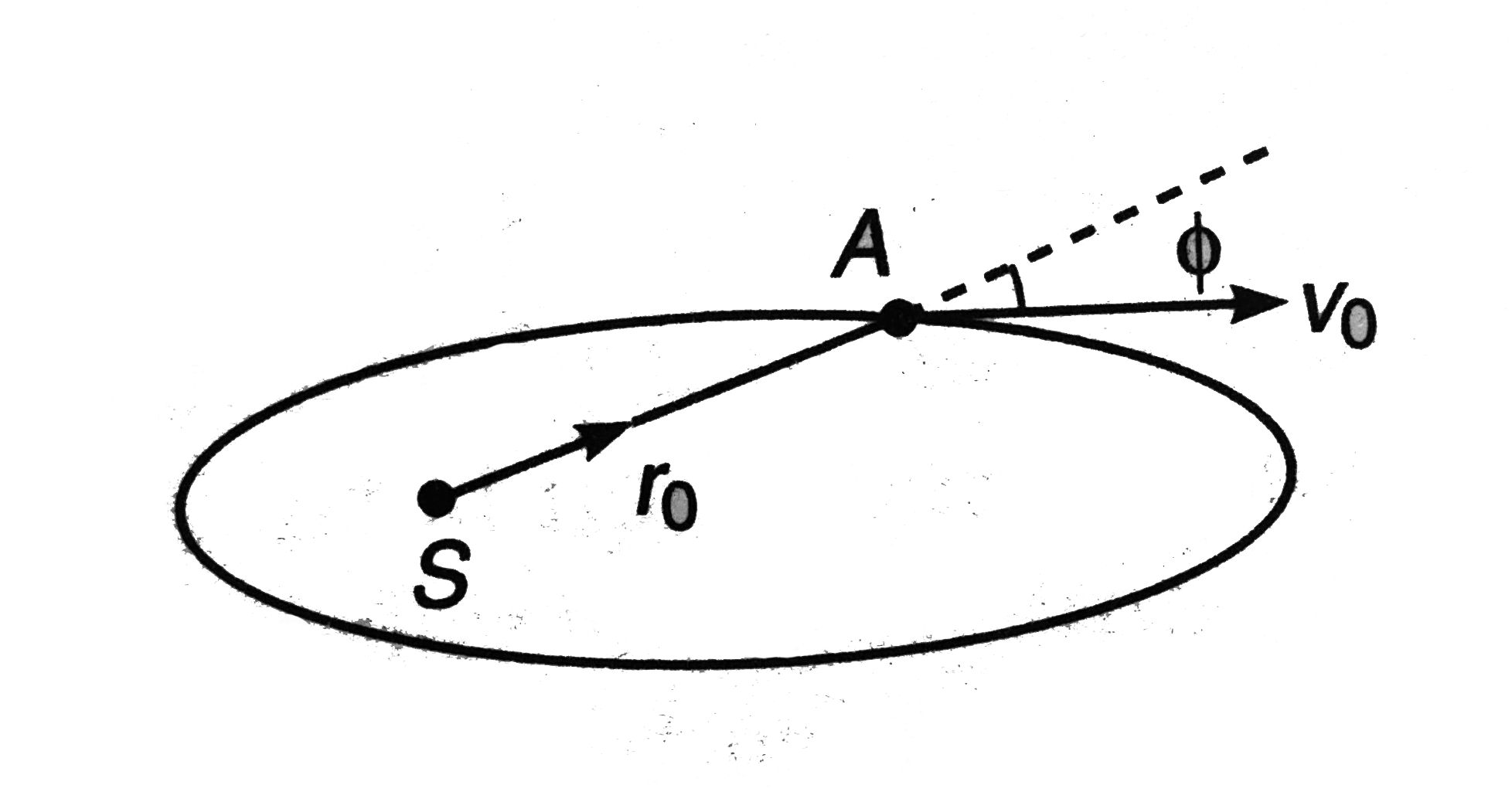
View SolutionFind the maximum and minimum distances of the planet A from the sun S, if at a certain moment of times it was at a distance r0 and travelling with the velocity υ0. With the angle between the radius vector and velocity vector being equal to ϕ.
View SolutionThe distance of the planet Jupiter from the Sun is 5.2 times that of the Earth. Find the period of Jupiter's revolution around the Sun.
View SolutionAstronomers observe two separate solar systems each consisting of a planet orbiting a sun. The two orbits are circular and have the same radius R. It is determined that the planets have angular momenta of the same magnitude L about their suns, and that the orbital periods are in the ratio of three to one, i.e. T1=3T2. The ratio m1/m2 of the masses of the two planets is
View Solution
