Astronomers observe two separate solar systems each consisting of a planet orbiting a sun. The two orbits are circular and have the same radius R. It is determined that the planets have angular momenta of the same magnitude L about their suns, and that the orbital periods are in the ratio of three to one, i.e. T1=3T2. The ratio m1/m2 of the masses of the two planets is
1
√3
2
3
The correct Answer is:D
To solve the problem, we need to find the ratio of the masses of two planets orbiting their respective suns, given that both planets have the same angular momentum and that their orbital periods are in the ratio of 3:1.
1. Understanding Angular Momentum:
The angular momentum L of a planet in a circular orbit is given by the formula:
L=m⋅v⋅r
where m is the mass of the planet, v is its orbital velocity, and r is the radius of the orbit.
2. Given Conditions:
- The radii of the orbits are the same: r1=r2=R.
- The angular momenta are equal: L1=L2.
- The periods are in the ratio T1=3T2.
3. Expressing Velocity:
The orbital velocity v can be expressed in terms of the radius and the period:
v=2πrT
Thus, for the two planets we have:
v1=2πRT1andv2=2πRT2
4. Substituting into Angular Momentum:
Now substituting the expressions for velocity into the angular momentum equations:
L1=m1⋅v1⋅R=m1⋅(2πRT1)⋅R=m1⋅2πR2T1
L2=m2⋅v2⋅R=m2⋅(2πRT2)⋅R=m2⋅2πR2T2
5. Setting Angular Momenta Equal:
Since L1=L2:
m1⋅2πR2T1=m2⋅2πR2T2
The 2πR2 cancels out:
m1⋅1T1=m2⋅1T2
6. Rearranging for Mass Ratio:
Rearranging gives:
m1m2=T1T2
7. Substituting the Period Ratio:
We know T1=3T2:
m1m2=3T2T2=3
Final Answer:
The ratio of the masses of the two planets is:
m1m2=3
The angular momentum L of a planet in a circular orbit is given by the formula:
L=m⋅v⋅r
where m is the mass of the planet, v is its orbital velocity, and r is the radius of the orbit.
- The radii of the orbits are the same: r1=r2=R.
- The angular momenta are equal: L1=L2.
- The periods are in the ratio T1=3T2.
The orbital velocity v can be expressed in terms of the radius and the period:
v=2πrT
Thus, for the two planets we have:
v1=2πRT1andv2=2πRT2
Now substituting the expressions for velocity into the angular momentum equations:
L1=m1⋅v1⋅R=m1⋅(2πRT1)⋅R=m1⋅2πR2T1
L2=m2⋅v2⋅R=m2⋅(2πRT2)⋅R=m2⋅2πR2T2
Since L1=L2:
m1⋅2πR2T1=m2⋅2πR2T2
The 2πR2 cancels out:
m1⋅1T1=m2⋅1T2
Rearranging gives:
m1m2=T1T2
We know T1=3T2:
m1m2=3T2T2=3
The ratio of the masses of the two planets is:
m1m2=3
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
Two satellites of masses M and 16 M are orbiting a planet in a circular orbitl of radius R. Their time periods of revolution will be in the ratio of
View SolutionIf the angular momentum of a planet of mass m, moving around the Sun in a circular orbit is L, about the center of the Sun, its areal velocity is :
View SolutionFigure shows the elipticla path of a planet about the sun. The two shaded parts have equal area. If t1andt2 be the tim taken by the planet to go from a to b and from c to d respectively
View SolutionA planet of mass m is in an elliptical orbit about the sun (m << Msun) with an orbital period T. If A be the area of orbit, then its angular momentum would be:
View SolutionTwo satellite of mass m and 9m are orbiting a planet in orbits of radius R. Their periods of revolution will be in the ratio of
View SolutionConsider a hypothetical solar system, which has two identical massive suns each of mass M and radius r, seperated by a seperation of 2√3R (centre to centre). (R>>r). These suns are always at rest. There is only one planet in this solar system having mass m. This planet is revolving in circular orbit of radius R such that centre of the orbit lies at the mid point of the line joining the centres of the sun and plane of the orbit is perpendicular to the line joining the centres of the sun. Whole situation is shown in the figure.
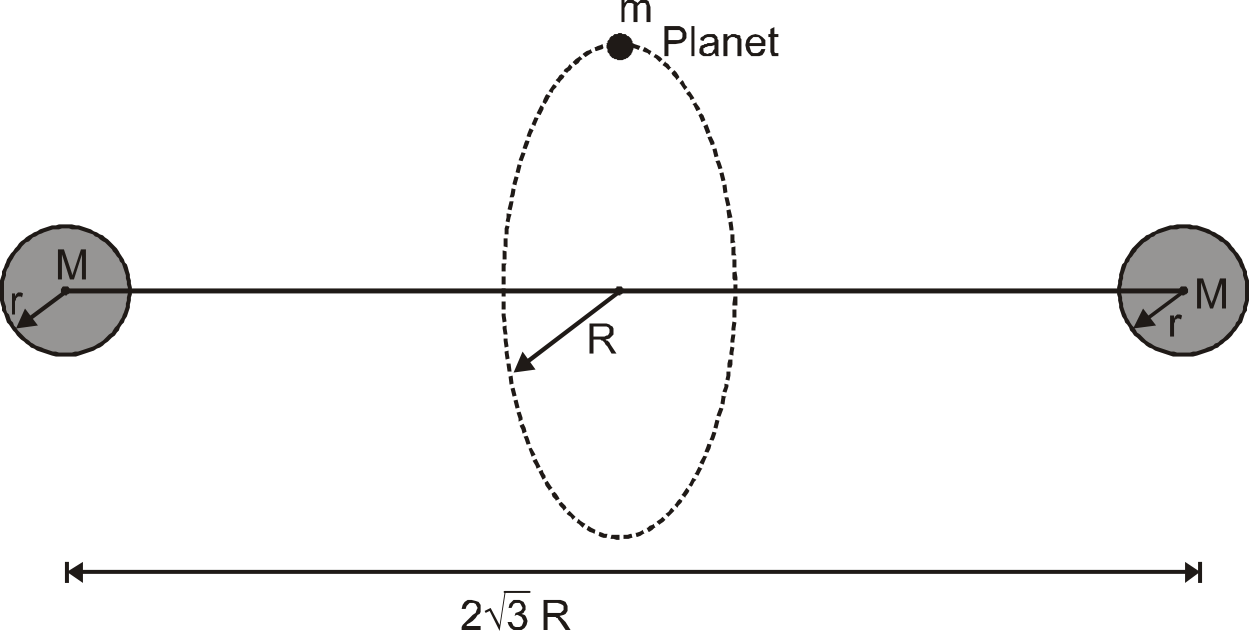
Q. Speed of the planet is
View SolutionConsider a hypothetical solar system, which has two identical massive suns each of mass M and radius r, seperated by a seperation of 2√3R (centre to centre). (R gtgtgtr). These suns are always at rest. There is only one planet in this solar system having mass m. This planet is revolving in circular orbit of radius R such that centre of the orbit lies at the mid point of the line joining the centres of the sun and plane of the orbit is perpendicular to the line joining the centres of the sun. Whole situation is shown in the figure.

Q. Average force on the planet in half revolution is
View SolutionTwo planets of same density have the ratio of their radii as 1 : 3. The ratio of escape speed on them will be
View SolutionA body is moving in a low circular orbit about a planet of mass M and radius R. The radius of the orbit can be taken to be R itself. Then the ratio of the speed of this body in the orbit to the escape velocity from the planet is :
View SolutionA small planet is revolving around a massive star in a circular orbit of radius R with a period of revolution T. If the gravitational force between the planet and the star were proportional to R−5/2, then T would be proportional to
View Solution
